给定两个正整数m=126和n=198,利用辗转相除算法,求它们的最小公倍数,并写出求解过程。
题目
相似考题
更多“给定两个正整数m=126和n=198,利用辗转相除算法,求它们的最小公倍数,并写出求解过程。”相关问题
-
第1题:
阅读以下说明和流程图,回答问题1-2,将解答填入对应的解答栏内。
[说明]
下面的流程图采用欧几里得算法,实现了计算两正整数最大公约数的功能。给定正整数m和 n,假定m大于等于n,算法的主要步骤为:
(1)以n除m并令r为所得的余数;
(2)若r等于0,算法结束;n即为所求;
(3)将n和r分别赋给m和n,返回步骤(1)。
[流程图]
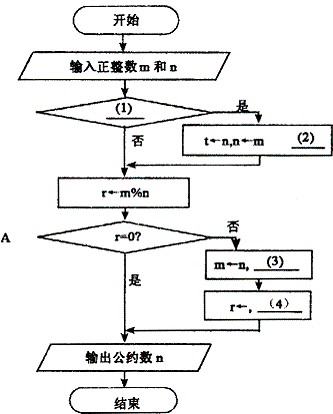
[问题1] 将流程图中的(1)~(4)处补充完整。
[问题2] 若输入的m和n分别为27和21,则A中循环体被执行的次数是(5)。
正确答案:[问题1] (1) n>m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1
[问题1] (1) n>m或nm或其它等效形式 (2) m←t (3) n←r (4) m%n [问题2] (5) 1 解析:(1)~(2)当n的值大于(等于)m时,应交换两者的值,再使用欧几里得算法;
(3)~(4)略;
(5)m,n和r在执行循环A前后的值分别为: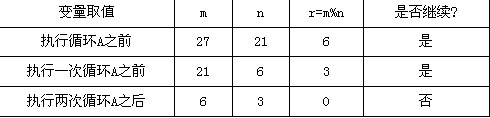
-
第2题:
请补充main函数,该函数的功能是:输入两个正整数numl和num2,求这两个数的最大公约和最小公倍数。
例如,若输入的两个正整数为12,4,则它们的最大公约数为12,最小公倍数为4。
注意:部分源程序给出如下。
请勿改动main函数和其他函数中的任何内容,仅在main函数的横线上填人所编写的若干表达式或语句。
试题程序:
include<stdlib.h>
include<stdio.h>
void main
{
int a,b,numl,num2,t;
system("CLS"):
printf("\nInput two numbers:\n");
scanf("%d,%d",&numl,&num2);
if(numl<num2)
{
a=num2;
b=num1:
}
else
{
a=num1;
b=num2;
}
while(【1】)
{
t=【2】
a=b;
b=t:
}
printf(“greatest common divisor:
%d\n",a);
printf("least common multiple:
%d\n",【3】;
}
正确答案:【1】b!=0【2】a%b[3]numl*num2/a
【解析】由程序可知,变量b中存放两个正整数中较小的那个数,while循环求两个正整数的公约数。因此【1】填“b!=0”;【2】填“a%b”.【3】处是求两个正整数最小公倍数的表达式,因此【3】填“numl*num2/a”。
-
第3题:
设{an}为数列,对于“存在正数肘,对任意正整数n,有 的否定(即数列{an}无界)是( )。
A、存在正数M,存在正整数n,使得|an|>M
的否定(即数列{an}无界)是( )。
A、存在正数M,存在正整数n,使得|an|>M
B、对任意正数M,存在正整数n,使得|an|>M
C、存在正数M,对任意正整数n,有|an|>M
D、对任意正数M以及任意正整数n,有|an|>M答案:B解析:对任意正数M,存在正整数n,使得
 则称数列{an}无界.
则称数列{an}无界. -
第4题:
求两个n阶矩阵的乘积,算法的基本操作和时间复杂度分别为()和()
乘法;O(n3)
略 -
第5题:
利用穷举法编写一个算法判断给定的正整数n是否是素数的程序,即判断n是否只能被1和自身整除。
正确答案: main( )
{
int m,i,k;
scanf("%d",&m);
k=sqrt(m);
for(i=2;i<=k;i++)
if(m%i==0) break;
if(i>=k+1)
printf("%d is a prime number/n",m);
else
printf("%d is not a prime number/n",m);
} -
第6题:
RSA算法计算实例(给定p,q,e,m/c,计算n,)(n,d,c/m)
正确答案: 1.选择素数:p=17&q=11
2.计算n=pq=17×11=187
3.计算ø(n)=(p–1)(q-1)=16×10=160
4.选择e:gcd(e,160)=1;选择e=7
5.确定d:de=1mod160andd<160,d=23因为23×7=161=1×160+1
6.公钥KU={7,187}
7.私钥KR={23,17,11} -
第7题:
奕泽发动机的最大功率和扭矩是?()
- A、115kw和198N.m
- B、126kw和198N.m
- C、115kw和203N.m
- D、126kw和203N.m
正确答案:D -
第8题:
子过程pfh(m,n)的功能是求两个数的平方和,现有已经赋值的变量a和b,求a和b的平方和的正确过程调用为()。
- A、Call pfh(a,b)
- B、pfh a,b
- C、pfh “a,b”
- D、pfh(a,b)
正确答案:A,B -
第9题:
对于整数环,任意两个非0整数a,b一定具有最大公因数可以用什么方法求?()
- A、分解法
- B、辗转相除法
- C、十字相乘法
- D、列项相消法
正确答案:B -
第10题:
问答题利用穷举法编写一个算法判断给定的正整数n是否是素数的程序,即判断n是否只能被1和自身整除。正确答案: main( )
{
int m,i,k;
scanf("%d",&m);
k=sqrt(m);
for(i=2;i<=k;i++)
if(m%i==0) break;
if(i>=k+1)
printf("%d is a prime number/n",m);
else
printf("%d is not a prime number/n",m);
}解析: 暂无解析 -
第11题:
问答题利用穷举法编写一个算法判断给定的正整数n是否是素数,即判断n是否只能被1和自身整除。正确答案: #include“math.h”
#include“stdio.h”
void main()
{
int m,i,k;
scanf("%d",&m);
ksqrt(m);
for(i=2;i<=k;i++)
if(m%i==0)break;
if(i>=k+1)
printf("%d is a prime number/n",m);
else
printf("%d is not a prime number/n",m);
}解析: 暂无解析 -
第12题:
单选题算法可以有0~n(设n、m为正整数)个输入,有()个输出。A0~m
B0
C1~m
D1
正确答案: A解析: 暂无解析 -
第13题:
请补充main函数,该函数的功能是:输入两个正整数m和n,求这两个数的最大公约和最小公倍数。
注意:部分源程序给出如下。
请勿改动主函数main和其他函数中的任何内容,仅在 main函数的横线上填入所编写的若干表达式或语句。
试题程序:
include <stdio.h>
main ( )
{
int a, b, n, m, t;
clrscr ();
printf ("\nInput two numbers: \n");
scanf ("%d, %d", &n, &m);
if (n<m)
{
a=m;
b=n;
}
else
{
a=n;
b=m;
}
while(【 】)
{
t=【 】
a=b;
b=t;
}
printf ("greatest con. non divisor:
%d\n", a);
printf ("least common multiple:
%d\n",【 】);
}
正确答案:b!=0 a%b; n*m/a
b!=0 a%b; n*m/a 解析:第一空:本题考查求最大公约数和最小公倍数的方法。变量a保存两数中较大着,变量b保存较小者,采用循环的方法求解最大公约数,循环结束条件是b等于0。第二空:求解最大公约数的思路是,将a对b求余,如果余数为0, 则b即为两数的最大公约数,如果余数不为0,则将b赋给a,余数赋给b,继续将a对b求余,如此循环,直到余数为0。第三空:最小公倍数等于两数的乘积除以最大公倍数。 -
第14题:
给定两个正整数m=630和n=675.利用辗转相除算法,求它们的最小公倍数。答案:解析:两个整数的最小公倍数=两整数的乘积÷最大公约数
求最大公约数的辗转相除法算法:
有两整数m和n:
①n%m得余数c;
②若c=0,则m即为两数的最大公约数;
③若c≠0,则n=m,m=c,再回去执行①。
求630和675的最大公约数过程为:
①675÷630.余45:
②630÷45余0,因此,45即为最大公约数。
最小公倍数=两整数的乘积÷最大公约数
即:最小公倍数=630×675÷45=9450。 -
第15题:
给定包含n个正整数的数组A和正整数x,要判断数组A中是否存在两个元素之和等于x,先用插入排序算法对数组A进行排序,再用以下过程P来判断是否存在两个元素之和等于x。low=1;high=n;while(high>low)if A[low]+A[high]=x return true;else if A[low]+A[high]>x low++;else high--;return false;则过程P的时间复杂度为( ),整个算法的时间复杂度为(请作答此空)。A.O(n)
B.O(nlgn)
C.O(n2)
D.O(n2lgn)答案:C解析:本题考查时间复杂度的基本知识。第一空有一层循环while,遍历判断,所以时间复杂度为n;第二空如图所示:插入排序的时间复杂为O(n2) ;故第一空正确答案为A;第二空正确答案为C;
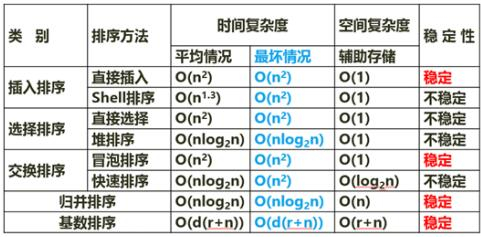
-
第16题:
采用辗转相除法求出两个整数的最大公约数。

a=b;b~r
略 -
第17题:
利用穷举法编写一个算法判断给定的正整数n是否是素数,即判断n是否只能被1和自身整除。
正确答案: #include“math.h”
#include“stdio.h”
void main()
{
int m,i,k;
scanf("%d",&m);
ksqrt(m);
for(i=2;i<=k;i++)
if(m%i==0)break;
if(i>=k+1)
printf("%d is a prime number/n",m);
else
printf("%d is not a prime number/n",m);
} -
第18题:
“中国剩余定理”即()的方法。
- A、大衍求一术
- B、辗转相除法
- C、四元术
- D、更相减损术
正确答案:A -
第19题:
两个整数的最小公倍数的求解一般以先求出它们的最大公约数,计算方法是两数相乘除以最大公约数。
正确答案:正确 -
第20题:
算法可以有0~n(设n、m为正整数)个输入,有()个输出。
- A、0~m
- B、0
- C、1~m
- D、1
正确答案:C -
第21题:
问答题RSA算法计算实例(给定p,q,e,m/c,计算n,)(n,d,c/m)正确答案: 1.选择素数:p=17&q=11
2.计算n=pq=17×11=187
3.计算ø(n)=(p–1)(q-1)=16×10=160
4.选择e:gcd(e,160)=1;选择e=7
5.确定d:de=1mod160andd<160,d=23因为23×7=161=1×160+1
6.公钥KU={7,187}
7.私钥KR={23,17,11}解析: 暂无解析 -
第22题:
单选题“中国剩余定理”即()的方法。A大衍求一术
B辗转相除法
C四元术
D更相减损术
正确答案: A解析: 暂无解析 -
第23题:
单选题对于整数环,任意两个非0整数a,b一定具有最大公因数可以用什么方法求?()A分解法
B辗转相除法
C十字相乘法
D列项相消法
正确答案: C解析: 暂无解析

