一质点沿半径R=1．6m的圆周运动，t=0时刻质点的位置为θ=0，质点的角速度w0=3．14s-1．若质点角加速度a=1．24t s-2。求：t=2．00 s时质点的速率、切向加速度和法向加速度。

题目
一质点沿半径R=1．6m的圆周运动，t=0时刻质点的位置为θ=0，质点的角速度w0=3．14s-1．若质点角加速度a=1．24t s-2。求：t=2．00 s时质点的速率、切向加速度和法向加速度。

相似考题

1.质点从t=0时刻开始由静止沿x轴运动，其加速度a=2ti(SI)，则当t=2s时该质点的速度大小为________m／s.

2.质点按照s=bt－1／2ct2的规律沿半径为R的圆周运动, 其中s是质点运动的路程,b、C是大于零的常量,并且b2>cR。问当切向加速度与法向加速度大小相等时,质点运动了多少时间?

3.质点沿半径为R=5m的圆周运动,其所行路程S与时间T的函数关系式为S=0.5T2＋3T(m),则2S内质点通过的路程和位移的大小为()A、6m;8.2mB、7m;6.5mC、6.5m;7mD、8m;7.2m

4.质点沿任意曲线运动,t时刻质点的极坐标为p(t)=beac,θ(t)=ct,试求此时刻质点的速度、加速度,并写出质点运动的轨道方程,式中α、b和c都是常量。

更多“一质点沿半径R=1．6m的圆周运动，t=0时刻质点的位置为θ=0，质点的角速度w0=3．14s-1．若质点角加速度a=1．24t s-2。求：t=2．00 s时质点的速率、切向加速度和法向加速度。”相关问题

  • 第1题：

    一质点沿直线运动，其运动方程为x=2+4t-2t2(SI)，在t从0到3s的时间间隔内，质点的位移大小为（ ）

    A．10m

    B．8m

    C．6m

    D．4m


    正确答案：C

  • 第2题：

    一质点作直线运动，已知其加速度a=2-2t，初始条件为xo=0，υo=0。
    (1)质点在第1秒末的速度；
    (2)质点的运动方程；
    (3)质点在前3秒内运动的路程。


    答案：
    解析：
    (1)求质点在任意时刻的速度


  • 第3题：

    一质点沿x轴正方向运动，的规律变化，式中k是正常数。当t=0时，质点位于原点0处。求该质点的速度及加速度随时间t的变化规律。


    答案：
    解析：

  • 第4题：

    一质点从静止出发，绕半径为R的圆周做匀变速圆周运动，角加速度为β，当该质点走完一周回到出发点时，所经历的时间（）



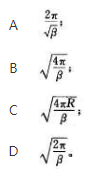    答案：B
    解析：

  • 第5题：

    两个质量相同的质点，沿相同的圆周运动，其中受力较大的质点（）。

    • A、切向加速度一定较大
    • B、法向加速度一定较大
    • C、不能确定加速度是否较大
    • D、全加速度一定较大

    正确答案:D

  • 第6题：

    一质点沿半径为R的圆周运动，在t=0时经过P点，此后它的速率v按v=A+Bt（A，B为正的已知常量）变化，则质点沿圆周运动一周再经过P点时的切向加速度at=（），法向加速度（）。


    正确答案:B；an=（A2/R）+4πB

  • 第7题：

    一质点P沿半径R的圆周作匀速率运动，运动一周所用时间为T，则质点切向加速度的大小为（）；法向加速度的大小为（）


    正确答案:0；4π2R/T2

  • 第8题：

    一质点沿x方向运动，其加速度随时间变化关系为a=3+2t，（SI）如果初始时质点的速度v0为5m/s，则当t为3s时，质点的速度v=（）。


    正确答案:23m/s

  • 第9题：

    一质点沿x轴作简谐振动，振动方程为x=0.04cos[2πt+（1/3）π]（SI），从t=0时刻起，到质点位置在x=-0.02m处，且向x轴正方向运动的最短时间间隔为（）

    • A、（1/8）s
    • B、（1/6）s
    • C、（1/4）s
    • D、（1/2）s

    正确答案:D

  • 第10题：

    一个质点在做匀速率圆周运动时，其切向加速度、法向加速度是否变化？


    正确答案:切向加速度不变，法向加速度变化

  • 第11题：

    质点沿x方向运动，其加速度随时间的变化关系为a=3+2t（SI），如果初始时刻质点的速度v0为5m·s-1，则当t为3s时，质点的速度v=（）。


    正确答案:23m·s-1

  • 第12题：

    填空题
    一质点作半径为R的匀速圆周运动，在此过程中质点的切向加速度的方向改（），法向加速度的大小（）。

    正确答案： 变,不变
    解析： 暂无解析

  • 第13题：

    已知质点沿半径为40cm的圆周运动，其运动规律为s=20t（s以cm计，t以s计）。若t=1s，则点的速度与加速度的大小为：


    答案：B
    解析：

  • 第14题：

    一列简谐横波沿x轴传播，t=0时刻的波形如图4所示，则从图中可以看出()。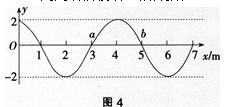



    A.这列波的波长为5m

    B.波中的每个质点的振动周期为4S

    C.若已知波沿x轴正向传播．则此时质点a向下振动

    D.若已知质点b此时向上振动，则波是沿x轴负向传播的

    答案：C
    解析：

  • 第15题：

    质点作匀速圆周运动时，既有法向加速度，又有切向加速度。()


    答案：对
    解析：

  • 第16题：

    一质点沿y轴方向做简谐振动，振幅为A，周期为T，平衡位置在坐标原点。在t=0时刻，质点位于y正向最大位移处，以此振动质点为波源，传播的横波波长为λ，则沿x轴正方向传播的横波方程为（ ）。



    答案：C
    解析：

  • 第17题：

    质量为10kg的质点，受水平力F的作用在光滑水平面上运动，设 F=2+6t（t以s计， F以 N计），初瞬时（t=0）质点位于坐标原点。且初速度为零。则当t=2s时，质点的位移和速度分别为（）。

    • A、1.2m和1.6m/s
    • B、1.4m和1.6m/s
    • C、1.6m和1.2m/s
    • D、2m和1.6m/s

    正确答案:A

  • 第18题：

    一质点沿x轴运动V=1+3t2（m/s）。若t=0时，质点位于原点，则t=2s时，质点加速度的大小a=（），质点的坐标X=（）。


    正确答案:12m/s-1；10m

  • 第19题：

    一质点沿x方向运动，其加速度随时间变化关系为：a=3+2t，如果初始时刻质点的速度v0为5m/s，则当ｔ为3s时，质点的速度（）


    正确答案:v=23m/s

  • 第20题：

    一质点沿半径为0.2m的圆周运动，其角位置随时间的变化规律是θ=6+5t2（SI制）。在t=2s时，它的法向加速度an=（）；切向加速度aτ=（）。


    正确答案:80rad/s2；2rad/s2

  • 第21题：

    一质点从静止出发沿半径R=1m的圆周运动，其角加速度随时间t的变化规律是（），则质点的角速度（）


    正确答案:12t2-6t；4t3-3t2 (rad/s)

  • 第22题：

    一质点，以πm·s-1的匀速率作半径为5m的圆周运动，则该质点在5s内，位移的大小是（）；经过的路程是（）。


    正确答案:10m；5πm

  • 第23题：

    质点作曲线运动，在时刻t质点的位矢为r，速度为v，速率为v，t 至（t ＋Δt）时间内的位移为Δr，路程为Δs，位矢大小的变化量为Δr（或称Δ｜r｜），平均速度为v，平均速率为v。根据上述情况，则必有（）

    • A、｜Δr｜=Δs=Δr
    • B、｜Δr｜≠Δs≠Δr，当Δt→0时有｜dr｜=ds≠dr
    • C、｜Δr｜≠Δr≠Δs，当Δt→0时有｜dr｜=dr≠ds
    • D、｜Δr｜≠Δs≠Δr，当Δt→0时有｜dr｜=dr=ds

    正确答案:B

相关内容