《代入法解二元一次方程组》 一、面试考题 试讲题目 1.题目：代入法解二元一次方程组 2.内容：3.基本要求： (1)试讲时间10分钟以内; (2)讲解要目的明确、条理清楚、重点突出; (3)根据讲解的需要适当板书; (4)结合例子归纳代入法解二元一次方程组的思路及步骤。 答辩题目 1.二元一次方程组有哪些解法? 2.你是如何引导学生掌握二元一次方程组的解法的? 注：图片节选自北京师范大学出版社初中数学八年级上册第109页

题目
《代入法解二元一次方程组》
一、面试考题
试讲题目
1.题目：代入法解二元一次方程组
2.内容：

3.基本要求：
(1)试讲时间10分钟以内;
(2)讲解要目的明确、条理清楚、重点突出;
(3)根据讲解的需要适当板书;
(4)结合例子归纳代入法解二元一次方程组的思路及步骤。
答辩题目
1.二元一次方程组有哪些解法?
2.你是如何引导学生掌握二元一次方程组的解法的?
注：图片节选自北京师范大学出版社初中数学八年级上册第109页

相似考题

1.设线性方程组AX=b有唯一解,则相应的齐次方程组AX=0解的情况是()。A.有非零解B.只有零解C.无解D.解不能确定

2.牛顿－拉夫逊迭代法的基本原理是用泰勒级数展开非线性方程组,略去二阶及以上的高阶项得到线性修正方程组,通过一次求解修正方程组和修正未知量就可得到未知量的精确解。()此题为判断题(对，错)。

3.用列主元消去法解线性方程组,A、3B、4C、-4D、9

4.非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()

更多“《代入法解二元一次方程组》 ”相关问题

  • 第1题：

    回顾本书第六章第5节的有关例题、习题，你能通过二元一次方程组来获得问题的解答吗？


    例如已知一次函数经过的两点，求一次函数表达式的问题，其实质就是解二元一次方程组的问题！！

  • 第2题：

    我二元一次方程组x+y=9 2x-y=3的解为

    A.x=7y=2

    B.x=4y=5

    C.x=3y=6

    D.x=2y=7


    正确答案：B

  • 第3题：

    已知是线性方程组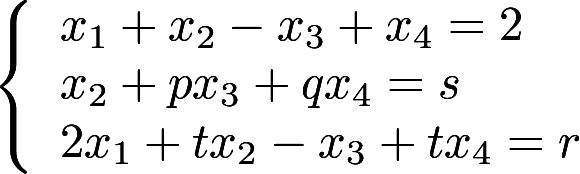的解, 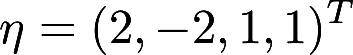是它的导出组的解,求方程组的通解。


    答案：
    解析：

  • 第4题：

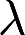    取何值时,非齐次线性方程组 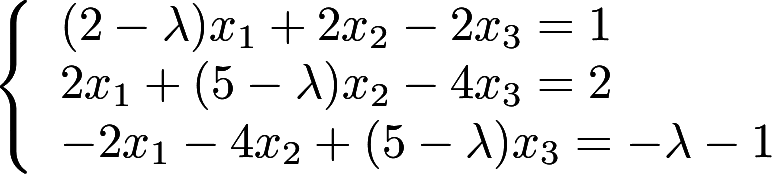(1)有唯一解 (2)无解 (3)有无穷多个解? 并在无穷多个解时，求方程组的通解。


    答案：
    解析：

  • 第5题：

    已知方程组(I)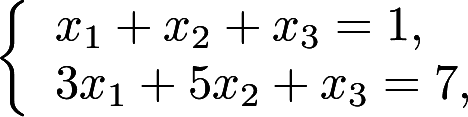(II)图1} (1)a,b取什么值时这两个方程组同解?此时求解. (2)a,b取什么值时这两个方程组有公共解? 此时求公共解{


    答案：
    解析：

  • 第6题：

    采用对流换热边界层微分方程组、积分方程组或雷诺类比法求解，对流换热过程中，正确的说法是（　　）。

    A． 微分方程组的解是精确解
    B． 积分方程组的解是精确解
    C． 雷诺类比的解是精确解
    D． 以上三种均为近似解

    答案：A
    解析：
    对流换热的求解方法包括分析法、类比法和实验法。分析法包括微分方程组求解和积分方程组求解。在所有方法中，只有微分方程组的解是精确解；积分方程组的求解要先假设速度和温度的分布，因此是近似解；雷诺类比的解是由比拟理论求得的，也是近似解。

  • 第7题：

    设线性方程组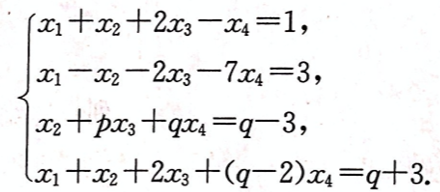问方程组何时无解，有唯一解，有无穷多解，有无穷多解时，求出其全部解。


    答案：
    解析：
    将方程组的增广矩阵作初等行变换，有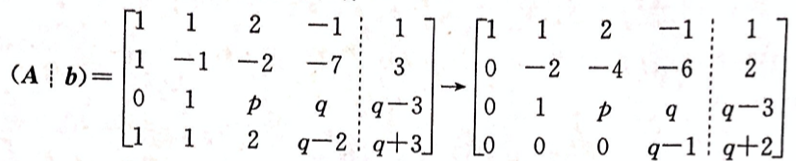

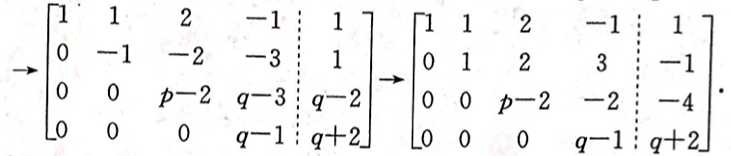
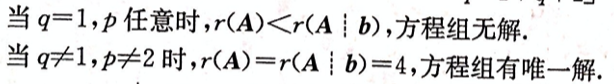
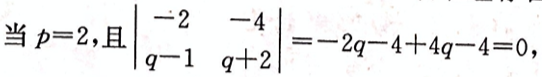
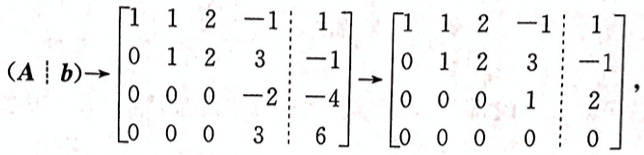
  • 第8题：

    初中数学《解二元一次方程组》
    一、考题回顾
    题目来源:5月18日 上午 湖北省黄石市 面试考题
    试讲题目
    1.题目：解二元一次方程组
    2.内容：



    3.基本要求：
    (1)要有板书，试讲十分钟左右;
    (2)条理清晰，重点突出;
    (3)学生掌握解二元一次方程组的基本方法。
    答辩题目
    1.本节课采用了什么教学方法?
    2.二元一次方程组有哪些解法?


    答案：
    解析：
    二、考题解析
    【教学过程】
    (一)导入新课
    多媒体展示：篮球比赛规则规定：赢一场得2分，输一场得1分，在中学生篮球联赛中，某球队赛了12场，共得20分，则该球队赢了几场?输了几场?
    提问：对于这样有两个未知数的一道题，我们可以如何列式解决呢?





    【答辩题目解析】
    1.本节课采用了什么教学方法?
    【参考答案】
    数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础上。学生是数学学习的主人，教师是数学学习的组织者、引导者和合作者。
    所以在这节课中我采用了小组讨论法和讲解法、练习法相结合的教学方法。让学生带着问题学、在探索中学、在合作交流中学。在教学中积极培养学生的学习兴趣和动机，明确学习目的。
    2.解二元一次方程组的解法有哪些?
    【参考答案】
    加减消元，代入消元。

  • 第9题：

    将鸡兔同笼问题，转化为求解二元一次方程组的问题，这就是建立数学模型。（）


    正确答案:正确

  • 第10题：

    紫外－可见分光光度法中多组分定量方法中，如果两组分吸收曲线重叠时候可以采用（）定量。

    • A、解二元一次联立方程组
    • B、解二元二次联立方程组
    • C、解一元二次联立方程组
    • D、解二元三次联立方程组

    正确答案:A

  • 第11题：

    问答题
    设AX=0与BX=0均为n元齐次线性方程组，秩r（A）=r（B），且方程组AX=0的解均为方程组BX=0的解，证明方程组AX=0与BX=0同解.

    正确答案：
    设r(A)=r(B)=r,方程组AX=0的基础解系为①:ζ1,ζ2,…,ζn-r,方程组BX=0的基础解系为②:η1,η2,…,ηn-r.
    构造向量组③:ζ1,ζ2,…,ζn-r,η1,η2,…,ηn-r.
    由向量组①可由②线性表示,则向量组②和③等价,从而r(③)=n-r,所以ζ1,ζ2,…,ζn-r是向量组③的极大线性无关组,有η1,η2,…,ηn-r可由ζ1,ζ2,…,ζn-r线性表示,即BX=0的任一解都可由ζ1,ζ2,…,ζn-r线性表示,故BX=0的解都是AX=0的解,所以方程组AX=0与BX=0同解.
    解析： 暂无解析

  • 第12题：

    单选题
    采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（  ）。
    A

    微分方程组的解是精确解

    B

    积分方程组的解是精确解

    C

    雷诺类比的解是精确解

    D

    以上三种均为近似值


    正确答案： D
    解析：

  • 第13题：

    我国古代数字著作《孙子算法》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有九十四足。问鸡兔各几何。”你能用二元一次方程组表示题中的数量关系吗？试找出问题的解。

  • 第14题：

    设A是m×n阶矩阵,下列命题正确的是().

    A.若方程组AX=0只有零解,则方程组AX=b有唯一解
    B.若方程组AX=0有非零解,则方程组AX=b有无穷多个解
    C.若方程组AX=b无解,则方程组AX=0一定有非零解
    D.若方程组AX=b有无穷多个解,则方程组AX=0一定有非零解

    答案：D
    解析：

  • 第15题：

    讨论方程组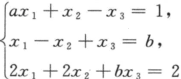的解的情况,在方程组有解时求出其解,其中a,b为常数.


    答案：
    解析：

  • 第16题：

    设齐次线性方程组
    　　
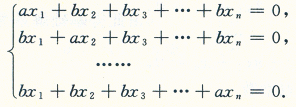
    　　其中a≠0，b≠0，n≥2.试讨论a，b为何值时，方程组仅有零解，有无穷多组解？在有无穷多组解时，求出全部解，并用基础解系表示全部解.


    答案：
    解析：

  • 第17题：

    已知下列非齐次线性方程组(Ⅰ)，(Ⅱ)
    　　
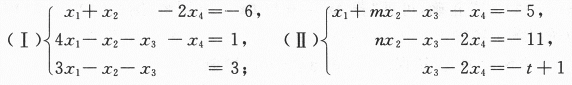
    　　(1)求解方程组(Ⅰ)，用其导出组的基础解系表示通解.
    　　(2)当方程组中的参数m，n，t为何值时，方程组(Ⅰ)与(Ⅱ)同解.


    答案：
    解析：

  • 第18题：

    已知齐次线性方程组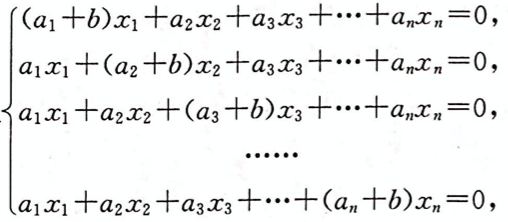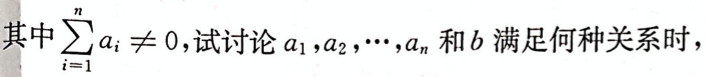（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.


    答案：
    解析：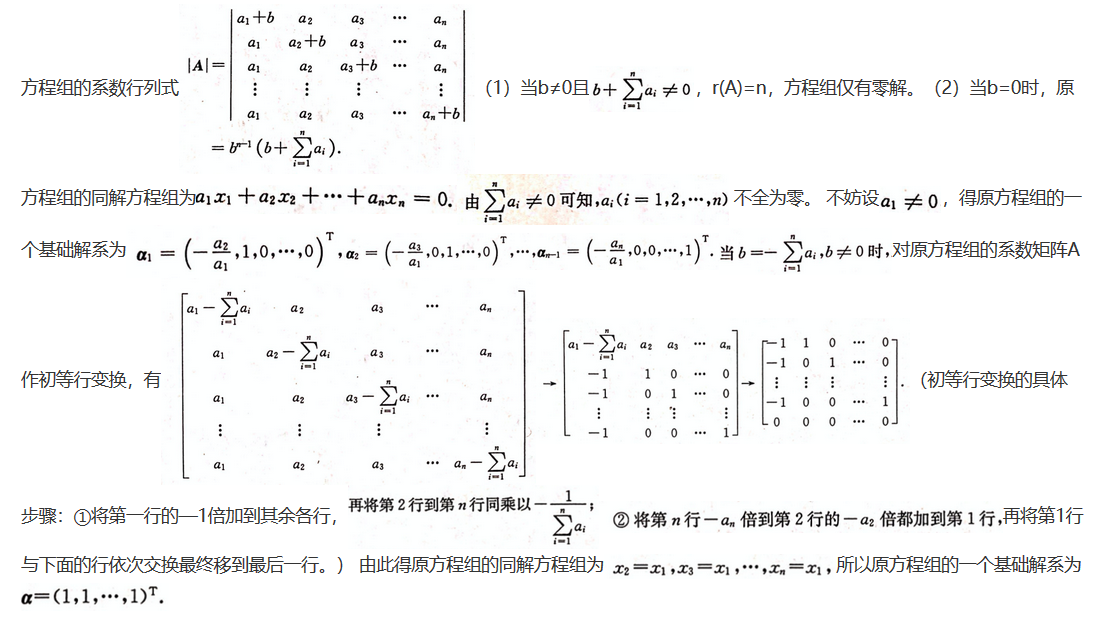

  • 第19题：

    一、考题回顾
    题目来源：1月6日上午陕西省西安市面试考题
    试讲题目：初中数学《实际问题与二元一次方程组》

    基本要求:
    (1) 要有板书;
    (2 )试讲十分钟左右;
    (3) 条理清晰，重点突出;
    (4) 学生掌握利用二元一次方程组解决实际问题的方法。
    答辩题目
    1.在本节课的课堂教学中，涉及到了什么数学思想?
    2 如何引导学生熟练地解二元一次方程组?


    答案：
    解析：

  • 第20题：

    解线性方程组Ax=b的高斯顺序消元法满足的充要条件为（）。


    正确答案:A的各阶顺序主子式均不为零

  • 第21题：

    应用哈代—克罗斯法解环方程组的步骤怎样？


    正确答案: 应用哈代—克罗斯法解环方程组的步骤：
    1）根据城镇的供水情况，拟定环状网各管段的水流方向，得出初步分配流量；
    2）由初分流量计算各管段的摩阻系数和水头损失；
    3）假定各环水流顺时针方向管段中的水头损失为正，逆时针方向管段中的水头损失为负，计算该环内各管段的水头损失代数和，如果代数和大于零，说明顺时针方向各管段中初分流量多了些，逆时针方向各管段中初分流量少了些，如果代数和小于零，说明逆时针方向各管段中初分流量多了些，顺时针方向各管段中初分流量少了些；
    4）求出校正流量，如果闭和差为正，校正流量即为负，反之校正流量为正；
    5）利用校正流量调整各管段的流量，得到第一次校正的管段流量，按此流量再进行计算，如果闭和差尚未达到允许的精度，返回到第2步再进行计算，直到闭和差符合要求为止。

  • 第22题：

    单选题
    采用对流换热边界层微分方程组，积分方程组或雷诺类比法求解对流换热过程中，正确的说法是（　　）。[2010年真题]
    A

    微分方程组的解是精确解

    B

    积分方程组的解是精确解

    C

    雷诺类比的解是精确解

    D

    以上三种均为近似值


    正确答案： A
    解析：
    对流换热的求解方法包括分析法、类比法和实验法。分析法包括微分方程组求解和积分方程组求解。在所有方法中，只有微分方程组的解是精确解；积分方程组的求解要先假设速度和温度的分布，因此是近似解；雷诺类比的解是由比拟理论求得的，也是近似解。

  • 第23题：

    问答题
    应用哈代—克罗斯法解环方程组的步骤怎样？

    正确答案： 应用哈代—克罗斯法解环方程组的步骤：
    1）根据城镇的供水情况，拟定环状网各管段的水流方向，得出初步分配流量；
    2）由初分流量计算各管段的摩阻系数和水头损失；
    3）假定各环水流顺时针方向管段中的水头损失为正，逆时针方向管段中的水头损失为负，计算该环内各管段的水头损失代数和，如果代数和大于零，说明顺时针方向各管段中初分流量多了些，逆时针方向各管段中初分流量少了些，如果代数和小于零，说明逆时针方向各管段中初分流量多了些，顺时针方向各管段中初分流量少了些；
    4）求出校正流量，如果闭和差为正，校正流量即为负，反之校正流量为正；
    5）利用校正流量调整各管段的流量，得到第一次校正的管段流量，按此流量再进行计算，如果闭和差尚未达到允许的精度，返回到第2步再进行计算，直到闭和差符合要求为止。
    解析： 暂无解析

相关内容