4、关于背包问题,正确的是()A.01背包用动态规划求解,部分背包用贪心算法求解B.01背包用贪心算法求解,部分背包用动态规划求解C.背包问题都用贪心算法求解D.背包问题都用动态规划求解
题目
4、关于背包问题,正确的是()
A.01背包用动态规划求解,部分背包用贪心算法求解
B.01背包用贪心算法求解,部分背包用动态规划求解
C.背包问题都用贪心算法求解
D.背包问题都用动态规划求解
相似考题
更多“4、关于背包问题,正确的是()”相关问题
-
第1题:
*部分背包问题可有贪心法求解:计算Pi/Wi
数据结构:
w[i]:第i个背包的重量;
p[i]:第i个背包的价值;
1.0-1背包: 每个背包只能使用一次或有限次(可转化为一次):
A.求最多可放入的重量。
正确答案:NOIP2001 装箱问题
有一个箱子容量为v(正整数,o≤v≤20000),同时有n个物品(o≤n≤30),每个物品有一个体积 (正整数)。要求从 n 个物品中,任取若千个装入箱内,使箱子的剩余空间为最小。
l 搜索方法
procedure search(k,v:integer); {搜索第k个物品,剩余空间为v}
var i,j:integer;
begin
if v<best then best:=v;
if v-(s[n]-s[k-1])>=best then exit; {s[n]为前n个物品的重量和}
if k<=n then begin
if v>w[k] then search(k+1,v-w[k]);
search(k+1,v);
end;
end;l DP
F[I,j]为前i个物品中选择若干个放入使其体积正好为j的标志,为布尔型。
实现:将最优化问题转化为判定性问题
f [I, j] = f [ i-1, j-w[i] ] (w[I]<=j<=v) 边界:f[0,0]:=true.
For I:=1 to n do
For j:=w[I] to v do F[I,j]:=f[I-1,j-w[I]];
优化:当前状态只与前一阶段状态有关,可降至一维。
F[0]:=true;
For I:=1 to n do begin
F1:=f;
For j:=w[I] to v do
If f[j-w[I]] then f1[j]:=true;
F:=f1;
End; -
第2题:
关于RSA的描述中,错误的是
A)是一种分组密码算法
B)可用于数字签名
C)用发明者名字命名
D)基于背包问题
正确答案:D
【答案】D)
【解析】RSA是一个既能用于数据加密也能用于数字签名的算法。算法的名字以发明者的名字命名:ron rivest 、adi shamir和leonard adleman。RSA是一种分组密码。背包加密算法是以求解背包问题的计算困难性为基础的。 -
第3题:
考虑下述背包问题的实例。有5件物品,背包容量为100,每件物品的价值和重量如下表所示,并已经按照物品的单位重量价值从大到小徘好序,根据物品单位重量价值大优先的策略装入背包中,则采用了( )设计策略。考虑0/1背包问题(每件物品或者全部放入或者全部不装入背包)和部分背包问题(物品可以部分装入背包),求解该实例,得到的最大价值分别为(请作答此空)。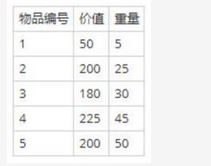 A.605和630
A.605和630
B.605和605
C.430和630
D.630和430答案:C解析:贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。0/1背包考虑该问题时,只能放入1、2、3号物品,故总价值为430,采用部分背包问题可以将物品拆分,故放1、2、3号物品后还可以放入部分4号物品,故总容量为630。 -
第4题:
采用贪心算法保证能求得最优解的问题是( )A.0-1背包
B.矩阵连乘
C.最长公共子序列
D.邻分(分数)背包答案:D解析:动态规划算法适合解决0-1背包问题,贪心法适合解决部分背包(邻分(分数)背包)问题。 -
第5题:
关于0-1背包问题以下描述正确的是()
- A、可以使用贪心算法找到最优解
- B、能找到多项式时间的有效算法
- C、使用教材介绍的动态规划方法可求解任意0-1背包问题
- D、对于同一背包与相同的物品,做背包问题取得的总价值一定大于等于做0-1背包问题
正确答案:D -
第6题:
简述运筹学中背包问题的一般提法。
正确答案: 对于N种具有不同重量和不同价值的物品,在携带物品总重量限制的情况下,决定这N种物品中每一种物品多少数量装入背包内,使得装入背包物品的总价值最大。 -
第7题:
有这样一类特殊0-1背包问题:可选物品重量越轻的物品价值越高。 n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大,能获得的最大总价值多少?
正确答案: 因为该0-1背包问题比较特殊,恰好重量越轻的物品价值越高,所以优先取重量轻的物品放进背包。最终可以把重量分别为2,3,4,5的三个物品放进背包,得到的价值和为15+8+6+4=33,为最大值。 -
第8题:
关于背包加密算法的描述中,正确的是()
- A、保证绝对安全
- B、物品总重量公开
- C、背包问题属于NP问题
- D、属于对称加密算法
- E、一次背包已不安全
正确答案:B,C,E -
第9题:
举反例证明0/1背包问题若使用的算法是按照pi/wi的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解(此题说明0/1背包问题与背包问题的不同)。
正确答案: 举例如:
p{7,4,4},w={3,2,2},c=4时,
由于7/3最大,
若按题目要求的方法,只能取第一个,收益是7。
而此实例的最大的收益应该是8,取第2,3 个。 -
第10题:
单选题关于0-1背包问题以下描述正确的是()A可以使用贪心算法找到最优解
B能找到多项式时间的有效算法
C使用教材介绍的动态规划方法可求解任意0-1背包问题
D对于同一背包与相同的物品,做背包问题取得的总价值一定大于等于做0-1背包问题
正确答案: B解析: 暂无解析 -
第11题:
问答题有这样一类特殊0-1背包问题:可选物品重量越轻的物品价值越高。 n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大,能获得的最大总价值多少?正确答案: 因为该0-1背包问题比较特殊,恰好重量越轻的物品价值越高,所以优先取重量轻的物品放进背包。最终可以把重量分别为2,3,4,5的三个物品放进背包,得到的价值和为15+8+6+4=33,为最大值。解析: 暂无解析 -
第12题:
单选题RSA体制的安全性是基于()。A大整数分解问题
B离散对数问题
C背包问题
D格困难问题
正确答案: C解析: 暂无解析 -
第13题:
考虑一个背包问题,共有n=5个物品,背包容量为W=10,物品的重量和价值分别为:w={2,2,6,5,4},v={6,3,5,4,6},求背包问题的最大装包价值。若此为0-1背包问题,分析该问题具有最优子结构,定义递归式为

其中c(i,j)表示i个物品、容量为j的0-1背包问题的最大装包价值,最终要求解c(n,W)。 采用自底向上的动态规划方法求解,得到最大装包价值为(62),算法的时间复杂度为(63)。 若此为部分背包问题,首先采用归并排序算法,根据物品的单位重量价值从大到小排序,然后依次将物品放入背包直至所有物品放入背包中或者背包再无容量,则得到的最大装包价值为(64),算法的时间复杂度为(65)。
A.11
B.14
C.15
D.16.67
正确答案:C
-
第14题:
考虑下述背包问题的实例。有5件物品,背包容量为100,每件物品的价值和重量如下表所示,并已经按照物品的单位重量价值从大到小徘好序,根据物品单位重量价值大优先的策略装入背包中,则采用了(请作答此空)设计策略。考虑0/1背包问题(每件物品或者全部放入或者全部不装入背包)和部分背包问题(物品可以部分装入背包),求解该实例,得到的最大价值分别为( )。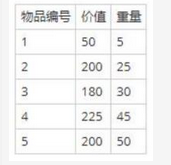 A.分治
A.分治
B.贪心
C.动态规划
D.回溯答案:B解析:贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。0/1背包考虑该问题时,只能放入1、2、3号物品,故总价值为430,采用部分背包问题可以将物品拆分,故放1、2、3号物品后还可以放入部分4号物品,故总容量为630。 -
第15题:
阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。【说明】0-1背包问题定义为:给定1个物品的价值v[1....i]、重量w[1....i]和背包容量T,每个物品装到背包里或者不装到背包里,求最优的装包方案,使得所得到的价值最大。0-1背创问题具有最优子结构性质,定义c为最优装包方案所获得的最大价值则可得到如下所示的递归式。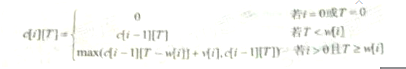
【C代码】下面是算法的C语言实现(1)常量和变量说明T:背包容量V[]:价值数组W[]:重量数组C[][]:c[i][j]表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值(2)C程序

【问题1】(8分)根据说明和C代码,填充C代码中的空(1)~(4)【问题2】(4分)根据说明和C代码,算法采用了(5)设计策略。在求解过程中,采用了(6)(自底向上或者自顶向下)的方式。【问题3】(3分)若5项物品的价值数组和重量数组分别为v[]={0,1,6,18,22,28}和w[]={0,1,2,5,6,7},背包容量为T=11,则获得的最大价值为(7)。答案:解析:问题1:1:c[i][j]2: temp第16题:
有0-1背包问题如下: n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大。 P=(15,8,6,4,3,1),W=(2,3,4,5,8,10),单位重量物品价值(7.5,2.67,1.5,0.8,0.375,0.1)
正确答案: 可知随着物品的重量增加,物品的价值减少;因此可以用贪心算法来求解。以选取单位重量物品价值高为贪心策略。
1.先把重量为2的物品放进背包,此时剩余载重量为17,P为15。
2.把重量为3的物品放进背包,此时剩余载重量为14,P为23;
3.把重量为4的物品放进背包,此时剩余载重量为10,P为29;
4.把重量为5的物品放进背包,此时剩余载重量为5,P为33;
由于8>5,所以不能再放进背包。
结果是把重量为2,3,4,5的物品装进背包,总价值最大为33。第17题:
对于0-1背包问题和背包问题的解法,下面()答案解释正确。
- A、0-1背包问题和背包问题都可用贪心算法求解
- B、0-1背包问题可用贪心算法求解,但背包问题则不能用贪心算法求解
- C、0-1背包问题不能用贪心算法求解,但可以使用动态规划或搜索算法求解,而背包问题则可以用贪心算法求解
- D、因为0-1背包问题不具有最优子结构性质,所以不能用贪心算法求解
正确答案:C第18题:
乘坐公交车时防止被盗,下列说法正确的是()
- A、背包放在身后
- B、时刻盯着背包看
- C、上下车抱在胸前
正确答案:C第19题:
在0-1背包问题中,若各物品依重量递增序排列时,其价值恰好依递减序排列,对这个特殊的0-1背包问题,设计一个有效的算法找出最优解。(描述你的算法即可,无需证明算法的正确性)
正确答案: 对于0-1背包问题本来是无法用贪心算法得到最优解的,但对于这类特殊的0-1背包问题,则可以用贪心算法去解。贪心策略如下:
首先将各物品依重量递增序(即也是价值递减序)排列,然后依照价值递减顺序选择物品装入背包,直到背包装不下下一件物品为止。
这里贪心算法的贪心选择策略是:每次总是选择价值最大(同时重量也最小)的物品,然后检查是否可以装入背包。第20题:
描述0-1背包问题。
正确答案:已知一个背包的容量为C,有n件物品,物品i的重量为Wi,价值为Vi,求应如何选择装入背包中的物品,使得装入背包中物品的总价值最大。第21题:
问答题举反例证明0/1背包问题若使用的算法是按照pi/wi的非递减次序考虑选择的物品,即只要正在被考虑的物品装得进就装入背包,则此方法不一定能得到最优解(此题说明0/1背包问题与背包问题的不同)。正确答案: 举例如:
p{7,4,4},w={3,2,2},c=4时,
由于7/3最大,
若按题目要求的方法,只能取第一个,收益是7。
而此实例的最大的收益应该是8,取第2,3 个。解析: 暂无解析第22题:
问答题有0-1背包问题如下: n=6,c=20,P=(4,8,15,1,6,3),W=(5,3,2,10,4,8)。 其中n为物品个数,c为背包载重量,P表示物品的价值,W表示物品的重量。请问对于此0-1背包问题,应如何选择放进去的物品,才能使到放进背包的物品总价值最大。 P=(15,8,6,4,3,1),W=(2,3,4,5,8,10),单位重量物品价值(7.5,2.67,1.5,0.8,0.375,0.1)正确答案: 可知随着物品的重量增加,物品的价值减少;因此可以用贪心算法来求解。以选取单位重量物品价值高为贪心策略。
1.先把重量为2的物品放进背包,此时剩余载重量为17,P为15。
2.把重量为3的物品放进背包,此时剩余载重量为14,P为23;
3.把重量为4的物品放进背包,此时剩余载重量为10,P为29;
4.把重量为5的物品放进背包,此时剩余载重量为5,P为33;
由于8>5,所以不能再放进背包。
结果是把重量为2,3,4,5的物品装进背包,总价值最大为33。解析: 暂无解析第23题:
问答题描述0-1背包问题。正确答案: 已知一个背包的容量为C,有n件物品,物品i的重量为Wi,价值为Vi,求应如何选择装入背包中的物品,使得装入背包中物品的总价值最大。解析: 暂无解析第24题:
问答题在0-1背包问题中,若各物品依重量递增序排列时,其价值恰好依递减序排列,对这个特殊的0-1背包问题,设计一个有效的算法找出最优解。(描述你的算法即可,无需证明算法的正确性)正确答案: 对于0-1背包问题本来是无法用贪心算法得到最优解的,但对于这类特殊的0-1背包问题,则可以用贪心算法去解。贪心策略如下:
首先将各物品依重量递增序(即也是价值递减序)排列,然后依照价值递减顺序选择物品装入背包,直到背包装不下下一件物品为止。
这里贪心算法的贪心选择策略是:每次总是选择价值最大(同时重量也最小)的物品,然后检查是否可以装入背包。解析: 暂无解析
