58、对于一个二维随机变量，如果这两个随机变量相互独立，则由它的两个边缘分布函数可以确定出它的联合分布函数.

题目

58、对于一个二维随机变量，如果这两个随机变量相互独立，则由它的两个边缘分布函数可以确定出它的联合分布函数.

相似考题

1.若两个随机变量的联合分布是二元正态分布,如果他们的相关系数为0则他们是相互独立的。()此题为判断题(对，错)。

2.随机变量X的分布函数F(X)是X的非减函数。()

3.随机变量的分布函数 名词解释

4.如果随机变量X的分布函数F(X)可以表示成一个非负可积函数f(x)的积分，则称X为连续型随机变量。()

参考答案和解析
正确
更多“58、对于一个二维随机变量，如果这两个随机变量相互独立，则由它的两个边缘分布函数可以确定出它的联合分布函数.”相关问题

  • 第1题：

    对于两个随机变量的联合分布,两个随机变量的相关系数为0则他们可能是相互独立的。()

    此题为判断题(对，错)。


    参考答案：错

  • 第2题：

    设随机变量X的分布函数


    答案：C
    解析：

  • 第3题：

    设随机变量X服从参数为1的指数分布,则随机变量y=min{X,2）的分布函数().



    A.是阶梯函数
    B.恰有一个间断点
    C.至少有两个间断点
    D.是连续函数

    答案：B
    解析：

  • 第4题：

    设二维随机变量(X,Y)的联合密度函数为f(x,y)=
    　　(1)求随机变量X,Y的边缘密度函数；
    　　(2)判断随机变量X,Y是否相互独立；
    　　(3)求随机变量Z=X+2Y的分布函数和密度函数.


    答案：
    解析：

  • 第5题：

    设离散型随机变量x的分布函数为

    则Y=X^2+1的分布函数为_______.


    答案：
    解析：
    X的分布律为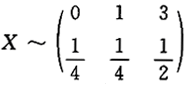，Y的可能取值为1，2，10，　　

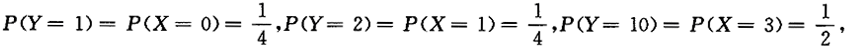
    于是Y的分布函数为
    　　

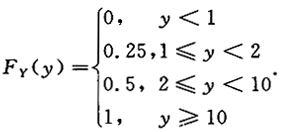
  • 第6题：

    设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3.
    　　设随机变量U=max{X,Y},V=min{X,Y}.
    　　(1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布；
    　　(3)判断U,V是否相互独立？(4)求P（U=V）.


    答案：
    解析：

  • 第7题：

    设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=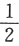.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为

    A.A0
    B.1
    C.2
    D.3

    答案：D
    解析：

  • 第8题：

    设随机变量X的分布函数为，其中为标准正态分布函数，则EX=________.


    答案：1、2.
    解析：

  • 第9题：

    已知 X1 和 X2 是相互独立的随机变量，分布函数分别为F1（x）和F2（x），则下列选项一定是某一随机变量分布函数的为（ ）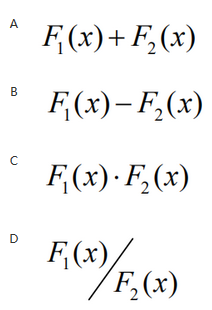


    答案：C
    解析：
    分布函数要满足非负性，规范性，单调不减性，右连续性.

  • 第10题：

    随机变量X的分布函数F（x）是一个实函数，其定义域是（）；值域是（）。


    正确答案:（-∞，+∞）；[0，1]

  • 第11题：

    随机变量的X分布函数F（X）是右连续函数。


    正确答案:正确

  • 第12题：

    单选题
    下列选项中正确的是（）。
    A

    两个泊松分布之差还是泊松分布

    B

    若两个二维分布有相同的边缘分布，则它们一定相同

    C

    若X为随机变量且X2服从χ2分布，则X服从正态分布

    D

    任意两个分布函数之和一定还是分布函数

    E

    以上选项都不正确


    正确答案： D
    解析： 暂无解析

  • 第13题：

    下列函数中，可以作为连续型随机变量的分布函数的是：


    答案：B
    解析：
    提示：分布函数[记为Q（x）]性质：（1）0≤Q（x）≤1，Q（-∞）=0，Q（+∞）=1；（2）Q（x）是非减函数；（3）Q（x）是右连续的。
    Φ（+∞）=-∞；F（x）满足分布函数的性质（1）、（2）、（3）；
    G（-∞）= +∞，x≥0时，H（x）>1。

  • 第14题：

    设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().



    A.F(z)=F（-x）
    B.F(x)=F（-x）
    C.F(X)=F（-x）
    D.f(x)=f（-x）

    答案：C
    解析：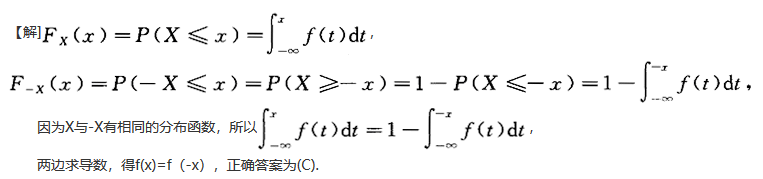

  • 第15题：

    设随机变量X,Y相互独立,它们的分布函数为Fx(x),F(y),则Z=min{X,Y}的分布函数为().


    答案：C
    解析：
    FZ(z)=P(Z≤z)=P(min{X,Y}≤z)=1-P(min{X,Y}>z)　　=1-P(X>z,Y>z)=1-P(X>z)P(Y>z)
    　　=1-【1-P(X≤z)】【1-P(Y≤z)】=1-【1-FX(z)】【1-FY(z)】，选(C).

  • 第16题：

    设随机变量X与Y相互独立,下表列出二维随机变量(X,Y)的联合分布律及关于X和Y的边缘分布律的部分数值,试将其余的数值填入表中空白处.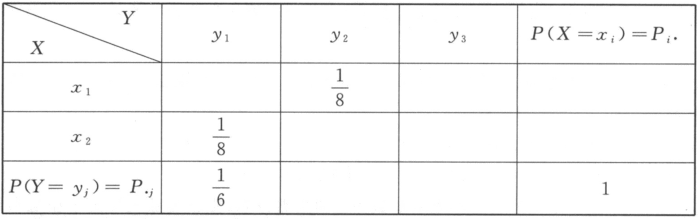


    答案：
    解析：

  • 第17题：

    设随机变量X和Y相互独立,且分布函数为Fx(x)=,Fy(y)=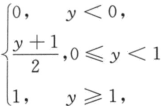,令U=X+Y,则U的分布函数为_______.


    答案：
    解析：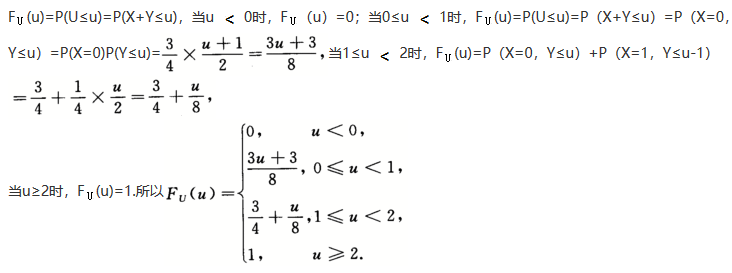

  • 第18题：

    设随机变量X和Y相互独立，下表列出了二维随机变量(X，Y)的联合分布律及关于X和关于Y的边缘分布律中的部分数值.试将其余数值填入表中的空白处.
    　　


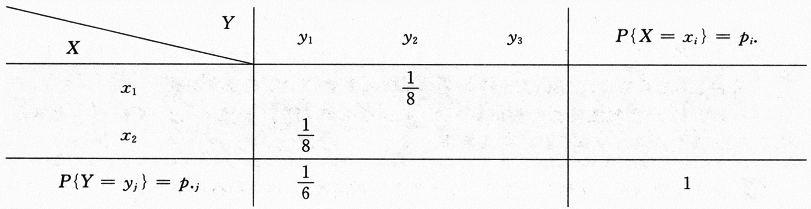    答案：
    解析：
    当离散型随机变量(X，Y)中X与Y相互独立时，有进一步就有，也就是说(X，Y)的分布律中，当X，Y独立就对应各行成比例.有了这一点再加上边缘分布性质，就能很快解得

  • 第19题：

    设二维随机变量(X，Y)在区域上服从均匀分布，令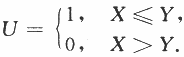
    　　(Ⅰ)写出(X，Y)的概率密度；
    　　(Ⅱ)请问U与X是否相互独立？并说明理由；
    　　(Ⅲ)求Z=U+X的分布函数F(z).


    答案：
    解析：

  • 第20题：

    设随机变量X服从指数分布，则随机变量Y＝min(X，2)的分布函数()。

    A.是连续函数
    B.至少有两个间断点
    C.是阶梯函数
    D.恰好有一个间断点

    答案：D
    解析：

  • 第21题：

    下列选项中正确的是（）。

    • A、两个泊松分布之差还是泊松分布
    • B、若两个二维分布有相同的边缘分布，则它们一定相同
    • C、若X为随机变量且X2服从χ2分布，则X服从正态分布
    • D、任意两个分布函数之和一定还是分布函数
    • E、以上选项都不正确

    正确答案:E

  • 第22题：

    设X1，X2是任意两个相互独立的连续型随机变量，它们的概率密度分别为f1（x）与f2（x），分布函数分别为F1（x）与F2（x），则（）

    • A、f1（x）+f2（x）必为某一随机变量的概率密度
    • B、f1（x）f2（x）必为某一随机变量的概率密度
    • C、F1（x）+F2（x）必为某一随机变量的分布函数
    • D、F1（x）F2（x）必为某一随机变量的分布函数

    正确答案:D

  • 第23题：

    如果两个随机变量不相关，则这两个随机变量一定相互独立。


    正确答案:错误

  • 第24题：

    多选题
    对随机变量的分布列、密度函数与分布函数，下列表述中正确的有（　　）。[2008年真题]
    A

    用分布列和密度函数描述离散随机变量的分布

    B

    用分布列和分布函数描述离散随机变量的分布

    C

    用分布列和分布函数描述连续随机变量的分布

    D

    用密度函数和分布函数描述连续随机变量的分布

    E

    用密度函数和分布函数描述离散随机变量的分布


    正确答案： B,C
    解析：
    离散随机变量的分布可用分布列表示。作为一个分布，满足以下两个条件：pi≥0，p1+p2+…+pn=1，满足这两个条件的分布称为离散分布，这一组pi又称为分布的概率函数。即用分布列和分布函数来描述离散随机变量分布。连续随机变量X的分布可用概率密度函数p（x）表示，连续随机变量X的分布函数F（x）可用其密度函数算得。反之，概率密度函数p（x）也可从分布函数F（x）求出。即用密度函数和分布函数来描述连续随机变量的分布。

相关内容