12、将一棵树转成二叉树，根结点一定没有右子树。

A、没有左子树

B、没有右子树

C、所有的节点都没有左子树

D、所有的节点都没有右子树

二叉树是结点的有限集合，这个有限集合或者为( ) ，或者由一个根结点及两棵不相交的、分别称作为根的左子树和右子树的二叉树组成。

在非空二叉树的中序遍历序列中，二叉树的根结点的左边(40)。

A．只有左子树上的所有结点

B．只有左子树上的部分结点

C．只有右子树上的所有结点

D．只有右子树上的部分结点

一棵二叉树满足下列条件：对任一结点，若存在左、右子树，则其值都小于它的左子树上所有结点的值，而大于右子树上所有结点的值。现采用【 】遍历方式就可以得到这棵二叉树所有结点的递增序列。

A．先根

B．中根

C．后根

D．层次

A、没有左子树

B、没有右子树

C、左右子树都有

D、视树的形态而定

下图所示平衡二叉树(树中任一结点的左右子树高度之差不超过1)中，结点A的右子树AR高度为h，结点B的左子树BL高度为h，结点C的左子树CL、右子树CR高度都为h-1。若在CR中插入一个结点并使得CR的高度增加1，则该二叉树(61)。

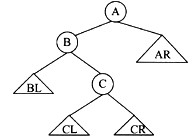
A．以B为根的子二叉树变为不平衡

B．以C为根的子二叉树变为不平衡

C．以A为根的子二叉树变为不平衡

D．仍然是平衡二叉树

阅读以下说明和C语言函数，将应填入(n)处的字句写在答题纸的对应栏内。

【说明】

一棵非空二叉树中“最左下”结点定义为：若树根的左子树为空，则树根为“最左下”结点；否则，从树根的左子树根出发，沿结点的左

子树分支向下查找，直到某个结点不存在左子树时为止，该结点即为此二叉树的“最左下”结点。例如，下图所示的以 A为根的二叉树的“最

左下”结点为D，以C为根的子二叉树中的“最左下”结点为C。

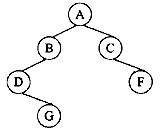
二叉树的结点类型定义如下：

typedef stmct BSTNode{

int data；

struct BSTNode*lch,*rch；//结点的左、右子树指针

}*BSTree；

函数BSTree Find Del(BSTree root)的功能是：若root指向一棵二叉树的根结点，则找出该结点的右子树上的“最左下”结点*p，并从

树于删除以*p为根的子树，函数返回被删除子树的根结点指针；若该树根的右子树上不存在“最左下”结点，则返回空指针。

【函数】

BSTrce Find_Del(BSTreeroot)

{ BSTreep,pre；

if ( !root ) return NULL； /*root指向的二叉树为空树*/

(1)； /*令p指向根结点的右子树*/

if ( !p ) return NULL；

(2)； /*设置pre的初值*/

while(p-＞lch){ /*查找“最左下”结点*/

pre=p；p=(3)；

}

if ((4)==root) /*root的右子树根为“最左下”结点*/

pre-＞rch=NULL；

else

(5)=NULL； /*删除以“最左下”结点为根的子树*/

reurn p；

}