有一片均匀生长的草地，可供27头羊吃2天，或供23头羊吃j天，那么它可供21头羊吃几天?（ ）A．4天B．5天C．6天D．7天

题目

有一片均匀生长的草地，可供27头羊吃2天，或供23头羊吃j天，那么它可供21头羊吃几天?（ ）

A．4天

B．5天

C．6天

D．7天

相似考题

1.有三块草地，面积分别是4亩、8亩、10亩。草地上的草一样多，而且按相同的速度均匀生长，第一块草地可供24头牛吃6周，第二块草地可供36头牛吃12周。问第三块草地可供50头牛吃几周?A．6B．9C．3D．7

2.牧场上有一片青草，草每天以均匀的速度生长，这些草供给20头牛吃，可以吃20天；供给100头羊吃，可以吃12天。如果每头牛每天的吃草量相当于4只羊一天的吃草量，那么20头牛，100只羊同时吃这片草，可以吃几天?（）A.2B.4（8/13）C.6（7/12）D.8

3.由于天气逐渐变冷，牧场上的草每天以均匀的速度减少。经计算，牧场上的草可供20头牛吃5天，或供16头牛吃6天，那么可供11头牛吃（ ）天。A．12B．10C．8D．6

4.牧场有一片青草，每天生成速度相同。现在这片牧场可供16头牛吃20天，或者供80只羊吃12天，如果一头牛一天吃草量等于4只羊一天的吃草量，那么10头牛与60只羊一起吃可以吃多少天？（ ）A.7B.8C.12D.15

更多“有一片均匀生长的草地,可供27头羊吃2天,或供23头羊吃j天,那么它可供21头羊吃几天?( ) ”相关问题

  • 第1题：

    牧场上有一片青草，每天牧草都匀速生长。这片牧草可供10头牛吃20天，或者可供15头牛吃10天。问：可供25头牛吃几天？（ ）

    A．5

    B．10

    C．15

    D．20


    正确答案：A
    设1头牛1天吃的草为1份，10头牛20天吃10×20=200(份)，15头牛10天吃15×10=150(份)，这说明牧场每天新长草(200-150)÷(20-10)=5(份)。原来牧场有草(10-5)×20=100(份)，吃新草的牛需要5÷1=5(头)，吃旧草的牛有25—5=20(头)，则吃完草的时间为100÷20=5(天)。

  • 第2题：

    秋冬之际，由于天气逐渐变冷，牧场上的草以固定的速度在减少。已知一个牧场上的草可供45头牛吃4天或可供25头牛吃6天。照此计算，这个牧场可供几头牛吃10天?


    答案：
    解析：
    假设每天每头牛吃1份草， 每天牧场草减少的份数：(45×4—-25×6)÷(6-4)=15，
    牧场原有牧草的份数：45×4+15×4=240，
    10天牧场共能提供牧草的份数：240-15×10=90，
    90+10=9．故这个牧场可供9头牛吃10天。

  • 第3题：

    有三块草地，面积分别是4亩、8亩、10亩。草地上的草一样厚，而且长得一样快，第一块草地可供24头牛吃6周，第二块草地可供36头牛吃12周。问第三块草地可供50头牛吃几周?（）
    A.6
    B.9
    C.3
    D.7


    答案：B
    解析：
    草地面积不同，化简为相同的草地面积，可将原问题转化为：“一亩草地可供6头牛吃6周，4．5头牛吃12周。问可供5头牛吃多少周?”
    设每头牛每周的吃草量为1，则每亩地每周的长草量为(4．5×12—6×6)÷(12—6)=3，每亩地最初的草量为(6—3)×6=18，故50头牛在第三块草地可以吃18÷(5—3)=9周。

  • 第4题：

    某天然牧场有一片生长均匀的牧草，10只羊可吃8天，8只羊可吃12天，那么6只羊可吃多少天?（ ）

    A．16

    B．20

    C．24

    D．28


    正确答案：C
    设每天新增草量可供X只羊吃1天，另外设这片牧草可供6只羊吃y天。则有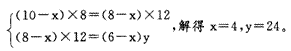

  • 第5题：

    牧场上长满牧草，每天牧草都均匀生长。这片牧场可供10头牛吃20天，可供15头牛吃10天，则可供25头牛吃几天?（）[银行真题]
    A.5
    B.7
    C.6
    D.8


    答案：A
    解析：
    此题为典型牛吃草问题。牛吃草问题只需抓住核心公式即可。
    假设每头牛每天吃的草为1，每天的长草量为x，最初的牧场总草量为y。则：
    (10-x)×20=y
    (15-x)×10=y
    解得：x=5，y=100
    现在25头牛可以吃100÷(25—5)=5天．
    所以正确答案为A。

相关内容