甲、乙两个文艺队参加大型文艺汇演,甲队的人数是乙队的55%。根据节目需要,现从乙队抽出20人到甲队,此时乙队比甲队多68人,则甲队原有人数是( )。A.132B.112C.172D.240
题目
甲、乙两个文艺队参加大型文艺汇演,甲队的人数是乙队的55%。根据节目需要,现从乙队抽出20人到甲队,此时乙队比甲队多68人,则甲队原有人数是( )。
A.132
B.112
C.172
D.240
相似考题
更多“甲、乙两个文艺队参加大型文艺汇演,甲队的人数是乙队的55%。根据节目需要,现从乙队抽出20 ”相关问题
-
第1题:
甲、乙两个工程队,甲队的人数是乙队的70%。根据工程需要,现从乙队抽出40人到甲队,此时乙队比甲队多136人,则甲队原有人数是( )
A.504人 B.620人 C.630人 D.720人
正确答案:A
设乙队为x人,则甲为0.7x人, x-40=0.7x +40 + 136 , x =720人
甲为720×0.7 =504人。
-
第2题:
甲、乙两个小分队的人数之和在90到110之间,如果从甲队调一定人数给乙队,则乙队的人数就是甲队的2倍;如果乙队调同样的人数给甲队,则甲队的人数就是乙队的3倍。问甲队调多少人给乙队之后,乙队的人数是甲队的5倍()A、85
B、90
C、95
D、100答案:D解析:本题考查常规计算。解法一:由于甲乙总人数不变,第一种情况乙队人数就是甲队的2倍,可知总人数是3的倍数,第二种情况甲队人数是乙队的3倍,可知总人数是4的倍数,则总人数是12的倍数,人数取值范围为90-110,可知总人数为96或者108。若总人数为96,代入排除法。A项,调动之前甲为96/6+18=34人,则乙为62人,不满足乙调2人给甲,甲是乙的3倍,排除;B项,调动之前甲为96/6+24=40人,则乙为56人,不满足乙调8人给甲,甲是乙的3倍,排除;C项,调动之前甲为96/6+30=46人,则乙为50人,不满足乙调14人给甲,甲是乙的3倍,排除;D项,调动之前甲为96/6+36=52人,则乙为44人,满足甲调20人给乙,乙是甲的2倍,也满足乙调20人给甲,甲是乙的3倍,D选项正确。解法二:方程法,假设甲乙共有96人,设调动x人,甲原有y人,则96-y+x=2(y-x),y+x=3(96-y-x),解得x=20,y=52,甲有52人,乙有96-52=44人,设甲队调z人去乙,乙队人数是甲队的5倍,44+z=5(52-z),得z=36。故本题答案为D选项。
【知识点】常规计算 -
第3题:
甲、乙两个文艺队参加大型文艺汇演,甲队的人数是乙队的55%。根据节目需要,现从乙队抽出20人到甲队,此时乙队比甲队多68人,则甲队原有人数是( )。A. 132
B. 112
C. 172
D. 240答案:A解析:根据题意,乙队比甲队多20×2+68=108(人),占乙队的1 -55%= 45%,则乙队有108÷45%=240(人),曱队有240×55 % =132(人),故本题正确答案为A。 -
第4题:
A、B两项工程分别由甲、乙两个队来完成。在晴天甲队完成A工程需要12天,乙队完成B工程需要15天;在雨天甲队效率下降40%,乙队效率下降10%,现在两队同时开工,并且同时完成了任务,问施工期间有多少个雨天?( )A.8
B.9
C.10
D.11答案:C解析:
-
第5题:
一项工程,乙队先独做4天,继而甲、丙两队合做6天,剩下的工程甲队又独做9天才全部完成,已知乙队完成的是甲队的1/3,丙队完成的是乙队的2倍,如果甲单独做,需要( )天A.18
B.24
C.28
D.30
E.45答案:D解析:
-
第6题:
已知“甲队可能会战胜乙队”,可以推出()
- A、甲队必然战胜乙队
- B、并非“甲队必然不会战胜乙队”
- C、并非“甲队可能不会战胜乙队”
- D、并非“甲队必然会战胜乙队
正确答案:B -
第7题:
与“若甲队不是冠军,则乙队是冠军”等值的命题有()。
- A、只有乙队是冠军,甲队才不是冠军
- B、只有甲队是冠军,乙队才不是冠军
- C、如果乙队不是冠军,那么甲队是冠军
- D、并非甲、乙两队都不是冠军
- E、或者乙队是冠军,或者甲队是冠军
正确答案:A,B,C,D,E -
第8题:
正确的连续请求暂停与换人是()
- A、甲队暂停,乙队暂停,甲队换人
- B、甲队换人,乙队换人,甲队换人
- C、甲队换人,乙队暂停,甲队换人
正确答案:C -
第9题:
乙队过了比赛时间15分钟未能出场参加比赛,应判乙队弃权,甲队获胜。
正确答案:正确 -
第10题:
单选题正确的连续请求暂停与换人是()A甲队暂停,乙队暂停,甲队换人
B甲队换人,乙队换人,甲队换人
C甲队换人,乙队暂停,甲队换人
正确答案: A解析: 暂无解析 -
第11题:
单选题2014年索契冬奥会的男子冰壶项目,甲队和乙队都进入了前八强,关于甲、乙两队是否最终能够夺得奖牌,有如下断言。Ⅰ.甲、乙两队至少有一队能夺得奖牌。Ⅱ.甲队不一定夺得奖牌。Ⅲ.乙队夺得了奖牌。Ⅳ.甲队不可能夺不到奖牌。已知以上断言有两句为真,两句为假,由此可以推知:( )A甲队夺得了奖牌,乙队未夺得
B甲、乙两队都夺得了奖牌
C甲、乙两队都没夺得奖牌
D乙队夺得了奖牌,甲队未夺得
正确答案: D解析: -
第12题:
单选题已知“甲队可能会战胜乙队”,可推出()A甲队必然会战胜乙队
B并非“甲队必然不会战胜乙队”
C并非“甲队可能不会战胜乙队”
D并非“甲队必然会战胜乙队
正确答案: A解析: 本题考查模态方阵,可能P真时,其矛盾关系的必然非P假,则并非必然非P真,因此B项正确。 -
第13题:
某工程,甲、乙两队单独做各需要30天和20天完工。现在甲、乙两队合作,中途甲、乙两队各休息几天,因此比预定计划中的完工时间推迟了8天。又已知乙队实际工作的天数是甲队实际工作天数的2/3,乙队休息了几天?( )A.5
B.6
C.10
D.11答案:C解析:
-
第14题:
甲乙两队举行智力抢答赛,两队平均得分为92分,其中甲队平均得分为88分,乙队平均得分为94分,则甲、乙两队人数之和可能是:A.20
B.21
C.23
D.25答案:B解析:解法一:
第一步,本题考查平均数问题,用方程法计算。
第二步,设甲、乙两队人数分别为x、y,由题意可列式92(x+y)=88x+94y,解得2x=y,则甲、乙两队人数之比为1∶2,故总人数应是3的倍数,只有B选项符合。
因此,选择B选项。
解法二:
第一步,本题考查平均数问题,用十字交叉法解题。
第二步,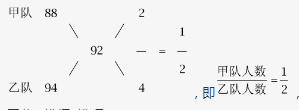
故总人数应是3的倍数,只有B选项符合。 -
第15题:
甲、乙两队单独完成某项工程分别需要10天、17天。甲队与乙队按天轮流做这项工程,甲队先做,最后是哪队第几天完工?A.甲队第11天
B.甲队第13天
C.乙队第12天
D.乙队第14天答案:B解析:
第一步,本题考查工程问题,用赋值法解题。
第二步,赋值工作总量为170(10和17的公倍数),那么甲的效率为17,乙的效率为10,那么一个周期即甲乙各做一天完成10+17=27,170÷27=6……8,即需要6个周期,还剩8个工作量,6个周期是12天,结束后第13天该甲继续做工,甲1天可完成17,那么剩下的8,甲可在第13天完成。 -
第16题:
甲、乙两个篮球队,各有若干名球员。有一天,甲队一名队员转去了乙队。从理论上来说,可能发生的情况有()A.甲队的平均身高增加,乙队的平均身高增加
B.甲队的平均身高增加,乙队的平均身高下降
C.甲队的平均身高下降,乙队的平均身高增加
D.甲队的平均身高下降,乙队的平均身高下降答案:A,B,C,D解析:描述统计;集中量数;算术平均数。 B、C是很容易想到的,但很多人想不到选项A、D。如果甲队最矮的球员都比乙队最高的球员要高,此时甲队最矮的球员转去乙队,那么两个队的平均身高都增加了。同理,如果甲队最高的球员都比乙队最矮的球员要矮,此时甲队最高的球员转去乙队,那么两个队的平均身高都下降了。因此A、B、C、D都要选。出这个题是为了教你一种思维方式:遇到棘手的问题(不论是考试中的选择题还是现实中的问题),不妨从极端情况来考虑,这样思维就会开阔很多。 -
第17题:
甲、乙两队合作一项工程,按原来的工作效率,甲队单独完成比乙队单独完成少用了3天;现在甲队提高工效20%,乙队提高工效25%;这样甲队单独完成只比乙队单独完成少用2天。如果工作效率提高后,先由乙队单独做1天,然后两队合作,还需多少天完成?A.4
B.5
C.6
D.7答案:B解析:设按原来的工作效率甲单独完成需要x天,则乙单独完成需要(x+3)天,提高效率后,甲
-
第18题:
已知“甲队可能会战胜乙队”,可推出()
- A、甲队必然会战胜乙队
- B、并非“甲队必然不会战胜乙队”
- C、并非“甲队可能不会战胜乙队”
- D、并非“甲队必然会战胜乙队"
正确答案:B -
第19题:
“并非甲、乙两队都是冠军”的意思是“如果甲队不是冠军,那么乙队一定是冠军”。
正确答案:错误 -
第20题:
下列换人属于合法替换的是()。
- A、甲队换人后,乙队换人,甲队随即再次换人
- B、甲队换人后,乙队要求暂停,暂停完毕后乙队要求换人
- C、乙队要求暂停,甲队要求换人,裁判鸣哨发球前甲队再次要求换人
正确答案:B -
第21题:
以“如果甲队战胜乙队,那么,甲队夺得冠军”为前提进行假言三段论推理,可推出的结论是()。
- A、并非甲队夺得冠军
- B、并非甲队战胜乙队
- C、甲队夺得冠军
- D、乙队夺得冠军
- E、甲队战胜乙队
正确答案:B,C -
第22题:
多选题以“如果甲队战胜乙队,那么,甲队夺得冠军”为前提进行假言三段论推理,可推出的结论是()。A并非甲队夺得冠军
B并非甲队战胜乙队
C甲队夺得冠军
D乙队夺得冠军
E甲队战胜乙队
正确答案: B,D解析: 暂无解析 -
第23题:
单选题已知“甲队可能会战胜乙队”,可以推出()A甲队必然战胜乙队
B并非“甲队必然不会战胜乙队”
C并非“甲队可能不会战胜乙队”
D并非“甲队必然会战胜乙队
正确答案: B解析: 由“可能P”可推出“不必然非P”即“并非必然非P”。由此,已知“甲队可能会战胜乙队”可推出并非“甲队必然不会战胜乙队”。
