：某服装厂有甲、乙、丙、丁四个生产组，甲组每天能缝制8件上衣或10条裤子；乙组每天能缝制9件上衣或12条裤子；丙组每天能缝制7件上衣或11条裤子；丁组每天能缝制6件上衣或7条裤子。现在上衣和裤子要配套缝制（每套为一件上衣和一条裤子），则7天内这四个组最多可以缝制衣服（ ）。A．110套B．115套C．120套D．125套

题目

：某服装厂有甲、乙、丙、丁四个生产组，甲组每天能缝制8件上衣或10条裤子；乙组每天能缝制9件上衣或12条裤子；丙组每天能缝制7件上衣或11条裤子；丁组每天能缝制6件上衣或7条裤子。现在上衣和裤子要配套缝制（每套为一件上衣和一条裤子），则7天内这四个组最多可以缝制衣服（ ）。

A．110套

B．115套

C．120套

D．125套

相似考题

1.有甲、乙、丙、丁四个数，已知甲的8%是9，乙的9%是10，丙的10%是11，丁的11%是12，甲、乙、丙、丁四个数中最小的数是：A.甲 B.乙 C.丙 D.丁

2.1991年李某死亡，对所遗财产无遗嘱。李有二子一女，长子1949年死亡，生一子甲，甲1980年死亡，遗一女乙，次子1978年死亡，遗一女丙，女儿1976年死亡，收养一子丁，现乙、丙、丁为继承发生争执（）。A.乙、丙、丁都有继承权B.乙丙能继承，丁不能C.丙能继承，乙、丁不能D.只有丁有继承权

3.某企业采用成对比较法进行岗位评价，将所有岗位进行成对比较，结果是乙的工作价值高于甲、丙、丁；甲的价值低于乙，高于丙、丁；丙的价值低于甲、乙，高于丁；丁的价值低于甲、乙、丙。那么将四个岗位的工作价值从高到低排序为（ ）。A．丙、甲、乙、丁B．乙、甲、丙、丁C．甲、乙、丙、丁D．丁、乙、甲、丙

4.某企业有四个岗位利用成对排列法进行排列，结果是丁高于甲、乙、丙；乙低于甲、丙、丁；丙高于乙，但低于甲、丁，甲、乙、丙、丁的岗位评价由高至低是（）。A 乙甲丙丁B 丙甲乙丁C 甲乙丙丁D 丁甲丙乙

参考答案和解析
正确答案：D

当甲、乙、丙、丁生产上衣的天数按照7，3，0，7的方案分配时可生产125套衣服，故本题选D。

更多“:某服装厂有甲、乙、丙、丁四个生产组,甲组每天能缝制8件上衣或10条裤子;乙组每天能缝制9件上 ”相关问题

  • 第1题：

    在四个域甲、乙、丙、丁，甲信任乙，乙信任丙，丙信任丁，甲信任丙，乙信任丁，则在丁中创建的全局组用户能访问域中的哪些资源()。

    A、甲、乙、丙、丁

    B、乙、丙、丁

    C、丙、丁

    D、丁


    参考答案：B

  • 第2题：

    某服装店有甲、乙、丙、丁四个缝制小组。甲组每天能缝制5件上衣或6条裤子：乙组每天能缝制6件上衣或7条裤子：丙组每天能缝制7件上衣或8条裤子；丁组每天能缝制8件上衣或9条裤子。每组每天要么缝制上衣，要么缝制裤子，不能弄混。订单要求上衣和裤子必须配套（每套衣服包括一件上衣和一条裤子）。做好合理安排，该服装店15天最多能缝制（ ）套衣服。

    A.208B.209C.210D.211


    正确答案：D

  • 第3题：

    已知某工厂有28名工人，每个工人每天可缝制12顶帽子或18个肩章，已知一顶帽子需和两个肩章配套，则多少人缝制帽子时，可使帽子和肩章每天的产量刚好配套?()

    A.12
    B.14
    C.16
    D.18

    答案：A
    解析：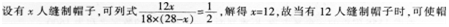

    子和肩章每天的产量刚好配套。

  • 第4题：

    某单位春季植树100棵，前2天安排乙组植树，其余任务由甲、乙两组共用3天完成，已知甲组每天比乙组多植树4棵，则甲组每天植树（ ）棵

    A.11
    B.12
    C.13
    D.15
    E.17

    答案：D
    解析：
    设甲组每天植树x棵，乙组植树x-4棵，可知：3x+5（x-4）=100=>x=15

  • 第5题：

    某服装店有甲、乙、丙、丁四个缝制小组。甲组每天能缝制5件上衣或6条裤子：乙组每天能缝制6件上农或7条裤子：丙组每天能缝制7件上衣或8条裤子；丁组每天能缝制8件上衣或9条裤子。每组每天要么缝制上衣，要么缝制裤子，不能弄混。订单要求上衣和裤子必须配套（每套衣服包括一件上衣和一条裤子）。做好合理安排，该服装店15天最多能缝制（ ）套衣服。

    A. 208
    B. 209
    C. 210
    D. 211

    答案：D
    解析：
    由题目：各个小组生产上衣和裤子的工作效率比： 甲：5：6乙：6：7 丙：7：8丁：8：9 依次增大。因为上衣生产的慢所以 所以让丁（最快）生产15天上衣：8*15＝120甲也生产15天裤子：15*6＝90乙生产15天裤子：15*7=105；设丙生产x天裤子： 105＋90＋X*8＝120＋7*（15-x）X＝2 所以生产最多：90＋105＋8*2＝211

  • 第6题：

    某木场有甲，乙，丙三位木匠师傅生产桌椅，甲每天能生产12张书桌或13把椅子；乙每天能生产9张书桌或12把椅子，丙每天能生产9张书桌或15把椅子，现在书桌和椅子要配套生产（每套一张书桌一把椅子），则7天内这三位师傅最多可以生产桌椅（）套。

    A. 116
    B. 129
    C. 132
    D. 142

    答案：B
    解析：
    统筹问题。甲、乙、丙生产桌子的效率分别为12、9、9，生产椅子的效率分别为13、12、15，根据效率差最高原则，故应该选甲全部生产书桌，丙全部生产椅子。甲生产桌子12×7=84张，丙生产椅子15×7=105张。乙就应该做一部分椅子，做一部分书桌。设乙生产书桌x天，则乙生产椅子（7-x）天，根据题意书桌数等于椅子数，有方程84+9x=105+12（7-x），解得x=5天。方程左右都是生产的最多的桌椅套数，因此最多可以生产桌椅84+9×5=84+45=129套。故选择B。

  • 第7题：

    1991年李某死亡，对所遗财产无遗嘱。李有二子一女，长子1949年死亡，生一子甲，甲1980年死亡，遗一女乙，次子1978年死亡，遗一女丙，女儿1976年死亡，收养一子丁，现乙、丙、丁为继承发生争执（）。

    • A、乙、丙、丁都有继承权
    • B、乙丙能继承，丁不能
    • C、丙能继承，乙、丁不能
    • D、只有丁有继承权

    正确答案:A

  • 第8题：

    甲组和乙组共有86人，乙组和丙组共有88人，丙组和丁组共有91人，问甲组和丁组共有多少人( )

    • A、80
    • B、87
    • C、89
    • D、90

    正确答案:C

  • 第9题：

    单选题
    服装厂的工人每人每天可以生产4件上衣或7条裤子，一件上衣和一条裤子为一套服装。现有66名工人生产，每天最多能生产多少套服装？（）
    A

    168

    B

    188

    C

    218

    D

    246


    正确答案： D
    解析： 由题意，每个工人每天可以生产的上衣和裤子的比例为4：7，要使生产的服装套数更多，则最终生产的上衣和裤子数量要相同，所以生产上衣和裤子的工人比例为7：4，有66名工人，则生产上衣的工人数量为66×7/11=42，生产裤子的工人数量为66×4/11=24，生产服装数量最多等于42×4=168。故正确答案为A。

  • 第10题：

    某服装厂有甲、乙、丙、丁四个生产组，甲组每天能缝制8件上衣或10条裤子；乙组每天能缝制9件上衣或12条裤子；丙组每天能缝制7件上衣或11条裤子；丁组每天能缝制6件上衣或7条裤子。现在上衣和裤子要配套缝制（每套为一件上衣和一条裤子），则7天内这四个组最多可以缝制衣服（ ）。

    A．110套

    B．115套

    C．120套

    D．125套


    答案：D。
    【解析】

    常规解法：这是一个统筹问题，要四个组生产的衣服最多，显然应各自发挥其所长。比较四个小组的生产速度，甲、丁两生生产上衣速度相对较快；丙组生产裤子的速度较快，乙组生产速度居中。

    故应安排这七天时间，甲丁两组7天时间只生产上衣，丙组7天时间只生产裤子，乙组作调剂（最终结果为3天生产上衣、4天生产裤子）。共可生产125套衣服，选D。

    简便算法：四个组1天内全部生产上衣或裤子，则可生产30件上衣或40条裤子。如果不考虑最优，平均分配时间，则7天时间安排为4天全部生产上衣、3天全部生产裤子，共生产120套。既然要统筹考虑、优化方案，保证生产的服装最多，肯定应充分发挥各自所长（生产衣服快的只生产衣服，生产裤子快的只生产裤子，居平均水平的用来调剂），这样的生产量肯定要多于120套，只有选项D合适。

     

  • 第11题：

    演绎推理：共10题，每题给出一段陈述，这段陈述假设是正确的，不容量疑的。你根据这段陈述，选出一个答案。注意，正确的答案应与所给的陈述相符合，不需要任伺说明即可以从陈述中直接推出。

    例题：某厂有五种产品：甲、乙、丙、丁、戊。它们的年销售额之间的关系为：丙没有丁；没有乙高，戊不比丁低，而乙不如丙高。

    请问，哪种产品的年销售额最高?

    A．甲

    B．乙

    C．丁

    D．戊

    解答：从所给条件可以知道：戊＞丁＞丙＞乙＞甲。因此，正确答案为D。

    请开始答题：

    有甲、乙、丙、丁四个小组进行拔河比赛，比赛结果是：

    ①当甲、乙两组联合为一方，丙组和丁组为一方时，双方势均力敌；

    ②当甲组与丙组对调后，甲、丁两组联合战胜了乙、丙两组；

    ③甲、丙两组联合却被乙组单独一方战胜。

    下列关于甲、乙、丙、丁四个组由强到弱的排序正确的是( )

    A．甲、乙、丙、丁

    B．丙、乙、丁、甲

    C．乙、甲、丙、丁

    D．丁、乙、甲、丙


    正确答案：D
    [答案] D。解析：本题要代入法，根据题干的③可以排除AB；根据①和②，可以排除C；可见D是最合适的顺序，所以选择D。

  • 第12题：

    已知有甲、乙、丙、丁四个数，甲、乙之和大于丙、丁之和，甲、丁之和大于乙、丙之和，乙、丁之和大于甲、丙之和。根根据以上请判断这四个数谁最小？（）
    A 甲最小
    B 丙最小
    C 乙最小
    D 丁最小


    答案：B
    解析：
    第一步：整理题干信息。
    （1）甲＋乙>丙＋丁；（2）甲＋丁>乙＋丙；（3）乙＋丁>甲＋丙。
    第二步：根据信息整合。
    将不等式相加，同方向的不等号不变，（1）+（2）可得甲>丙，（2）+（3）可得丁>丙，（1）+（3）可得乙>丙，综合三个结果可知丙最小。
    故正确答案为B。

  • 第13题：

    某服装店有甲、乙、丙、丁四个缝制小组。甲组每 天能缝制5件上衣或6条裤子： 乙组每天能缝制6件上农或7条裤子：丙组每天能缝 制7件上衣或8条裤子；丁组每天能缝制8件上衣或9 条裤子。每组每天要么缝制上衣，要么缝制裤子， 不能弄混。订单要求上衣和裤子必须配套（每套衣 服包括一件上衣和一条裤子）。做好合理安排，该 服装店15天最多能缝制（ ）套衣服。

    A. 208
    B. 209
    C. 210
    D. 211

    答案：D
    解析：
    由题目：各个小组生产上衣和裤子的工作效率比：
    甲：5：6 乙：6：7 丙：7：8
    丁：8：9 依次增大。
    l 因为上衣生产的慢所以 所以让丁（最快）生产15天上衣：8*15＝120 甲也生产15天裤子：15*6＝90 乙生产15天裤子：15*7=105；
    l 设丙生产x天裤子： 105＋90＋X*8＝120＋7*（15-x） X＝2 所以生产最多：90＋105＋8*2＝211

  • 第14题：

    有甲、乙两个课外活动小组，甲组的人数是乙组的4/5，后来又从乙组调16人到甲组，这时乙组人数是甲组的3/4，甲、乙两组原来各有多少人？（ ）
    A.甲组40人，乙组50人 B.甲组80人，乙组100人
    C.甲组48人，乙组60人 D.甲组56人，乙组70人


    答案：D
    解析：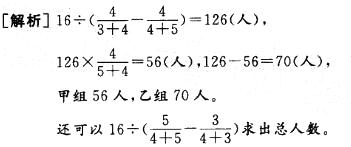

  • 第15题：

    某企业采用成对比较法进行岗位评价，将所有岗位进行成对比较，结果是乙的工作价值高于甲、丙、丁；甲的价值低于乙，高于丙、丁；丙的价值低于甲、乙，高于丁；丁的价值低于甲、乙、丙。那么将四个岗位的工作价值从高到低排序为()。

    A:丙、甲、乙、丁
    B:乙、甲、丙、丁
    C:甲、乙、丙、丁
    D:丁、乙、甲、丙

    答案：B
    解析：
    乙的工作价值高于甲、丙、丁，所以乙的工作价值最高；甲的价值低于乙，高于丙、丁，甲的工作价值排在第二位；丙的价值低于甲、乙，高于丁，丙的工作价值排在第三位；丁的价值低于甲、乙、丙，所以丁的工作价值最低。

  • 第16题：

    服装厂的工人每人每天可以生产4件上衣或7条裤子，一件上衣和一条裤子为一套服装。现有66名工人生产，每天最多能生产多少套服装？（）

    • A、168
    • B、188
    • C、218
    • D、246

    正确答案:A

  • 第17题：

    单选题
    甲组6人15天能完成的工作，乙组5人12天也能完成。乙组7人8天能完成的工作，丙组3人14天也能完成。一项工作，需要甲组9人4天完成。如果由丙组派人6天完成，丙组立该派多少人？
    A

    2

    B

    3

    C

    4

    D

    5


    正确答案： B
    解析： 暂无解析

相关内容