一批产品共50件,其中46件合格品,4件次品,从中任取3件,其中有次品的概率是多少? 次品不超过2件的概率是多少?

题目
一批产品共50件,其中46件合格品,4件次品,从中任取3件,其中有次品的概率是多少? 次品不超过2件的概率是多少?

相似考题

1.(本题满分10分) 设20件产品中有3件次品，从中任取两件，在已知其中有一件是次品的条件下，求另一件也是次品的概率．

2.在一批N个产品中有M个次品，从这批产品中任取n个产品，其中含有m个次品的概率是( )。

3.设50件产品中，45件是正品，5件是次品，从中任取3件，求其中至少有l件 是次品的概率(精确到0．01)．

4.若10个产品中有7个正品,3个次品:(1)不放回地每次从中任取一个,共取3次,求取到3个次品的概率;(2)每次从中任取一个,有放回地取3次,求取到3个次品的概率。

更多“一批产品共50件,其中46件合格品,4件次品,从中任取3件,其中有次品的概率是多少? 次品不超过2件的概率是多少? ”相关问题

  • 第1题：

    10件产品有3件次品,7件正品,每次从中任取一件,取后不放回,求下列事件的概率：
    　　(1)第三次取得次品；
    　　(2)第三次才取得次品；
    　　(3)已知前两次没有取到次品,第三次取得次品；(4)不超过三次取到次品.


    答案：
    解析：
    【解】设Ai={第i次取到次品}(i=1，2，3).
    (1)
    (2)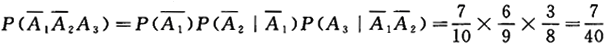（试验还没有开始，计算前两次都取不到次品，且第三次取到次品的概率）.
    (3)（已知前两次已发生的结果，唯一不确定的就是第三次）.
    (4)

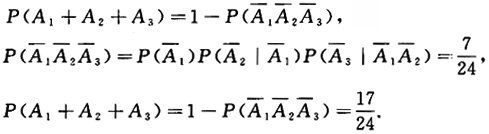
  • 第2题：

    设某批产品的次品率为0.01，现从中任取4个，则至少有一个次品的概率为0.04.


    正确

  • 第3题：

    某产品40件，其中有次品3件，现从中任取3件，取出的3件产品中所含次品数X=1的概率为（）。

    A．0.7865；

    B．0.2022；

    C．0.0112；

    D．0.0001；


    抽到的3件产品构成一样本点因为它们没有顺序的区别故样本点总数为C 40 3 ． (1)令A 1 表示“3件中恰有1件次品”．其中的一件次品可以在3件次品中任取1件有C 3 1 种取法另外2件正品可从37件正品中任取共有C 37 2 二者搭配共有C 3 1 C 37 2 种取法因此A 1 所包含的样本点数为C 3 1 C 37 2 由(1．1)式有 ． (2)令A 2 表示“3件中恰有2件次品”由(1)中的分析方法知A 2 所包含的样本点数为C 3 2 C 37 1 故 ． (3)令A 3 表示“3件全是次品”则A 3 所包含的样本点数为C 3 3 于是 ． (4)令A 4 表示“3件全是正品”A 4 所包含的样本点数为C 37 3 于是 ． (5)令A 6 表示“3件中至少有1件次品”．由于 =A 4 于是由概率的性质④ P(A 5 )=1一P( )一1一P(A 4 )≈0．213 6． 抽到的3件产品构成一样本点,因为它们没有顺序的区别,故样本点总数为C403．(1)令A1表示“3件中恰有1件次品”．其中的一件次品可以在3件次品中任取1件,有C31种取法,另外2件正品可从37件正品中任取,共有C372,二者搭配共有C31C372种取法,因此A1所包含的样本点数为C31C372,由(1．1)式有．(2)令A2表示“3件中恰有2件次品”,由(1)中的分析方法知A2所包含的样本点数为C32C371,故．(3)令A3表示“3件全是次品”,则A3所包含的样本点数为C33,于是．(4)令A4表示“3件全是正品”,A4所包含的样本点数为C373,于是．(5)令A6表示“3件中至少有1件次品”．由于=A4,于是由概率的性质④,P(A5)=1一P()一1一P(A4)≈0．2136．

  • 第4题：

    5件产品其中3件正品2件次品，从中任取3件，那么取到次品的概率是未取到次品概率的（）倍

    A．2

    B．3

    C．5

    D．9


    9

  • 第5题：

    盒中有100个零件，其中有5个次品，每次从中抽取一个，取后不放回，则第二次才取得正品的概率是多少？


    设5个产品中次品数为k，则其概率为 k=0,1，2，…，5．计算出P{X=k}，作出如下表格。 X 0 1 2 3 4 5 p k 0.5838 0.3394 0.0702 0.0064 0.00025 ≈0

相关内容