园丁将若干同样大小的花盆在平地上摆放为不同的几何图形,发现如果增加5盆,就能摆成实心正三角形,如果减少4盆,就能摆成每边多于1个花盆的实心正方形,问将现有的花盆摆成实心矩形,最外层最少有多少盆花?A.22 B.24 C.26 D.28
题目
园丁将若干同样大小的花盆在平地上摆放为不同的几何图形,发现如果增加5盆,就能摆成实心正三角形,如果减少4盆,就能摆成每边多于1个花盆的实心正方形,问将现有的花盆摆成实心矩形,最外层最少有多少盆花?
A.22
B.24
C.26
D.28
B.24
C.26
D.28
相似考题
参考答案和解析
答案:A
解析:
第一步,本题考查几何构造问题。
第二步,根据题意,增加5盆能摆成实心正三角形,摆成一个边有n个花盆的实心正三角形需要
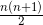
个花盆,则花盆总数为
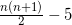
减少4盆能摆成实心正方形,说明(花盆总数-4)应该是一个平方数。采用特殊值依次代入验证,发现只有当n=9即花盆数为40时,同时满足这两个条件。那么共有40个花盆。
第三步,根据几何最值理论,当四边形面积一定时,越接近正方形,周长越短。故当矩形的两条边分别是5和8时,最外层花盆数最少,此时最外层有(8+5)×2-4=22(盆)花。
因此,选择A选项。
第二步,根据题意,增加5盆能摆成实心正三角形,摆成一个边有n个花盆的实心正三角形需要
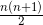
个花盆,则花盆总数为
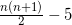
减少4盆能摆成实心正方形,说明(花盆总数-4)应该是一个平方数。采用特殊值依次代入验证,发现只有当n=9即花盆数为40时,同时满足这两个条件。那么共有40个花盆。
第三步,根据几何最值理论,当四边形面积一定时,越接近正方形,周长越短。故当矩形的两条边分别是5和8时,最外层花盆数最少,此时最外层有(8+5)×2-4=22(盆)花。
因此,选择A选项。
更多“园丁将若干同样大小的花盆在平地上摆放为不同的几何图形,发现如果增加5盆,就能摆成实心正三角形,如果减少4盆,就能摆成每边多于1个花盆的实心正方形,问将现有的花盆摆成实心矩形,最外层最少有多少盆花?”相关问题
-
第1题:
小王将棋子摆成一个空心方阵,最外层共64枚,最内层共32枚,共有多少枚?()
A.68
B.200
C.240
D.375答案:C解析:根据最外层棋子数64枚,可求出最外层每边数:64÷4+1=17枚,內层数32枚,可求出內层每边数为32÷4+1=9枚,然后用大实心方阵总数减去小实心方阵总数。所以空心方阵总数是:17×17-(9—2)×(9—2)=240枚。 -
第2题:
某单位组织员工做工间操,员工站成一个实心方阵(正方形队列)时,还多8 人,如果站成一个每边比前面多1 人的实心方阵,则还少17 人。问该单位有员工多少人?( )。A.136 人
B.152 人
C.159 人
D.177 人答案:B解析:设原方阵每边有x 人,则新方阵每边有x+1 人,由题意,2(x+1)-2x=25,解得x=12。所以共有144+8=152 人。 -
第3题:
在水泥铺装的广场上用盆花布置临时花坛,一般做法是()。
- A、带花盆摆放
- B、脱花盆摆放
- C、将花剪下摆放
- D、将花盆敲碎摆放
正确答案:A -
第4题:
用红、黄两色鲜花组成的实心方阵(所有花盆大小完全相同),最外层是红花,从外往内每层按红花、黄花相间摆放。如果最外层一圈的正方形有红花44盆,那么完成造型共需黄花()。
- A、48盆
- B、60盆
- C、72盆
- D、84盆
正确答案:B -
第5题:
求救信号中,如何摆放三堆火堆是国际通行的方式?()
- A、摆成一直线
- B、摆成曲线
- C、摆成三角形
- D、不规则摆放
正确答案:C -
第6题:
单选题某学校在做广播体操时,三年级的学生站成一个实心方阵时(正方形队列)时,还多10人,如果站成一个每边多1人的实心方阵,则还缺少15人,问三年级的学生共有多少人?( )A130
B146
C154
D160
正确答案: A解析:
设最初方阵一边站x个人,则有x2+10=(x+1)2-15,解得x=12。三年级学生共有144+10=154人。 -
第7题:
单选题用红、黄两色鲜花组成的实心方阵(所有花盆大小完全相同),最外层是红花,从外往内每层按红花、黄花相间摆放。如果最外层一圈的正方形有红花44盆,那么完成造型共需黄花()。A48盆
B60盆
C72盆
D84盆
正确答案: D解析: 方阵问题。在方阵中,相邻两层之间相差8,即外圈人数总是比内圈人数多8,那么相隔一圈则相差16,并且成等差数列。题目中最外层红花为44,则次外层黄花为36,可知所需黄花总数为36+20+4=60(盆)。故选B。 -
第8题:
用红、黄两色鲜花组成的实心方阵(所有花盆大小完全相同),最外层是红花,从外往内每层按红花、黄花相间摆放。如果最外层一圈的正方形有红花44盆,那么完成造型共需黄花:A.48 盆
B.60 盆
C.72 盆
D.84 盆答案:B解析:方阵每层盆数=4x(每边盆数-1),则该方阵最外层每边盆数为12。摆黄花的层,每边有10,6,2 盆。故共有
4x(10+6+2)-4x3=60 盆黄花。 -
第9题:
某部队阅兵,其队形为若干层的中空方阵,最外层人数为26人,现在临时决定改成实心方阵,发现现有人员刚好组成十多层的实心方阵,问这个方阵有多少人?( )
A. 100 B. 196 C. 484 D. 576答案:D解析:[解析]仔细分析题意可知,方阵数为平方数,且与:某个平方和的和为26的平方,代入验证,A项和D项符合,再注意到题干条件为十多层的方阵,故选D。 -
第10题:
盆花生产中如何选择花盆?
正确答案: 盆花生产中花盆选择常依花卉的种类、植株的高矮和栽培目的不同而分别选用。在选择花盆时,要注意以下几点:
首先,要考虑适用性。即被选择的花盆是否能满足花卉生长发育的需要,否则不能采用。
其次,要考虑美观性。所选择的花盆要适合盆花的摆放或陈列,最好能起到画龙点睛、衬托盆花的作用。
第三,要考虑实用性,目前,盆花生产一般都具有一定的规模,因此,在选择花盆时,一定要对盆花的运输和花盆的损坏等因素充分考虑。
第四,要考虑经济性,要尽量选择价廉物美的花盆,以便降低盆花的生产成本。 -
第11题:
若干名文艺战士进行舞蹈彩排,一会儿站成(前后、左右对正)实心正方形,一会儿又站成(插缝)实心正三角形。站成正三角形时比站成正方形每边多两个人。则彩排的战士人数是()
- A、49
- B、34
- C、36
- D、38
正确答案:C -
第12题:
单选题五年级学生分成两队参加广播操比赛,排成甲、乙两个实心方阵,其中甲方阵最外层每边的人数为8。如果两队合并,可以另排成一个空心的丙方阵,丙方阵最外层每边的人数比乙方阵最外层每边的人数多4人,且甲方阵的人数正好填满丙方阵的空心。五年级一共有多少人?( )A200
B236
C260
D288
正确答案: B解析:
空心的丙方阵人数=甲方阵人数+乙方阵人数,若丙方阵为实心的,那么实心的丙方阵人数=2×甲方阵人数+乙方阵人数,即实心丙方阵比乙方阵多2×2=128人。丙方阵最外层每边比乙方阵多4人,则丙方阵最外层总人数比乙方阵多4×4=16人,即多了16÷8=2层。这两层的人数即为实心丙方阵比乙方阵多的128人,则丙方阵最外层人数为(128+8)÷2=68人,丙方阵最外层每边人数为(68+4)÷4=18人。那么,共有182-82=260人。 -
第13题:
单选题园丁将若干同样大小的花盆在平地上摆放为不同的几何图形,发现如果增加5盆,就能摆成实心正三角形;如果减少4盆,就能摆成每边多于1个花盆的实心正方形。问将现有的花盆摆成实心矩形,最外层最少有多少盆花?( )A28
B26
C24
D22
正确答案: D解析:
根据题意可得,增加5盆能摆成实心正三角形,摆成一个边有n个花盆的实心正三角形需要n(n+1)÷2个花盆,则花盆总数为n(n+1)÷2-5,减少4盆能摆成实心正方形,说明(花盆总数-4)应该是一个平方数。采用特殊值依次代入验证,发现当n=9,即花盆数为40时,满足条件。根据数学知识“当a×b为定值时,a与b越接近,其和越小”,则当a=8、b=5时,其长宽和最小。对最外层花盆计数时,每个端点的花盆会重复计数,故最外层的花盆总数=2(a+b)-4=26-4=22(盆)。因此答案选D。
