两张相同尺寸的长方形纸片，分别被甲、乙两人裁剪成两片。甲裁得两个周长为40cm 的矩形，而乙裁得两个周长为50cm的矩形。问被裁减的长方形纸片的原始周长为： A.50cm B.60cm C.80cm D.90cm

题目
两张相同尺寸的长方形纸片，分别被甲、乙两人裁剪成两片。甲裁得两个周长为40cm 的矩形，而乙裁得两个周长为50cm的矩形。问被裁减的长方形纸片的原始周长为：

A.50cm
B.60cm
C.80cm
D.90cm
相似考题

1.当x=_________时，矩形PMCN的周长是14；

2.周长为400米的圆形跑道上，有相距100米的A．B两点，甲、乙两人分别从A．B两点同时相背而跑，两人相遇后，乙即转身与甲同向而跑，当甲跑到A时，乙恰好跑到B。如果以后甲、乙跑的速度和方向都不变，那么甲追上乙时，甲从出发开始，共跑了（ ）米。A．600B．800C．900D．1 000

3.如图，甲、乙、丙、丁四个长方形拼成正方形 EFGH，中间阴影为正方形。已知，甲、乙、丙、丁四个长方形面积的和是 32cm2，四边形 ABCD 的面积是 20cm2。问甲、乙、丙、丁四个长方形周长的总和是( )。（图略）A.32cmB.56cmC.48cmD.68cm

4.冲裁力是指冲裁时,材料对凸模的()其大小与材质板厚零件的周长有关。A.最大抗力B.作用力C.反作用力D.附加压力

参考答案和解析
答案：B
解析：
如图，设原纸片边长为2a和2b厘米，则2a+4b=40,4a+2b=50。两式相加得6a+6b=90,原纸片周长为4a+4b=90÷6x4=60厘米，选B。

更多“两张相同尺寸的长方形纸片，分别被甲、乙两人裁剪成两片。甲裁得两个周长为40cm 的矩形，而乙裁得两个周长为50cm的矩形。问被裁减的长方形纸片的原始周长为： ”相关问题

  • 第1题：

    周长为400米的圆形跑道上， 有相距100米的A、B两点， 甲乙两人分别从A、B两点同时相背而跑， 两人相遇后， 乙即转身与甲同向而跑步， 当甲跑到A时， 乙恰好跑到B。如果以后甲、乙跑的速度方向都不变，那么甲追上乙时，甲从出发开始，共跑了( )米。

    A．600

    B．800

    C．900

    D．1000


    正确答案：D
    13．D【解析】乙从相遇点C跑回B点时，甲从C过B到A，他比乙多跑了100米，乙从B到C时， 甲从A到C， 说明A到C比B到C多100米， 跑道周长400米， 所以8到C是100米，A到C是200米，甲跑200米，比乙多100米。甲追上乙要多跑300=400—100(米)，所以甲要跑200X 3=600(米)，加上开始跑的一圈，甲共跑600+400=1000(米)。

  • 第2题：

    如右图甲、乙两个长方形的面积相等，甲的长与宽之比是5：4，乙的长与宽之比是6：5，甲、乙两个长方形的周长比是（）。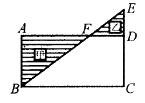



    答案：B
    解析：
    方法一：
    因为甲的长与宽之比是5 : 4，所以我们设甲的长与宽分别是5x、4x，则甲的面积为20X2，周长为18x；乙的长与宽之比是6 : 5，所以我们设乙的长与宽分别是6y，5y。则乙的面积为30y2，周长为22y；因

  • 第3题：

    一个长方形周长130厘米，如果它的宽增加1/5，长减少1/8，就得到一个相同周长的新长方形，则原长方形的面积为多少平方厘米：
    A 1000
    B 900
    C 850
    D 840


    答案：A
    解析：

  • 第4题：

    甲、乙两个长方形的面积相等，甲的长与宽之比是5：4，乙的长与宽之比是6：5，甲、乙两个长方形的周长比是


    答案：B
    解析：

  • 第5题：

    冲裁力计算公式F=KLt，故只要材质、厚度、周长相同，那么，不论零件是多复杂，冲裁力是均匀的。


    正确答案:正确

  • 第6题：

    甲、乙两人从同一地点出发，绕湖匀速背向而行，甲速度为4米/秒，乙速度为6米/秒，若干分钟后两人之间较短的弧长为湖周长的1/3，此后又过了5分钟后甲、乙两人第一次相遇，求湖周长多少千米？（）

    • A、8
    • B、9
    • C、10
    • D、12

    正确答案:B

  • 第7题：

    冲裁力是指冲裁时，材料对凸模的（）其大小与材质板厚零件的周长有关。

    • A、最大抗力
    • B、作用力
    • C、反作用力
    • D、附加压力

    正确答案:A

  • 第8题：

    画出周长为20厘米的长方形，有（）种不同画法。

    • A、4
    • B、5
    • C、6

    正确答案:B

  • 第9题：

    分别用a、b表示长方形的长和宽，C表示周长。长方形的周长公式，下面说法错误的是（）。

    • A、C=2a+b
    • B、C=2a+2b
    • C、C=（a+B.³2

    正确答案:A

  • 第10题：

    单选题
    冲裁模的凸、凹模之间，其间隙在装配时，必须将刃口处（）的间隙调整均匀，方能保证装配质量。
    A

    三分之二圆周长

    B

    整个圆周长上

    C

    半个圆周长上


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    画出周长为20厘米的长方形，有（）种不同画法。
    A

    4

    B

    5

    C

    6


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    有两个边长为整数且不相同的矩形，其中一边的长度分别为2016和2017，另一边的长度均不超过2017。已知它们的对角线长度相等，则两个矩形的周长之差为：
    A

    37

    B

    38

    C

    72

    D

    76


    正确答案： D
    解析：

  • 第13题：

    长为120米、宽为6米的长方形纸片可剪出( )个长为50厘米、宽为30厘米的长方形纸片。

    A．4500

    B．4200

    C． 4800

    D．2400


    正确答案：C
    14．C  [本题考点] 这是一道“几何”类型的题目。解此题前需要注意的一点是：题目中长度单位不统一，应将其化成统一单位。
        [解题思路] 由题童知：纸的面积为120×6=720平方米，而纸片的面积为0.5×0.3=0.15平方米，所以可剪出的纸片个数为720÷0.15=4800个，故选C。在做几何类型的题目时，特别是涉及周长、面积、体积的计算时，一定要将单位统一。

  • 第14题：

    有两个边长为整数且不相同的矩形，其中一边的长度分别为2016和2017，另一边的长度均不超过2017。已知它们的对角线长度相等，则两个矩形的周长之差为：

    A.37
    B.38
    C.72
    D.76

    答案：C
    解析：
    第一步，本题考查几何问题，属于平面几何类，用代入排除法解题。
    第二步，设两矩形另一边的长度分别为x、y，可知两矩形周长差为2×（2016＋x）－2×（2017＋y），化简为2（x－y－1），故答案为偶数，排除A。
    第三步，根据对角线长度相等得x2＋20162＝y2＋20172，化简得（x＋y）（x－y）＝4033。代入B选项，得2（x－y－1）＝38，即x－y＝20，4033不能被20整除，排除B。同理代入C选项，则x－y＝37，4033能被37整除，符合题意。代入D选项，x－y＝39，4033不能被39整除，排除D。
    因此，选择C选项。

  • 第15题：

    一个矩形的周长为100，它的面积可能是多少？

    A.600
    B.650
    C.700
    D.750

    答案：A
    解析：
    第一步，本题考查几何问题，属于几何特殊性质类。
    第二步，根据几何最值理论，周长一定的矩形，越接近正方形，面积越大。周长为100的矩形，当它为正方形时，面积最大。此时，正方形的边长为100÷4＝25，那么面积为252＝625，因此矩形的面积不能超过625，只有A选项600满足。

  • 第16题：

    某健身馆准备将一块周长为100米的长方形区域划为瑜伽场地，将一块周长为160米的长方形区域划为游泳场馆。若瑜伽场地和游泳场馆均是满足周长条件下的最大面积，问两块场地面积之差为多少平方米？

    A.625
    B.845
    C.975
    D.1150

    答案：C
    解析：
    第一步，本题考查几何问题，用几何最值理论解题。
    第二步，四边形周长固定，越接近于正方形面积则面积越大。周长为100米的四边形，当其为正方形时面积最大，故正方形边长为100÷4＝25（米），面积为252＝625（平方米）；周长为160米的四边形，当其为正方形时面积最大，故正方形边长为160÷4＝40（米），面积为402＝1600（平方米）。
    第三步，两块场地面积之差为1600－625＝975（平方米）。

  • 第17题：

    YJ27滤嘴接装机切纸轮与水松纸切刀滚切运行，水松纸被切割成纸片，其长度为烟支的周长。


    正确答案:错误

  • 第18题：

    作横截面为矩形，周长为80cm，高为30cm的容器，问容器的最大容积为多少？若油的密度为0.8g/cm3 ，求能装多少公斤的油？


    正确答案: 设该矩形的长为xcm，则宽为（40-x）cm 
    该矩形面积为：S=x（40-x）=-（x2-40x） 
    =-（x-20）2+400（cm2） 
    当x=20cm时，Smax=400cm2 
    则Vmax= Smax×30=12000（cm3） 
    油的重量G=ρV=0.8×12000=9600（g）=9.6kg 
    答：该容器的最大容积为12000cm3，能装9.6kg油。

  • 第19题：

    斐波那契推导出了椭圆周长与矩形周长的比是π：4。


    正确答案:正确

  • 第20题：

    用周长为18厘米的绳子，围成最大的长方形面积是（）平方厘米。

    • A、20
    • B、32
    • C、40

    正确答案:A

  • 第21题：

    单选题
    被积函数是常数1而被积区域是一个矩形时，二重积分的值（）。
    A

    是这个矩形线的周长

    B

    是以这个矩形为底面的锥体体积

    C

    是这个矩形的面积

    D

    是以这个矩形为底面的柱体表面积


    正确答案： B
    解析： 暂无解析

  • 第22题：

    判断题
    斐波那契推导出了椭圆周长与矩形周长的比是π：4。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第23题：

    单选题
    分别用a、b表示长方形的长和宽，C表示周长。长方形的周长公式，下面说法错误的是（）。
    A

    C=2a+b

    B

    C=2a+2b

    C

    C=（a+B.³2


    正确答案： A
    解析： 暂无解析

相关内容