设有编号为1、2、3、…、10的10张背面向上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,……,第n名(nA.2 B.4 C.6 D.8
题目
C.6 D.8
相似考题
更多“设有编号为1、2、3、…、10的10张背面向上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,……,第n名(n”相关问题
-
第1题:
按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号,当i≤n/2时,编号为i的结点的左子女的编号为
A.2i-1
B.2i
C.2i+l
D.不确定
正确答案:B
解析:根据二叉树的性质可以知道,如果对一棵有n个结点的完全二叉树的结点按层序编号,则对任意结点i(1≤i≤n)有:如果i=1,则结点i是二叉树的根,无双亲;如果i>l,则双亲PARENT(i)是结点V2。如果2i>n,则结点i无左孩子;否则其左孩子结点是2i。如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+l。本题答案为B)。 -
第2题:
阅读以下说明和C语言程序,将应填入(n)处的字句写在对应栏内。
【说明】
设有3n+2个球互连,将自然数1~3n+2分别为这些球编号,使相连的两球编号之差的绝对值正好是数列1,2,…,3n+1中的各数,如下图所示:
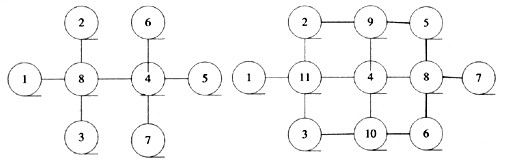
其中填自然数的思想如下;
(1)先自左向右,第1列中间1个填数,然后第2列上、下2个填数,每次2列;但若n为偶数,最后1次只排第1列中间一个数。
(2)自右向左,先右第1列中间填数;若n是奇数,再右第2列中间填数。然后依次右第1列上、下2个填数,再右第2列中间1个填数,直到左第2列为止。
【程序】
include <stdio.h>
define size 10
int a[3][size];
void main()
{
int i,k,m,n;
printf("imput the n:");
scanf("%d",&n);
k=1;
for(i=0; i<=n/2; i++)
{
a[1][2*i]=k; k++;
if((i==n/2)&& (1) ||(i<n/2))
{
a[0][2*i+1]=k;
k++;
(2)
k++;
}
}
if(n%2==1)
{
(3)
k++;
m=n;
}
else
(4)
for(i=0; i<n/2; i++)
{
a[1][m-2*i]=k; k++;
(5)
k++;
a[2][m-2*i-1]=k; k++;
}
a[1][1]=k;
printf("\n");
printf(" ");
for(i=1; i<=n; i++)
printf("%6d",a[0][i]);
printf("\n\n");
for(i=0; i<=n+1; i++)
printf("%6d",a[1][i]);
printf("\n\n");
printf(" ");
for(i=1; i<=n; i++)
printf("%6d",a[2][i]);
printf("\n");
}
正确答案:(1)(n%2==1) (2)a[2][2*i+1]=k; (3)a[1][n+1]=k; (4)m=n+1; (5)a[0][m-2*i-1]=k;
(1)(n%2==1) (2)a[2][2*i+1]=k; (3)a[1][n+1]=k; (4)m=n+1; (5)a[0][m-2*i-1]=k; 解析:本题考查C语言中具体算法的实现。
题目中要求将3n+2个球互连,并用自然数1~3n+2分别为这些球编号,使相连的两球编号之差的绝对值正好是数列1,2,…,3n+1中的各数。题目中还给出了具体的填自然数的思想。我们要完成的工作就是用C语言描述出题目中给出的思想。首先我们需要对其思想有个正确的认识,这是关键所在。
下面,我们来分析代码。结合整段程序代码,我们可以分析出,二维数组a用来存放我们要填的数字,第一维表示行数,总行数应该是3。第二维表示列数,总列数应该是n+2。其中的第(1)空所在的位置是表示一个条件判断语句的条件,在这之前已经对第1列的中间1个进行了填数,那么根据“先自左向右,第1列中间1个填数,然后第2列上、下2个填数,每次2列”的思想,再结合下面的填数程序语句,我们可以知道,此语句就是用来实现在先第1列中间1个填数后,对第2列上、下2个进行填数,每次2列这个思想的。因此,第(2)空的答案就出来了,是对第2列下(第3行)进行填数,因此,答案为“a[2][2*i+1]=k”。因为条件判断语句下面是进行了2次填数,因此可以判断n应该是个奇数,因为若n为偶数,最后1次只排第1列中间一个数,就不需要这个操作了。因此,第(1)空的作用应该是用来判断n是奇数,所以此空答案为 (n%2==1)。
第(3)空所在的位置在条件n%2==1成立的情况下才执行,条件n%2==1成立表明 n是奇数,根据若n是奇数,再右第2列中间填数的思想,我们可以知道,此处应该是对右第2列中间填数,因此,答案为a[1][n+1]=k。
第(4)空所在的位置是条件n%2==1不成立的情况下才执行,在上面我们知道 n%2==1是用来判断n是否为奇数,如果n不是奇数,我们不做什么,但为了方便后面的操作,应该将n+1的值保存起来,因此,此空的答案为m=n+1。
根据思想:若n是奇数,再右第2列中间填数。然后依次右第1列上、下2个填数,再右第2列中间1个填数,直到左第2列为止。在前面程序中,我们已经完成了前面部分,第(5)空所在的循环体就是用来完成后面部分的,在循环体中已经实现了对中、下进行填数,缺一个对上进行填数的代码,因此,第(5)空要完成的任务就是对上行进行填数,因此,答案为a[0][m-2*i-1]=k。 -
第3题:
按层次次序将一棵有n-个结点的完全二叉树的所有结点从1~n编号,当i≤n/2时,编号为i的结点的左子树的编号是( )。
A.2i-1
B.2i
C.2i+1
D.不确定
正确答案:B
B。【解析】完全二叉树中除最下面一层外,各层都被结点充满了,每一层结点个数恰是上一层结点个数的2倍。因此,从一个结点的编号就可推知它的双亲及左、右子树结点的编号。当i≤n/2时,编号为i的结点的左子树的编号是2i,否则结点i没有左子树。当i≤(n-1)/2时,编号为i的结点的右子树的编号是2i+1,否则结点i没有右子树。当i≠1时,编号为i的结点的双亲是结点i/2。 -
第4题:
有2007盏亮着的灯,各有一个拉线开关控制着,拉一下拉线开关灯会灭掉,再拉一下灯由灭变亮,现按其顺序将灯编号为1,2,…,2007,然后将编号为2的倍数的灯线都拉一下,再将编号为3的倍数的灯线都拉一下,最后将编号为5的倍数的灯线都拉一下,三次拉完后亮着的灯有多少盏?( )
 正确答案:D
正确答案:D
(如图所示)大方框1-2007表示这2007个灯,3个圆分别表示代表其中是2、3、5的倍数的灯的个数。圆中每个部分的数字表示被拉的次数,标有1和3的部分的灯是灭的,标有。和2的部分的灯是开的。2007个灯中编号为2的倍数的灯共1003盏(代表A的部分),编号为3的倍数的灯共669盏(代表字母8的部分),编号为5的倍数的灯共401盏(代表字母C的部分)。编号为6的倍数的灯共334盏;编号为10的倍数的灯共200盏;编号为15的倍数的灯共133盏;编号为30的倍数的灯共66盏。拉了3次的灯数为66盏(即能同时被2,3,5整除的数);拉了2次的灯数为334+200+133—3×66—469盏;拉了1次的灯数为1003+669+401-2×469-3×66=937盏。现在灭着的灯数为:937+66—1003(盏)。开着灯有2007-1003=1004(盏)。故选D。 -
第5题:
设有编号为1,2,3···,10的10张背面之上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1 的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,····,第n名(n≦10)游戏者,将所有编号是n的倍数的纸牌翻成另一面向上的状态,如此下去,当第10名游戏者翻完纸牌后,那些纸牌正面向上的最大编号与最小编号的差是:A. 2
B. 4
C. 6
D. 8答案:D解析:约数倍数计算类。逐个分析每个数字(1-10)的约数个数,10的约数有1、2、5、10,故10共被翻转四次,仍然背面向上;9的约数有1、3、9,共被翻转三次,正面向上。1的约数只有1,故向上。故正面向上的最大编号和最小编号分别为9、1,差值为8。因此,本题答案选择D选项。 -
第6题:
地上画有45 行、2 列的方格阵列,45 名运动员在靠左的一列站成纵队,每人站在一个方格内,且所有运动员从前到后按1~45 依次编号。当听到第一声哨响时,所有编号为1 的倍数的人移动到自己所在位置同一行的另外一个方格中,往后听到第n 次哨响时,所有编号为n 的倍数的人都要移动到自己所在位置同一行的另外一个方格中。那么哨响4 次之后,站在左边一列的人比站在右边一列的人:A.少5 人
B.少9 人
C.多5 人
D.多9 人答案:B解析:

方法二:题目所求为哨响4次,因此编号为1、2、3、4倍数的人发生了移动,1、2、3、4的公倍数为12,因此每12个人的移动是一样的,可以按12人为一周期进行分析。前12个人的移动情况见下表: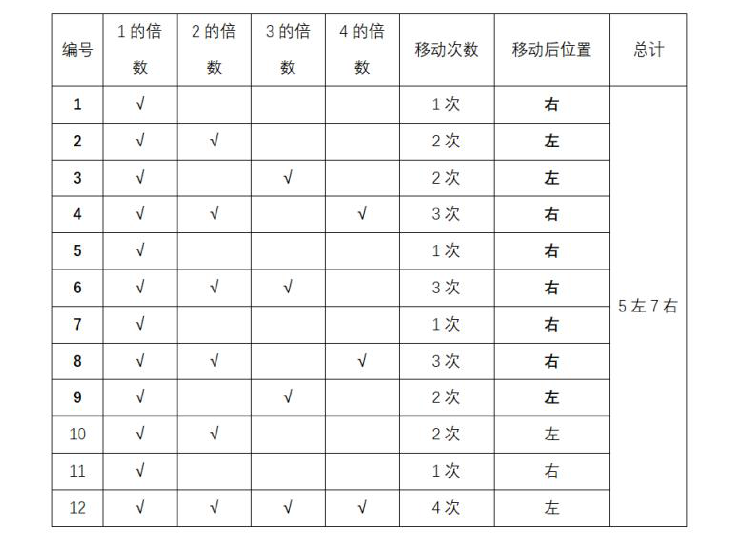

-
第7题:
设有编号为1到10的10张背面向上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,......,第n名(n≤10)游戏者,将所有编号是n的倍数的纸牌翻成另一面向上的状态,如此下去,当第10名游戏者翻完纸牌后,那些纸牌正面向上的最大编号与最小编号的差是:A. 2
B. 4
C. 6
D. 8答案:D解析:考虑各个正整数的因数的个数,只要因数的个数是奇数个,则该牌被翻动奇数次,显示的是正面;因数的个数是偶数个,则该牌被翻动偶数次,显示是背面。由于只有平方数的因数的个数是奇数个,其它数的因数的个数是偶数个,故最后显示正面的是编号是平方数的牌,即编号1、4、9这三张牌是显示正面,9-1=8,因此选D。 -
第8题:
韩国堪比中国的“斗地主的纸牌游戏是什么?
正确答案: 韩国堪比中国的“斗地主的纸牌游戏是花图。 -
第9题:
纸牌类桌面游戏“三国杀”是谁发明的()。
- A、中国人自主发明的
- B、韩国人自主发明的
- C、中国人根据美国游戏改编的
正确答案:C -
第10题:
有100个编号为1—100的罐子,第1个人在所有编号为1的倍数的罐子中倒入1毫升水,第2个人在所有编号为2的倍数的罐子中倒入1毫升水,……,第100个人在所有编号为100的倍数的罐子中倒入1毫升水,问此时第92号罐子中装了多少毫升的水?()
- A、2
- B、6
- C、46
- D、92
正确答案:B -
第11题:
判断题凯米等人将规则游戏分为瞄准游戏、赛跑游戏、追逐游戏、躲藏游戏、口令游戏、纸牌游戏、猜测游戏等八种类型。A对
B错
正确答案: 对解析: 暂无解析 -
第12题:
单选题设有编号为1、2、3……10的10张背面向上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号为2的倍数的纸牌翻成另一面向上的状态,……第n名(n≤10)游戏者,讲所有编号为n的倍数的纸牌翻成另一面向上的状态,如此下去,当第10名游戏者翻完纸牌后,那些纸牌正面向上的最大编号与最小编号的差是?( )A2
B4
C6
D8
正确答案: B解析: -
第13题:
按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号,当i≤n/2时,编号i的结点的左子女的编号是________。
A.2i-1
B.2i
C.2i+1
D.不确定
正确答案:B
解析:完全二叉树中除最下面一层外,各层都被结点充满了,每一层结点个数恰是上一层结点个数的2倍。因此,从一个结点的编号就可以推知它的双亲及左、右子女结点的编号。当i ≤ n/2时,结点i的左子女是结点2i,否则结点i没有左子女。当i ≤ (n-1)/2时,结点i的右子女是结点2i+1,否则结点i没有右子女。 -
第14题:
按层次次序将一棵有n个结点的完全二叉树的所有结点从1~n编号,当i≤n/2时,编号为i的结点的左子树的编号是( )。
A.2i-1
B.2i
C.2i+1
D.不确定
正确答案:B
完全二叉树中除最下面-层外,各层都被结点充满了,每-层结点个数恰是上-层结点个数的2倍。因此,从一个结点的编号就可推知它的双亲及左、右子树结点的编号。当i≤n/2时,编号为i的结点的左子树的编号是2i,否则结点i没有左子树。当i≤(n1)/2时.编号为i的结点的右子树的编号是2i+1,否则结点i没有右子树。当i≠1时,编号为i的结点的双亲是结点i/2。 -
第15题:
按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号,当i≤(n-1)/2时,编号i的结点的右子女的编号是( )。
A)2i-1
B)2i
C)2i 1
D)不确定
正确答案:C
-
第16题:
2006盏亮着的电灯,各有一个开关控制,按顺序编号为1,2,…,2006。将编号为2的倍数的灯的开关各按一下,再将编号为3的倍数的灯的开关各按一下,最后将编号为5的倍数的灯的开关各按一下。按完后亮着的灯有多少盏?( )A.1000
B.1002
C.1004
D.1006答案:C解析:因为灯在开始的时候是亮着的,所以按过两次或者没按过的灯最后还是亮的。本题实际上是求1到2006中不能被2、3、5整除的数和只能同时被2、3、5中两个数整除的数的总个数。能被2整除的有2006÷2=1003盏,能被3整除的数有2006÷3=668……2,共668盏,能被5整除的数有2006÷5=401……1,共401盏;其中,同时被2、3整除的数有2006÷(2x3)=334……2,共334盏,同时被3.5整除的数有2006÷(3x5)=133……11,共133盏,同时被2、5整除的数有2006÷(2×5)=200……6,共200盏,同时被2、3、5整除的数有2006÷(2×3×5)=66……26,共66盏,所以,只能同时被2、3、5中两个数整除的有334+133+200-3×66=469盏;不能被2、3、5整除的有2006-[(1003+668+401)-(334+133+200)+66]=535盏。故最后亮着的灯有469+535=1004盏。 -
第17题:
设有编号为1,2,3,……,10的10张背面向上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,……,第n名(n≤10)游戏者,将所有编号是n的倍数的纸牌翻成另一面向上的状态,如此下去,当第10名游戏者翻完纸牌后,那些纸牌正面向上的最大编号与最小编号的差是( )。A. 2
B. 3
C. 4
D. 5
E. 6
F. 7
G. 8
H. 9答案:G解析:枚举直到最后一次剩下1、4、9三个数,最大最小相差8. -
第18题:
设有编号为1、2、3.....10 的10张背面向上的纸牌,现有10名游戏者,第一名游戏者将所有编号时1的倍数的纸牌翻成另一面向上的状态,接着第二名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,.....,第n(n<=10)名游戏者,将所有编号是n的倍数的纸牌翻成另一面向上的状态,如此下去,当第10名游戏者翻完纸牌后,那些纸牌正面向上的最大编号和最小编号的差是:
A. 2
B. 4
C. 6
D. 8答案:D解析:约数倍数计算类。逐个分析每个数字(1-10)的约数个数,10的约数有1、2、5、10,故10共被翻转四次,仍然背面向上;9的约数有1、3、9,共被翻转三次,正面向上。1的约数只有1,故向上。故正面向上的最大编号和最小编号分别为9、1,差值为8。因此,本题答案选择D选项。 -
第19题:
2006盏亮着的电灯,各有一个开关控制,按顺序编号为1,2,…,2006。将编号为2的倍数的灯的开关各按一下,再将编号为3的倍数的灯的开关各按一下,最后将编号为5的倍数的灯的开关各按一下。按完后亮着的灯有多少盏?A.1000
B. 1002
C. 1004
D.1006答案:C解析:因为灯在开始的时候是亮着的,所以按过两次或者没按过的灯最后还是亮的。本题实际上是求1到2006中不能被2、3、5整除的数和只能同时被2、3、5中两个数整除的数的总个数。
能被2整除的有2006÷2=1003盏,
能被3整除的数有2006÷3=668……2,共668盏,
能被5整除的数有2006÷5=401……1,共401盏;
其中,同时被2、3整除的数有2006÷(2x3)=334……2,共334盏,
同时被3、5整除的数有2006÷(3×5)=133……11,共133盏,
同时被2、5整除的数有2006÷(2x5)=200……6,共200盏,
同时被2、3、5整除的数有2006÷(2x3x5)=66……26,共66盏,所以,只能同时被2、3、5中两个数整除的有334+133+200-3x66=469 盏;
不能被 2、3、5 整除的有2006-[( 1003+668+401 )-(334+133+200)+66]=535 盏。 故最后亮着的灯有469+535=1004盏。 -
第20题:
按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号,当i≤(n-1)/2时,结点i的右子女的结点编号为()。
正确答案:2i+1 -
第21题:
凯米等人将规则游戏分为瞄准游戏、赛跑游戏、追逐游戏、躲藏游戏、口令游戏、纸牌游戏、猜测游戏等八种类型。
正确答案:正确 -
第22题:
填空题按层次次序将一棵有n个结点的完全二叉树的所有结点从1到n编号,当i≤(n-1)/2时,结点i的右子女的结点编号为()。正确答案: 2i+1解析: 暂无解析 -
第23题:
单选题设有编号为1、2、3、…、10的10张背面向上的纸牌,现有10名游戏者,第1名游戏者将所有编号是1的倍数的纸牌翻成另一面向上的状态,接着第2名游戏者将所有编号是2的倍数的纸牌翻成另一面向上的状态,……,第n名(n≤10)游戏者,将所有编号是n的倍数的纸牌翻成另一面向上的状态,如此下去,当第10名游戏者翻完纸牌后,那些纸牌正面向上的最大编号与最小编号的差是:A2
B4
C6
D8
正确答案: B解析:
