下图中ABCD为边长10米的正方形路线,E为AD中点,F为与B相距3米的BC上一点,从E点到F点有小路EGHF,小路的每一段都与AB垂直或平行,且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒,则其以相同速度经EGHF从E点匀速运动到F点用时多少秒? A.12 B.10 C.9 D.8
题目
下图中ABCD为边长10米的正方形路线,E为AD中点,F为与B相距3米的BC上一点,从E点到F点有小路EGHF,小路的每一段都与AB垂直或平行,且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒,则其以相同速度经EGHF从E点匀速运动到F点用时多少秒?
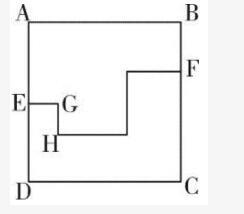

A.12
B.10
C.9
D.8
B.10
C.9
D.8
相似考题
更多“ 下图中ABCD为边长10米的正方形路线,E为AD中点,F为与B相距3米的BC上一点,从E点到F点有小路EGHF,小路的每一段都与AB垂直或平行,且GH相距2米。甲经EABF从E点匀速运动到F点用时9秒,则其以相同速度经EGHF从E点匀速运动到F点用时多少秒? ”相关问题
-
第1题:
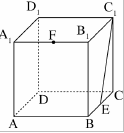
如右图所示,一个边长为10厘米的正方体木块ABCD-A1B1C1D1,点E、F分别是BC、A1B1的中点,C1E是用蜂蜜画的一条线段,一只蚂蚁在点F处,要想沿正方体表面最快到达蜂蜜所在线段C1E,它所爬行的最短距离是多少厘米?
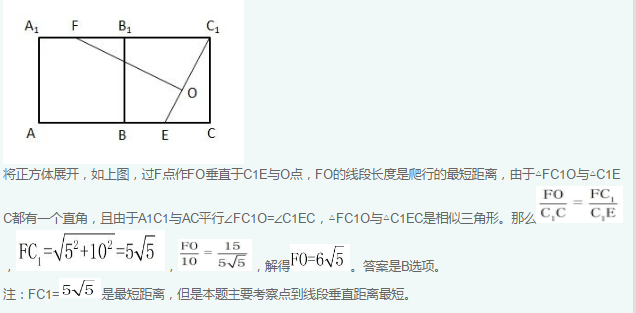
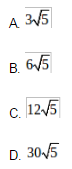 答案:B解析:知识点:体积计算
答案:B解析:知识点:体积计算
-
第2题:
(6分)如图,点P为矩形ABCD边BC上一点(不包括端点),E为BC延长线上一点,CQ为∠DCE的角平分线,连接AP,PQ,使AP⊥PQ。求证:当AB=BC时,存在AP=PQ。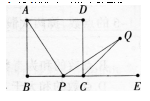 答案:解析:
答案:解析:
∴AP=PQ。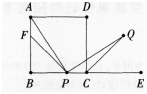
-
第3题:
如右图,在梯形ABCD中,点E、F分别是腰AB、CD上的点.
(1)证明:如果E、F为中点时,有 EF=1/2(AD+BC);
(2)请写出(1)中命题的逆命题,并判断该逆命题是否成立,若成立,请给予证明;若不成立,请说明理由.
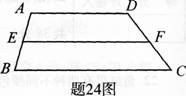 答案:解析:(1)证明:连接AC,设AC中点为日,连接EH、FH
答案:解析:(1)证明:连接AC,设AC中点为日,连接EH、FH

逆命题不成立.
理由如下:连接AC,连接BD,延长AD至M使DM=AD,延长BC至N,使CN=AD,连接MN、DN.由DM平行且等于CN可知,DN平行且等于AC由ADBN可知,BD+DM>BN,即BD+AC>BC+AD
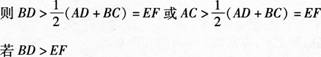
又AD<EF可知AD<EF<BD过点D作直线交AB于Q,则AD<DQ<BD,其中必有DQ=EF同理,若AC>EF,Q为DC上-点,则必有AQ=EF且A、D均不是AB、CD的中点故命题错误. -
第4题:
如右图,正方形的迷你轨道边长为1米,1号电子机器人从点A以1米/秒的速度顺时针绕轨道移动,2号电子机器人从点A以3米/秒的速度逆时针绕轨道移动,则它们的第2017次相遇在: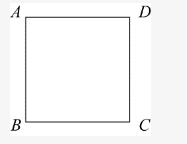 A.点A
A.点A
B.点C
C.点B
D.点D答案:D解析:第一步,本题考查行程问题,属于相遇追及类。
第二步,第1秒1号机器人顺时针走到点D,2号逆时针走到点D,故两个机器人每过1秒相遇一次,相遇点依次为D—C—B—A—D—C—B—A……每4次相遇为一个周期。
第三步,2017÷4=504…1,则第2017次相遇与第1次相遇地点是同一地点,即D点。 -
第5题:
如右图,两只小爬虫甲和乙从A点出发,沿长方形ABCD的边,按箭头方向爬行,在离C点32厘米的E点它们第一次相遇;在离D点16厘米的F点第二次相遇;在离A点16厘米的G点第三次相遇。求长方形的边AD长多少厘米? AB边长多少厘米?( )
A. 24 36 B. 48 54
C. 36 48 D. 48 64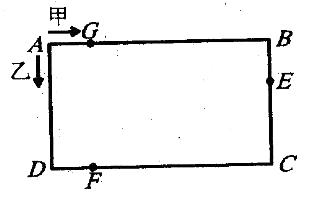 答案:D解析:设AD=BC=x厘米,AB = CD =y厘米,则乙虫第一次相遇时走了(x + y + 32)厘米,第一次相遇后到第二次相遇时又走了[(x - 32)+y +x+16]厘米。由于每次相遇时,两虫合起来走了一周,因此,两虫每次相遇时走的路程均相等。列方程得x+y+32= (x-32) +y+x+ 16,x= 48。
答案:D解析:设AD=BC=x厘米,AB = CD =y厘米,则乙虫第一次相遇时走了(x + y + 32)厘米,第一次相遇后到第二次相遇时又走了[(x - 32)+y +x+16]厘米。由于每次相遇时,两虫合起来走了一周,因此,两虫每次相遇时走的路程均相等。列方程得x+y+32= (x-32) +y+x+ 16,x= 48。
同理,甲虫第一次相遇时走了(y+x-32)厘米,第二次相遇到第三次相遇时走了(16 +x+16)厘米, 列方程得y+x-32 =16+x+16,y=64。
故长方形的边AB长64厘米,AD长48厘米,所以本题正确答案为D。 -
第6题:
如图所示,在长方形ABC.D中,AD=2AB,E为BC.的中点,F为EC.上任意一点(与E点、C.点不重合),从图形6个点中随机选取3个,能构成直角三角形的概率为:
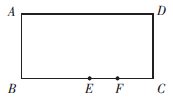 A.1/2
A.1/2
B.9/20
C.7/20
D.2/5答案:B解析:从6个点中随机选取3个,总共有

种选法。以A、B两点为准,任选E、F、C、D其中一点均可构成直角三角形。同理,以C、D两点为准,任选E、F、B、A其中一点均可构成直角三角形,总共有
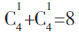
种。同时,因为E为BC中点,且AD=2AB,则△AED也是直角三角形,△AFD不是直角三角形,则所求为(8+1)/20=9。故本题选B。 -
第7题:
设y=f(x)可导,点a0=2为f(x)的极小值点,且f(2)=3,则曲线y=f(x)在点(2,3)处的切线方程为______.答案:解析:由于y=f(x)可导,点x0=2为f(x)的极小值点,由极值的必要条件可知f′(2)=0.曲线y=fx)在点(2,3)处的切线方程为y-3=f′(2)(x-2)=0,即y=3为所求切线方程. -
第8题:
如图,在一张矩形纸片ABCD中,AB=4,BC=8。点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点日处,点D落在G处,有以下四个结论:①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时, 。以上结论中,你认为正确的有( )个。 A.1
A.1
B.2
C.3
D.4答案:C解析:
-
第9题:
若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上的一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为5/2或12/5。
正确答案:错误 -
第10题:
设力F1,F2及点O都在某平面上,F1,F2不平行,其交点为A,且F1,F2对点O的力矩相等,下述说法正确的是()。
- A、对于过点O且垂直于此平面的直线上任一点B,必有MB(F1)=MB(F2)
- B、对于OA直线上的任一点B,必有MB(F1)=MB(F2)
- C、对过直线OA且与此平面垂直的平面上任一点B,必有MB(F1)=MB(F2)
- D、除O点外,不存在另一点B,使MB(F1)=MB(F2)
正确答案:B -
第11题:
单选题设AB两点间的距离为D,光线从A点发射至B点再反射回到A点所用时间为t,光速为c,则AB两点间的距离可按下式计算()。AD=2ct
BD=1/2ct
CD=1/4ct
DD=1/8ct
正确答案: C解析: 暂无解析 -
第12题:
单选题AC点到F点
BE点到F点
CB点到F点
DC点到D点
正确答案: B解析: -
第13题:
下列命题正确的是()A.函数f(x)的导数不存在的点,一定不是f(x)的极值点
B.若x0为函数f(x)的驻点,则x0必为f(x)的极值点
C.若函数f(x)在点x0处有极值,且f'(x0)存在,则必有f'(x0)=0
D.若函数f(x)在点x0处连续,则f'(x0)一定存在答案:C解析:根据函数在点x0处取极值的必要条件的定理,可知选项C是正确的. -
第14题:
如图。在直角梯形ABCD中,AB∥CD,∠BAD=90o,且AB=8,AD=3,CD=4,动点P,Q分别以点B和点A为起点同时出发,点P沿B→A,以每秒1个单位速度运动,终点为点A;点Q沿A→D→C→B,以每秒1.5个单位速度运动,终点为点B。设△APQ的面积为y,运动时间为x。
(1)求y关于x的函数解析式y=f(x);
(2)画出函数y=f(x)的图象。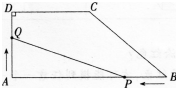 答案:解析:
答案:解析:
(2)函数图象如图所示: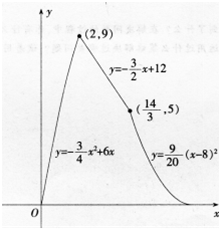
-
第15题:
如图,边长为a的正方形ABCD中,点E是对角线BD上的一点,且BE=BC,点P在EC上,PM⊥BD于M,PN⊥BC于N,则PM+PN=________。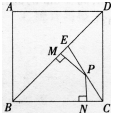 答案:解析:
答案:解析: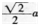
解析:作EK⊥BC于K,连接BP,由△EBC的面积等于△PBE和△PBC的面积之和且BE=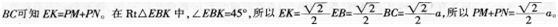
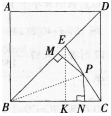
-
第16题:
平行四边形ABCD如右图所示,E为AB上的一点,F、G分别是AC和DE、DB的交点。若AB=3AE,则四边形BEFG与ABCD的面积之比是:A.2︰7
B.3︰13
C.4︰19
D.5︰24答案:D解析:第一步,本题考查几何问题,属于平面几何类,用赋值法解题。
第二步,题干没给出具体数值,可以采用赋值法解题。赋值AB=3,平行四边形ABCD的高为4,则AE=1;由于△AEF相似于△CDF,则两个三角形的高之比为AE:DC=1︰3,可知△AEF的高为
4*1/4=1。△ABG与△CDG全等,则△ABG的高为4÷2=2。
第三步,四边形BEFG面积=△ABG面积-△AEF面积=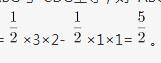
四边形ABCD面积=3×4=12,两者之比为 ︰12=5︰24。
因此,选择D选项。 -
第17题:
如图所示,有一束平行于等边三棱镜截面ABC的单色光从空气射向E点,并偏折到F点。已知入射方向与边AB的夹角为θ=30。,E、F分别为边AB、BC的中点,则( )。

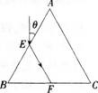 答案:C解析:
答案:C解析: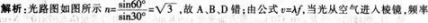
不变,光速变小,波长变小,故选C。

-
第18题:
如图,平行四边形ABCD的面积是54平方厘米,点E、F、G分别是平行四边形ABCD边上的中点,H为AD边上的任意一点,则阴影部分的面积为( )平方厘米。
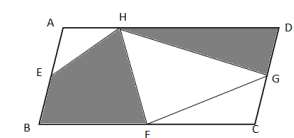 A. 27
A. 27
B. 28
C. 32
D. 36答案:A解析:方法一:如图所示,由于H为AD边上的任意一点,假设H点与A点重叠,则左边阴影为三角形ABF,其面积为三角形ABC的一半;右边阴影为三角形ADG,其面积为三角形ACD的一半。因此题目所求为平行四边形ABCD面积的一半,平行四边形ABCD的面积是54平方厘米,则阴影部分面积为27平方厘米。因此,本题答案为A选项。
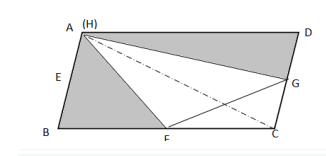
方法二:如图所示,连接BH和CH,由于点E、F、G分别是平行四边形ABCD边上的中点,则三角形AEH和BEH相等,三角形BFH和CFH相等,三角形CGH和DGH相等,因此题目所求的阴影部分为平行四边形ABCD的一半。平行四边形ABCD的面积是54平方厘米,则阴影部分面积为27平方厘米。因此,本题答案为A选项。
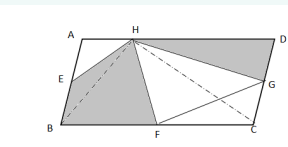
-
第19题:
下列命题中正确的为()A.若xo为f(x)的极值点,则必有,f'(xo)=0
B.若f'(xo)=0,则点xo必为f(x)的极值点
C.若f'(xo)≠0,则点xo必定不为f(x)的极值点
D.若f(x)在点xo处可导,且点xo为f(x)的极值点,则必有f'(xo)=0答案:D解析:由极值的必要条件知D正确.Y=|x|在x=0处取得极值,但不可导,知A与C不正确.y=x3在xo=0处导数为0,但Xo=0不为它的极值点,可知B不正确.因此选D. -
第20题:
在寻求两点最短路径问题解决方法中,O为起始点,与E,F,G点相连,距离为3,4,5,则可以得出已解点为()
- A、E点
- B、F点
- C、G点
- D、O点和E点
正确答案:D -
第21题:
质点沿直线以O为平衡位置做简谐运动,A、B两点分别为正最大位移处与负最大位移处的点,A、B相距10cm,质点从A到B的时间为0.1s,从质点到O点时开始计时,经0.5s,则下述说法正确的是()
- A、振幅为5cm
- B、振幅为10cm
- C、通过路程50cm
- D、质点位移为50cm
正确答案:A,C -
第22题:
润滑油“三过滤”的正确顺序为()。
- A、从领油大桶到岗位储油桶-从岗位储油桶到油壶-从油壶到加油点
- B、从岗位储油桶到油壶-从油壶到领油大桶-从领油大桶到加油点
- C、从领油大桶到岗位储油桶-从岗位储油桶到加油点-从加油点到油桶
- D、从岗位储油桶到油壶-从油壶到加油点-从加油点到领油大桶
正确答案:A -
第23题:
判断题若正方形ABCD的边长为4,E为BC边上一点,BE=3,M为线段AE上的一点,射线BM交正方形的一边于点F,且BF=AE,则BM的长为5/2或12/5。A对
B错
正确答案: 错解析: 暂无解析
