在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球? A. 14 B. 15 C. 17 D. 18

题目
在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球?

A. 14
B. 15
C. 17
D. 18
相似考题

1.袋中有球12个,2白10黑,今从中取4个,试求(1)恰有一个白球的概率(2)至少有一个白球的概率。

2.在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球？A．14 B．15 C．17 D．18

3.一个袋内有100个球，其中有红球28个、绿球20个、黄球12个、蓝球20个、白球10个、黑球10个。现在从袋中任意摸球出来，如果要使摸出的球中，至少有15个球的颜色相同，问至少要摸出几个球才能保证满足上述要求?（ ）A．78B．77C．75D．68

4.三个箱子,第一个箱子中有4个黑球2个白球,第二个箱子中有3个黑球5个白球,第三个箱子中有3个黑球2个白球。试求:随机地取一个箱子,再从这个箱子中任取出一球,这个球为白球的概率是多少?

更多“在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球? ”相关问题

  • 第1题：

    （3）一个口袋内装有除颜色外其他都相同的6个白球和4个红球，从中任意摸出2个，求：A、2个都是白球的概率；B、2个都是红球的概率；C、一个白球，一个红球的概率。


    正确答案：
              

  • 第2题：

    一个袋内有l00个球，其中有红球28个、绿球20个、黄球12个、蓝球20个、白球10、黑球10个。现在从袋中任意摸球出来，如果要使摸出的球中，至少有15个球的颜色相同，问至少要摸出几个球才能保证满足上述要求?（ ）

    A．78个

    B．77个 >>>>>

    C．75个

    D．68个


    正确答案：C
    最坏情况：摸出14个红球、14个绿球、12个黄球、14个蓝球、10个白球、10个黑球；则还需要从剩下的球中摸出1个球才能满足要求。即至少要摸出14×3+12+10+10+1=75个球才能满足题目要求。故选C。

  • 第3题：

    一袋中有5个乒乓球，其中4个白球，1个红球，从中任取2个球的不可能事件是（）

    A.｛2个球都是白球｝
    B.｛2个球都是红球｝
    C.｛2个球中至少有1个白球｝
    D.｛2个球中至少有1个红球｝

    答案：B
    解析：
    袋中只有1个红球，从中任取2个球都是红球是不可能发生的．

  • 第4题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的 2/7；若取出两个白球，则袋中白球占 2/3。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第5题：

    一个口袋中有4个白球，1个红球，7个黄球．搅匀后随机从袋中摸出1个是白球的概率是_________．


    答案：
    解析：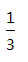

  • 第6题：

    在一个口袋里有黑球、白球、红球、蓝球各13个，则至少取出几个球才能保证有6个相同颜色的球（）

    • A、24
    • B、23
    • C、22
    • D、21

    正确答案:D

  • 第7题：

    单选题
    在一个口袋中有10个黑球、6个白球、4个红球．问：至少从中取出多少个球，才能保证其中有白球？
    A

    14

    B

    15

    C

    17

    D

    18


    正确答案： B
    解析：

  • 第8题：

    单选题
    在一个口袋里有黑球、白球、红球、蓝球各13个，则至少取出几个球才能保证有6个相同颜色的球（）
    A

    24

    B

    23

    C

    22

    D

    21


    正确答案： D
    解析： 根据最差原则，先取出黑球、白球、红球、蓝球各5个，最后任意取出1个球，都能保证有6个颜色相同的球。5×4+1=21。

  • 第9题：

    在一个口袋中有10个黑球、6个白球、4个红球，至少从中取出多少个球才能保证其中有白球?

    A．14

    B．15

    C．17

    D．18


    正确答案：B
    [答案] B。解析：抽屉原理，最坏的情况是10个黑球和4个红球都拿出来了，第15次拿到的肯定是白球。

  • 第10题：

    某袋内有70个球，其中20个是红球，20个是绿球，20个是黄球，其余是黑球和白球。为确保取出的球中至少包含有10个同色的球，问最少必须从中取出几个球？（ ）

    A. 28
    B. 38
    C. 18
    D. 52

    答案：B
    解析：
    根据题意，黑球和白球个数之和是(70-20X3) = 10(个)。所以同色的10个球只能是红色、绿色或黄色中的一种。假设袋子中只有红球、绿球和黄球三种球，把这三种颜色看做三只抽屉，每只抽屉中放9个球，就要取出9X3 = 27(个)球，如果再多取一个球，就能保证至少有一只抽屉内有10个球，也就是至少有10个同色的球。因为袋中还有10个黑球和白球，取出球的个数只要再加10个，才能保证含有10个同色球。
    9X3 +1+ (70-20X3) = 27 + 1 + 10 = 38(个)
    最少必须从袋子中取出38个球。故本题选B。

  • 第11题：

    一个口袋内有4个不同的红球，6个不同的白球.
    (1)从中任取4个球，红球的个数不比白球少的取法有多少种?
    (2)若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种?


    答案：
    解析：
    解：(1)由题意知本题是一个分类计数问题.将取出4个球分成三类情况：取4个红

  • 第12题：

    袋子中有若干黑球和白球。若取出一个黑球，则袋中黑球占总球数的



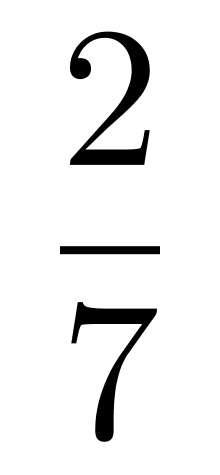
    ；若取出两个白球，则袋中白球占



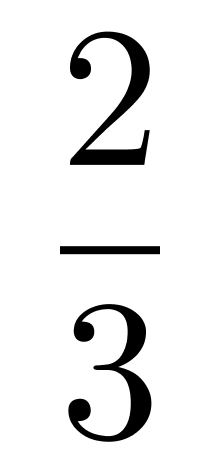
    。从原来袋中抽出3个球，其中有且仅有1个黑球的概率：

    A.低于20%
    B.在20%—40%之间
    C.在40%—60%之间
    D.高于60%

    答案：C
    解析：
    第一步，本题考查概率问题，用方程法解题。

  • 第13题：

    已知一个口袋里有5个红球，6个白球，7个黑球，则至少取出多少个球才能保证有一个红球和一个白球？（）

    • A、3个
    • B、9个
    • C、13个
    • D、14个

    正确答案:D

  • 第14题：

    单选题
    一个盒子里有20个球，其中有18个红球，2个黑球，每个球除颜色外都相同，从中任意取出3个球，则下列结论中，正确的是(　　)
    A

    所取出的3个球中，至少有一个是黑球 

    B

    所取出的3个球中，至少有2个黑球

    C

    所取出的3个球中，至少有1个是红球  

    D

    所取出的3个球中，至少有2个是红球


    正确答案： A
    解析： 暂无解析

  • 第15题：

    单选题
    一个袋内有100个球，其中有红球28个、绿球20个、黄球12个、蓝球20个、白球10个、黑球10个。现在从袋中任意摸球出来，如果要使摸出的球中，至少有15个球的颜色相同，问至少要摸出几个球才能保证满足上述要求？（　　）
    A

    78个

    B

    77个

    C

    75个

    D

    68个


    正确答案： B
    解析：
    设手中有100个球，尽量不发出15个颜色相同的球。先将每种颜色的球发出14个，不足14个的全部发出，则共计发出14＋14＋12＋14＋10＋10＝74个，但剩下的球中任意再发出1个就满足要求了。因此至少要摸出75个球。

  • 第16题：

    单选题
    已知一个口袋里有5个红球，6个白球，7个黑球，则至少取出多少个球才能保证有一个红球和一个白球？（）
    A

    3个

    B

    9个

    C

    13个

    D

    14个


    正确答案： D
    解析： 暂无解析

相关内容