10个相同的盒子中分别装有1—10个球,任意两个盒子中的球数都不相同,小李分三次,每次取出若干个盒子,每次取出的盒子中的球数之和都是上一次的3倍,且最后剩下一个盒子。剩下的盒子中有多少个球?A.9 B.6 C.5 D.3
题目
B.6
C.5
D.3
相似考题
更多“10个相同的盒子中分别装有1—10个球,任意两个盒子中的球数都不相同,小李分三次,每次取出若干个盒子,每次取出的盒子中的球数之和都是上一次的3倍,且最后剩下一个盒子。剩下的盒子中有多少个球?”相关问题
-
第1题:
盒子中装有很多相同的,但分红、黄、蓝三种颜色的玻璃球,每次摸出两个球,为了保证有5次摸出的结果相同,则至少需要摸球( )次。 A.20 B.21 C.24 D.25
正确答案:D
每次摸出两个球,共有6种情况,分别是:红红、黄黄、蓝蓝、红黄、红蓝、黄蓝。考虑最差可能,即每种情况都摸出4次,则只需再摸1次,就可保证5次摸出的结果相同,所求为4x6+1=25次。
-
第2题:
将12个球放入3个盒子里,使每个盒子里球的数目是偶数,且没有空盒,问共有几种放法?( )
A.10
B.12
C.8
D.6
正确答案:A
设三个盒子所放的球的数量为(x,y,z),则有(2,2,8),(2,4,6),(2,6,4),(2,8,2),(4,2,6),(4,4,4),(4,6,2),(6,2,4),(6,4,2),(8,2,2)。共10种。本题选A。 -
第3题:
A、B、C、D四个盒子中依次放有6、4、5、3个球。第l个小朋友找到放球最少的盒子,从其他盒子中各取一个球放入这个盒子;然后第2个小朋友找到放球最少的盒子,从其他盒子中各取一个球放入这个盒子……如此进行下去。当34位小朋友放完后,问B盒子中放有多少个球?( )
A.4
B.6
C.8
D.11
正确答案:B -
第4题:
现在将编号为1、2、3、4、5、6的6个球分别放入编号为1、2、3、4、5、6的6个盒子里,每个盒子放1个球。请问,恰好有2个盒子编号与球编号一样的投放方法有多少种?
A.15
B.24
C.135
D.270
正确答案:C
首先选出2个编号和球一样的盒子,有C62=15种方法;剩余的4个再进行错位重排,有3×3=9种方法。因此一共有15×9=135种方法。
-
第5题:
有三只盒子,每只盒子里面装了两只球,分别是黑黑,白白,黑白。每只盒子都贴上了标明内容的标签,但所有的标签都贴错了。要求:打开一只盒子,但只能去除一个球来,看过之后吧所有的标签都纠正过来。可以打开的盒子是()A. 黑黑
B. 白白
C. 黑白
D. 打开哪个盒子都不行答案:C解析:运用假设法。假设打开写有“黑白”标签的盒子,那么该盒子只可能是装有“黑黑”或“白白”,如果取出一个黑球,则该盒子是“黑黑”,则写有白白的盒子,一定是“黑白”,可知写有“黑黑”的盒子是“白白”,同理,如果摸出的是白球,一样鞥确定所有标签。而假设打开写有“黑黑”的盒子,这个盒子里应该装的是“黑白”或者“白白”则如果摸出的是白球,就无法确定这个盒子里装的是什么,同样打开写有“白白”的盒子,也不一定可以确定。故答案为C。 -
第6题:
一个盒子里有乒乓球100多个,如果每次取5个出来最后剩下4个,如果每次取4个最后剩3个,如果每次取3个最后剩2个,那么如果每次取12个最后剩多少个?( )A.11
B.10
C.9
D.8答案:A解析:第一步,本题考查余数问题,用余数定理解题。
第二步,考查余数问题,根据余数定理,差同减差(如果每次取5个出来最后剩下4个,5-4=1;如果每次取4个最后剩3个,4-3=1;,如果每次取3个最后剩2个,3-2=1),最小公倍数做周期,故总数为60n-1,当n=2时,满足总数为119。
第三步,每次取12个,119÷12=9...11。 -
第7题:
三个相同的盒子里各有2个球,其中一个盒子里放了2个红球,一个盒子里放了2个蓝球,一个盒子里放了红球和蓝球各1个。随机选择一个盒子后从中随机摸出一球是红球,则这个盒子里另一个球是红球的概率为( )。A.1/2
B.3/4
C.2/3
D.4/5答案:C解析:
-
第8题:
设有编号为1,2,3,4,5的5个球和编号为1,2,3,4,5的5个盒子,将5个小球放入5个盒子中(每个盒子中放入1个小球),则至少有2个小球和盒子编号相同的方法有( )A.36种
B.49种
C.31种
D.28种
E.72种答案:C解析:
-
第9题:
要把85个球放人若干个盒子中,每个盒子中最多放7个。问:至少有几个盒子中的球的数目相同?()
A. 2 B. 3 C. 4 D. 5答案:C解析:每盒放1,2,3,4,5,6,7个球,这样的七盒共放球:
1+2 + 3+4+5 + 6 + 7 = 28(个),85/28 = 3... 1。
所以至少有4个盒中的球数相同。故本题正确答案为C。 -
第10题:
两个盒子里都有糖果,一个盒子里的糖果数是奇数,另一个盒子里的糖果数是偶数。如果右边盒子里的糖果数乘3,左边盒子里的糖果数乘2,然后把两个数加起来,和是49。猜一猜哪个盒子里的糖果数是奇数()
- A、左边
- B、右边
- C、左右边都是
- D、无法确定
正确答案:B -
第11题:
单选题一个盒子里有20个球,其中有18个红球,2个黑球,每个球除颜色外都相同,从中任意取出3个球,则下列结论中,正确的是( )A所取出的3个球中,至少有一个是黑球
B所取出的3个球中,至少有2个黑球
C所取出的3个球中,至少有1个是红球
D所取出的3个球中,至少有2个是红球
正确答案: A解析: 暂无解析 -
第12题:
单选题将20个相同的小球放入编号分别为1,2,3,4的四个盒子中,要求每个盒子中的球数不少于它的编号数,则共有多少种放法?A340
B286
C446
D364
正确答案: A解析: -
第13题:
现在将编号为1、2、3、4、5、6的6个球分别放入编号为1、2、3、4、5、6的6个盒子里,每个盒子放1个球。请问。恰好有2个盒子编号与球编号一样的投放方法有多少种? A.15 B.24 C.135 D.270
正确答案:C
首先选出2个编号和球一样的盒子, 剩余的4个再进行错位重排,有3x3=9种方法。因此一共有15×9=135种方法。
剩余的4个再进行错位重排,有3x3=9种方法。因此一共有15×9=135种方法。
-
第14题:
将四个颜色互不相同的球全部放人编号为1和2的两个盒子里,使得放入每个盒子里球的个数不小于盒子的编号,则不同的放球方法有( )种。 A.9 B.10 C.12 D.18
正确答案:B
-
第15题:
将四个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里球的个数不小于盒子的编号,则不同的放球方法有( )种。
A.9
B.10
C.12
D.18
正确答案:B
-
第16题:
有红、黄、白三种颜色的球各4个,放在一个盒子里,至少取出()个球,可以保证取到4个颜色相同的球
A.8
B.9
C.10
D.11
正确答案:C
-
第17题:
黑白两个盒子中共有棋子193颗。若从白盒子中取出15颗棋子放入黑盒子中,则黑盒子中的棋子数是白盒子中棋子数的m(m为正整数)倍还多6颗。那么,黑盒子中原来的棋子至少有( )A.121颗 B.140颗 C.161颗 D.167颗答案:C解析:由题意可以得出,193-6=187=11×17,根据11、17均为质数这一特性,要使得黑盒子中的棋子数最少,令白盒子中的棋子数最大=17,则放入后黑盒子中的棋子数=193-17=176,放入前黑盒子中的棋子数=176-15=161。 -
第18题:
有三个盒子,第一个盒子有4个红球1个黑球,第二个盒子有3个红球2个黑球,第三个盒子有2个红球3个黑球,如果任取一个盒子,从中任取3个球,以X表示红球个数.
(1)写出X的分布律;(2)求所取到的红球数不少于2个的概率.答案:解析: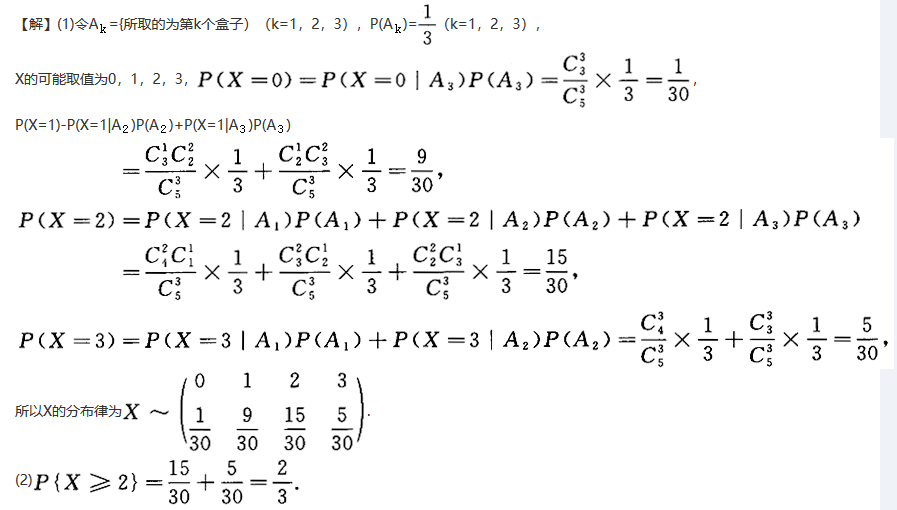
-
第19题:
若将15只相同的球随机放入编号为1,2,3,4的四个盒子中,1号盒可以为空,其余盒子中小球数目不小于盒子编号,则不同的投放方法有( )种A.56
B.84
C.96
D.108
E.120答案:B解析:
-
第20题:
若将15只相同的球随机放入编号为1,2,3,4的四个盒子中,每个盒子中小球的数目,不少于盒子的编号,则不同的投放方法有( )种A.56
B.84
C.96
D.108
E.120答案:A解析:减少元素法,第一步:先将1,2,3,4四个盒子分别放0,1,2、3个球,因为球是相同的球,故只有一种放法.第二步:余下的9个球放入四个盒子、则毎个盒子至少放一个,使用挡法,即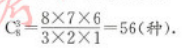
-
第21题:
盒子里有同样数目的黑球和白球。每次取出8个黑球和5个白球,取出几次后,黑球没有了,白球还剩12个。则共取了()次。
- A、3
- B、4
- C、5
- D、6
正确答案:B -
第22题:
1000个红球,1000个白球,放入两个盒子中,每个盒子放1000个球,有()种放法。
正确答案:1001种 -
第23题:
单选题两个盒子里都有糖果,一个盒子里的糖果数是奇数,另一个盒子里的糖果数是偶数。如果右边盒子里的糖果数乘3,左边盒子里的糖果数乘2,然后把两个数加起来,和是49。猜一猜哪个盒子里的糖果数是奇数()A左边
B右边
C左右边都是
D无法确定
正确答案: B解析: 依题意有3×右+2×左=49,根据奇偶性知道3×右为奇数,故右为奇数。
