如图，圆锥高厘米，底面半径为6厘米，一只蚂蚁从A.点沿圆锥侧面爬行到B.点，则最短的距离为_________厘米。A.12 B. C.6π D.24

题目
如图，圆锥高厘米，底面半径为6厘米，一只蚂蚁从A.点沿圆锥侧面爬行到B.点，则最短的距离为_________厘米。



A.12
B.
C.6π
D.24
相似考题

1.圆锥的底面半径为8，母线长为9，则该圆锥的侧面积为（ ）．（A）36л （B）48л （C）72л （D）144л

2.一个长方形铁锭，底面周长为32厘米，长与宽的比是3︰1，高比宽短30%。用它刚好可以铸成高为6厘米的圆锥体，那么圆锥体的底面积为（ ）平方厘米。A．67.2B．201.6C．537.6D．1612.8

3.一圆锥的侧面积恰好等于其底面积的2倍，则该圆锥侧面展开图所对应扇形圆心角的度数为_________。

4.下列关于圆锥及投影作图方法说法有误的一项是()A.圆锥底面为水平圆时，其正面投影和侧面投影积聚为正平线B.绘制圆锥投影时，通常最后画出圆锥在各投影位置上的对称中心线C.圆锥的轴线垂直于水平面时，圆锥底面为水平圆D.圆锥是由底面和圆锥面组成的

参考答案和解析
答案：B
解析：

更多“如图，圆锥高厘米，底面半径为6厘米，一只蚂蚁从A.点沿圆锥侧面爬行到B.点，则最短的距离为_________厘米。 ”相关问题

  • 第1题：

    一个底面直径为12厘米，高为18厘米的圆锥体铁块，完全浸没在一个装满水的底面半径为12厘米的圆柱形玻璃杯中，当铁块取出后，杯中水的液面会下降( )厘米。

    A．1

    B．1.5

    C．6

    D．4.25

  • 第2题：

    锥度是指()

    A.锥高与正圆锥的底面半径之比

    B.正圆锥的底圆直径与锥高之比

    C.正圆锥锥顶的角度

    D.锥体的斜度


    正确答案：B

  • 第3题：

    一个圆锥的侧面展开图是半径为8 cm，圆心角120°的扇形，则此圆锥底面半径是( )。



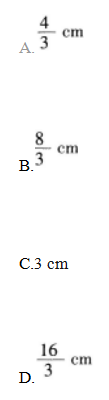    答案：B
    解析：
    由圆锥侧面展开图的半径和圆心角可得出扇形的弧长，扇形的弧长则为底面圆的周长，

  • 第4题：

    一个底面积为9平方厘米的圆锥和一个棱长为3厘米的正方体的体积相等，圆锥的高是( )。

    A.3厘米
    B.6厘米
    C.9厘米
    D.18厘米

    答案：C
    解析：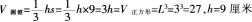

  • 第5题：

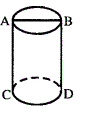    正圆柱体的高为10cm，底面半径为那么，在圆柱体的表面，从A点到D点的最短距离为（ ）。


    答案：B
    解析：
    沿AC这条线把圓柱剪开，由题意可得，其展开图的矩形的宽为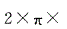，长为10cm，D为其一边长的中点，故从A点到D点的最短距离为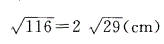故选 B。

  • 第6题：

    已知正圆锥的底面半径是1cm，母线为3cm，P为底面圆周上一点，由P绕过圆锥回到P点的最短路径如图所示，由顶点V到这条路线的最小距离是多少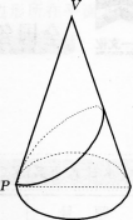


    答案：
    解析：
    圆锥的曲面沿着母线剪开，展开成一个平面(如下图)，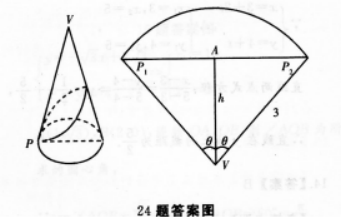

    其半径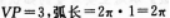的扇形
    短距离，就是弦PlP2，由V到这条路线的最短距离是图中的线段h=AV．依据弧长公式2π=2θ·3，得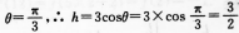

  • 第7题：

    一只蚂蚁位于2×2×2正方体空心框架的A点，向B点爬行。如果只准沿着框架线条爬。则最短路线一共有几条?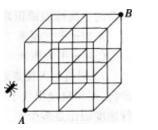

    A.64
    B.90
    C.99
    D.100

    答案：B
    解析：
    要求最短路径，则蚂蚁在每个点只能向上、前、右爬。记向右爬为x，向前爬为y，向上爬为

  • 第8题：

    五根半径不同的钢管从细到粗彼此相切地摆在地面上，上面放一块木板与每根钢管都相切，若最细钢管半径为8厘米，最粗钢管半径为18厘米，则最中间的钢管直径为：

    A.10厘米
    B.12厘米
    C.20厘米
    D.24厘米

    答案：D
    解析：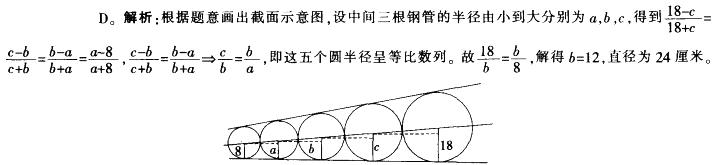

  • 第9题：

    圆锥的底面半径为4，母线长为5，那么它的侧面积是__________。


    答案：
    解析：

  • 第10题：

    一个圆锥形的积木，已知其底面积为0.3平方厘米，高为1厘米，则其体积为（）立方厘米。

    • A、0.3
    • B、0.2
    • C、0.15
    • D、0.1

    正确答案:D

  • 第11题：

    若圆柱的底面半径为5cm，高为4cm，则圆柱的侧面积为（）平方厘米。


    正确答案:40π

  • 第12题：

    填空题
    若圆柱的底面半径为5cm，高为4cm，则圆柱的侧面积为（）平方厘米。

    正确答案： 40π
    解析： 暂无解析

  • 第13题：

    一个盛有水的圆柱形容器，底面内半径为5厘米，深20厘米，水深15厘米。今将一个底面半径为2厘米，高为17厘米的实心铁圆柱垂直放入容器中。求这时容器的水深是多少厘米?( )

    A. 17.72              B. 16.64              C. 15              D. 22.6


    A【解析】若圆柱体能完全浸入水中，则水深与容器底面面积的乘积应等于原有水的体积与圆柱体在水中体积之和，因而水深为
    　　=17.72(厘米)
    　　它比圆柱体的高度要大，可见圆柱体可以完全浸入水中。
    于是所求的水深便是17.72厘米

  • 第14题：

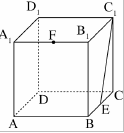
    如右图所示，一个边长为10厘米的正方体木块ABCD-A1B1C1D1，点E、F分别是BC、A1B1的中点，C1E是用蜂蜜画的一条线段，一只蚂蚁在点F处，要想沿正方体表面最快到达蜂蜜所在线段C1E，它所爬行的最短距离是多少厘米？




    答案：B
    解析：
    知识点:体积计算

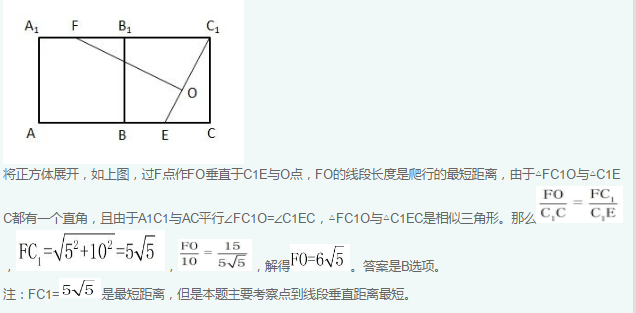
  • 第15题：

    在平面内，一只蚂蚁从点O出发，按向上、向右、向下、向右的方向依次不断移动．每次移动一个单位，其行走路线如图，则蚂蚁从点A2016到A2018的移动方向是( )。




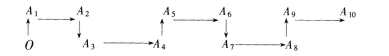
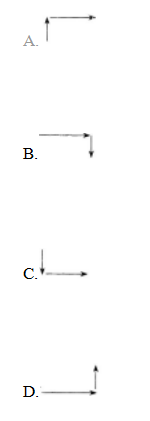    答案：A
    解析：
    蚂蚁爬行时移动的改变方向是循环O→A1→A2→A3→A4路线，所以A2016→A2017→A2018与O→A1→A2的路线相同。

  • 第16题：

    一个伞状玩具有一竖直柄，转动时柄顶端固定的一圈吊绳以柄顶端为顶点转动，形成一个圆锥体，且圆锥体底面刚好与柄底端位于一个平面上。已知绳长10厘米，柄长8厘米，则此玩具转动时所需空间最小应为（ ）立方厘米。

    A. 24π
    B. 120π
    C. 96π
    D. 288π

    答案：C
    解析：
    由题可知，只需算出圆锥体的体积即可。
    圆锥体即是一个直角三角形以一条直角边为轴旋转一周经过的空间。结合题干可知，绳长与柄长分别是形成圆锥体的直角三角形的斜边和一个直角边，根据勾股定理，形成圆锥体底面的直角边长为(厘米），因此，圆锥体的底面积为

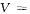
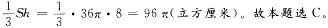
  • 第17题：

    如右图，两只小爬虫甲和乙从A点出发，沿长方形ABCD的边，按箭头方向爬行，在离C点32厘米的E点它们第一次相遇；在离D点16厘米的F点第二次相遇；在离A点16厘米的G点第三次相遇。求长方形的边AD长多少厘米？ AB边长多少厘米？（ ）
    A. 24 36 B. 48 54
    C. 36 48 D. 48 64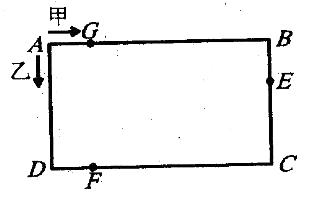


    答案：D
    解析：
    设AD=BC=x厘米，AB = CD =y厘米，则乙虫第一次相遇时走了(x + y + 32)厘米，第一次相遇后到第二次相遇时又走了[(x - 32)+y +x+16]厘米。由于每次相遇时，两虫合起来走了一周，因此，两虫每次相遇时走的路程均相等。列方程得x+y+32= (x-32) +y+x+ 16，x= 48。
    同理，甲虫第一次相遇时走了(y+x-32)厘米，第二次相遇到第三次相遇时走了(16 +x+16)厘米， 列方程得y+x-32 =16+x+16，y=64。
    故长方形的边AB长64厘米，AD长48厘米，所以本题正确答案为D。

  • 第18题：

    如图6-28所示,有一圆柱,高h=3厘米,底面半径r=3厘米,在圆柱下底面的点A处有一只蚂蚁,沿圆柱表面爬行到同一纵切面的斜上方的B点,则蚂蚁沿表面爬行时最短路程是（ ）.（π≈3）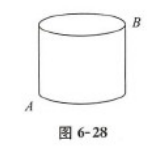



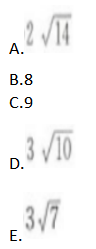    答案：C
    解析：

  • 第19题：

    有一只底面半径是20厘米的圆柱形水桶，里面有一段半径是5厘米的圆柱体钢材浸在水中。钢材从水桶里取出后，桶里的水下降了6厘米。这段钢材有多长？（ ）
    A. 12厘米 B. 24厘米 C. 72厘米 D. 96厘米


    答案：D
    解析：
    根据題意可知，圆柱形钢材的体积等于桶里下降部分水的体积，因为钢材底面半径是水桶底面半径的5/20，即1/4，钢材底面积就是水桶底面积的1/16。根据体积一定，圆柱体的底面积与高成反比例可知，钢材的长是水面下降高度的16倍。
    解法一:6/(5/20)2=96(厘米)。
    解法二:3. 14X202 X6/(3. 14X 52) = 96(厘米)。
    故本题正确答案为D。

  • 第20题：

    —个伞状玩具有一竖直柄，转动时柄顶端固定的一圈吊绳以柄顶端为顶点转动，形成一个 圆锥体，且圆锥体底面刚好与柄底端位于一个平面上。已知绳长10厘米，柄长8厘米，则 此玩具转动时所需空间最小应为（ ）立方厘米。

    A. 24π B. 1207π C. 96π D. 288π


    答案：C
    解析：
    C [解析]由题可知，只需算出圆锥体的体积即可，圆锥体即是一个直角三角形以

  • 第21题：

    已知点沿半径为40cm的圆周运动，其运动规律为s=20t（s以厘米计，t以秒计）。 若t=ls，则点的速度与加速度的大小为（ ）。


    答案：B
    解析：
    提示：点的速度、切向加速度和法向加速度分别为：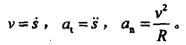

  • 第22题：

    一个圆柱和一个圆锥的底面积和体积分别相等，如果圆锥的高是9厘米，圆柱的高是（）

    • A、3厘米
    • B、9厘米
    • C、27厘米

    正确答案:A

  • 第23题：

    单选题
    一个圆柱和一个圆锥的底面积和体积分别相等，如果圆锥的高是9厘米，圆柱的高是（）
    A

    3厘米

    B

    9厘米

    C

    27厘米


    正确答案： B
    解析： 暂无解析

相关内容