有n对变量值(Xi，Yi)建立直线回归方程，要求

题目

有n对变量值(Xi，Yi)建立直线回归方程，要求

相似考题

1.两个变量(x，y)，有n对观测值(xi，yi)，如果这n个点在直角坐标系中形成一条直线，则相关系数r的取值为( )。A．r＝1B．r＝0C．r＝-1D．r＞0E．r＝2

2.在yi准确的前提下,即yi=y(xi)时,用数值方法计算yi+1的误差Ri=y(xi+1)–yi+1,称为该数值方法计算yi+1时的局部截断误差。()

3.有n对变量值(Xi,yi)建立直线回归方程,要求A.使∑(Xi一xi)最小 B.使∑(Xi—yi)2最小 S有n对变量值(Xi，yi)建立直线回归方程，要求A.使∑(Xi一xi)最小B.使∑(Xi—yi)2最小C.使∑(yi—Yi)2最小D.使∑(Xi一xi)2最小E.使∑(yi—yi)2最小

4.收集了n组数据(Xi，Yi)，i＝1，2，…，n，画出散布图，若n个点基本在——条直线附近时，称两个变量具有( )。A．独立关系B．不相容关系C．函数关系D．线形相关关系

参考答案和解析
正确答案：C
更多“ 有n对变量值(Xi，Yi)建立直线回归方程，要求 ”相关问题

  • 第1题：

    某公司编制的资金需要量预测表如下：

    年度 产销量（Xi）（万件） 资金占用（Yi）（万元） XiYi Xi2 2003 19 73 1387 361 2004 20 75 1500 400 2005 22 80 1760 484 2006 21 77 1617 441 2007 23 82 1886 529 合计n=5 ∑Xi=105 ∑Yi=387 ∑XiYi=8150 ∑Xi2=2215

    要求：

    （1）利用回归直线法确定资金需要量与产销量的线性关系方程；

    （2）如果预计2008年的产销量为25万件，计算2008年资金需要量。


    正确答案：
    (1)a＝(2215×387—105×8150)/(5×2215—105×105)＝(857205—855750)/(11075—11025)=29.1 
    b＝(5×8150—105×387)/(5×2215—105×105)=(40750—40635)/50=2.3 
    即：资金需要量与产销量的线性关系方程为y=29.1+2.3X 
    (2)预计2008年资金需要量＝29.1+2.3×25＝86.6(万元) 

  • 第2题：

    在一元线性回归中，给出n对数据(xi，yi)，i=1，2，…，n，若其回归方程为bx，则下述结论成立的有( )。

    A．总离差平方和ST=Lyy

    B．回归平方和SR=bLxy

    C．残差平方和SE=ST-SR)

    D．残差平方和的自由度为n-1

    E．残差平方和Se=ST-Sf


    正确答案：ABC
    解析：残差平方和的自由度为fE=n-2。

  • 第3题：

    若收集了n组数据(xi，yi)，i=1，2，…，n，并求得Lxx=330，Lxy=168，如Lyy= 88.9，则一元线性回归方程(作图)中的b=( )。

    A．0.5091

    B．0.5292

    C．1.8898

    D．1.9643


    正确答案：A
    解析：

  • 第4题：

    根据18对观测值（xi，yi)，i=1,2，…，18，建立了一光线性回归方程。在对该回归方程作显著性检验时,其回归平方和的自由度fR与残差平方和的自由度fE分别为（ ）
    A.fR=1

    B.fR= 2

    C.fE=18

    D.fE=17

    E.fE=16


    答案：A,E
    解析：
    。fE=n-2=18-2=16

  • 第5题：

    设X1,2X,…,Xn（n>2）相互独立且都服从N(0,1),Yi=Xi-X（i=1,2,…,n）.求：
    　　(1)D(Yi)(i=1,2,…,n);(2)Cov(Y1,Yn);(3)P(Yn+Yn≤0).


    答案：
    解析：

  • 第6题：

    两个变量(x，y)，有n对观测值(xi，yi)，如果这n个点在直角坐标系中形成一条直线，则相关系数，的取值为（）。

    • A、r=1
    • B、r=0
    • C、r=-1
    • D、r>0
    • E、不能确定

    正确答案:C

  • 第7题：

    数字地面模型DTM是表示区域D上地形的三维向量有限序列{Vi=（Xi，Yi，Zi），i=1，2，…n}，其中Zi是（Xi，Yi）对应的高程。


    正确答案:错误

  • 第8题：

    单选题
    一元线性回归模型的总体回归直线可表示为（　　）。
    A

    E（yi）＝α＋βxi

    B

    y(∧)i＝α(∧)＋β(∧)xi

    C

    yi＝α(∧)＋β(∧)xi＋ei

    D

    yi＝α＋βxi＋mi


    正确答案： A
    解析：
    对一元线性回归方程yi＝α＋βxi＋mi两边同时求期望，则有E（yi）＝α＋βxi。表明点（xi，E（yi））在E（yi）＝α＋βxi对应的直线上，这条直线即为总体回归直线（或理论回归直线）。

  • 第9题：

    单选题
    对回归模型yi＝β0＋β1xi＋μi进行检验时，通常假定μi服从（　　）。
    A

    N（0，σ12）

    B

    t（n－2）

    C

    N（0，σ2）

    D

    t（n）


    正确答案： C
    解析：
    对回归模型yi＝β0＋β1xi＋μi进行检验时，假定每个μi（i＝1，2，3，…，n）均为独立同分布，是服从正态分布的随机变量，且E（μi）＝0，V（μi）＝σμ2＝常数，即μi～N（0，σ2）。

  • 第10题：

    单选题
    收集了n组数据（xi，yi），i=1，2，…，n，画出散布图，若n个点基本在一条直线附近时，称两个变量间具有（　　）。
    A

    独立的关系

    B

    不相容的关系

    C

    函数关系

    D

    线性相关关系


    正确答案： C
    解析：
    若n个点基本在一条直线附近时，则两个变量间具有线性相关关系。

  • 第11题：

    判断题
    数字地面模型DTM是表示区域D上地形的三维向量有限序列{Vi=（Xi，Yi，Zi），i=1，2，…n}，其中Zi是（Xi，Yi）对应的高程。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第12题：

    单选题
    一元线性回归模型的总体回归直线可表示为（　　）。[2016年5月真题]
    A

    E（yi）＝α＋βxi

    B

    y(∧)i＝α(∧)＋β(∧)xi

    C

    yi＝α(∧)＋β(∧)xi＋ei

    D

    yi＝α＋βxi＋mi


    正确答案： D
    解析：
    对一元线性回归方程yi＝α＋βxi＋mi两边同时求期望，则有E（yi）＝α＋βxi。表明点（xi，E（yi））在E（yi）＝α＋βxi对应的直线上，这条直线即为总体回归直线（或理论回归直线）。

  • 第13题：

    在一元线性回归中，给出n对数据(xi，yi)，i=1，2，…，n，若其回归方程为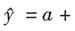bx，则下述结论不成立的有( )。

    A．总偏差平方和ST=Lyy

    B．回归平方和SR=b×Lxy

    C．残差平方和SE=ST-SR

    D．残差平方和的自由度为n-1


    正确答案：D
    解析：总偏差平方和的自由度fr=n-1，回归平方和的自由度fR=1，所以残差平方和的自由度fE=fT-fR=n-2。

  • 第14题：

    在一元线性回归中，给出n对数据(xi，yi)，i=1，2…，n，若其回归方程为，则下述结论成立的有( )。

    A．总偏差平方和ST＝Lyy

    B．归平方和SR＝bLxy

    C．残差平方和Se＝ST-SR

    D．残差平方和的自由度为n-1

    E．残差平方和Se＝ST-Sf


    正确答案：ABC

  • 第15题：

    若收集了n组数据(xi,yi), i =1， 2，…n，并求得Lxx=330，Lxy=168，Lyy=88.9，则一元线性回归方程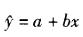中的b=( )。
    A. 0.5091 B. 0.5292 C. 1. 8898 D. 1.9643


    答案：A
    解析：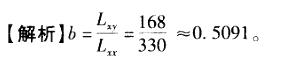

  • 第16题：

    设X1,X2,…,Xn（n>2）是来自总体X～N(0,1)的简单随机样本,记Yi=Xi-（i=1,2,…,n）.求：(1)D(Yi);(2)Cov(Yb,Yn).


    答案：
    解析：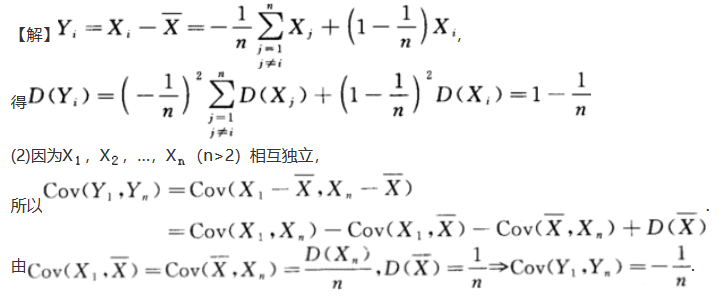

  • 第17题：

    对于yi=β0+β1xi这个式子的说法，正确的有（ ）。

    A.这是y对x的一元线性回归方程
    B.式中β0、β1是两个未知常数
    C.β1表示直线在y轴上的截距
    D.β0为直线的斜率
    E.β0、β1一旦确定这条直线也就唯一确定了

    答案：A,B,E
    解析：
    本题考查y对x的一元线性回归方程。β0表示直线在Y轴上的截距，β1为直线的斜率。选项CD的说法反了。

  • 第18题：

    根据闭合导线点坐标，可用（）公式计算其闭合图形内的面积A。

    • A、A=∑（xi-l-xi）（yi-1-yi）
    • B、2A=∑xi（yi-l-yi+1）
    • C、A=∑xi （yi-yi-1）
    • D、2A=∑yi（xi-xi-1）

    正确答案:B

  • 第19题：

    逐点比较法直线插补的偏差判别式函数为：F=Xi2+Yi2-D2。


    正确答案:错误

  • 第20题：

    单选题
    一元线性回归模型的总体回归直线可表示为（　　）。
    A

    E（yi）＝α＋βxi

    B

    y(∧)i＝α(∧)＋β(∧)xi

    C

    y(∧)i＝α(∧)＋β(∧)xi＋ei

    D

    y(∧)i＝α＋βxi＋μi


    正确答案： B
    解析：
    对一元回归方程Yi＝α＋βXi＋μi两边同时取均值，则有E（yi）＝α＋βxi。这表明点（xi，E（yi））在E（yi）＝α＋βxi对应的直线上，这条直线叫做总体回归直线（或理论回归直线）。

  • 第21题：

    单选题
    在对两个变量x，y进行线性回归分析时，有下列步骤：  ①对所求出的回归直线方程作出解释； ②收集数据（xi，yi），1，i=2，…，n； ③求线性回归方程；  ④求未知参数；  ⑤根据所搜集的数据绘制散点图  如果根据可行性要求能够作出变量x，y具有线性相关结论，则在下列操作中正确的是（）
    A

    ①②⑤③④

    B

    ③②④⑤①

    C

    ②④③①⑤

    D

    ②⑤④③①


    正确答案： D
    解析： 暂无解析

  • 第22题：

    单选题
    根据闭合导线点坐标，可用（）公式计算其闭合图形内的面积A。
    A

    A=∑（xi-l-xi）（yi-1-yi）

    B

    2A=∑xi（yi-l-yi+1）

    C

    A=∑xi （yi-yi-1）

    D

    2A=∑yi（xi-xi-1）


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    收集了n组数据(Xi，Yi)，i=1，2，…，n，画出散布图，若n个点基本在一条直线附近时，称两个变量具有(　　)。
    A

    独立关系

    B

    不相容关系

    C

    函数关系

    D

    线性相关关系


    正确答案： D
    解析： 暂无解析

相关内容