(Ⅱ)求甲获得这次比赛胜利的概率。
题目
(Ⅱ)求甲获得这次比赛胜利的概率。
相似考题
更多“(Ⅱ)求甲获得这次比赛胜利的概率。”相关问题
-
第1题:
某场羽毛球单打比赛采取三局两胜制。假设甲选手在每局都有80%的概率赢乙选手,那么这场单打比赛甲有多大的概率战胜乙选手:A. 0.768
B. 0.800
C. 0.896
D. 0.924答案:C解析:概率问题。分析甲获胜的情况可得:所求概率=0.8×0.8+0.8×0.2×0.8+0.2×0.8×0.8=0.896。因此,本题答案为C选项。 -
第2题:
甲、乙、丙、丁4个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这4个队分成两个组(每组两个队)进行比赛,胜者再赛,则甲、乙相遇的概率为( )A.1/6
B.1/4
C.1/5
D.1/3
E.1/2答案:E解析:
-
第3题:
某次网球比赛的四强对阵为甲对乙、丙对丁,两场比赛的胜者将争夺冠军.选手之间相互获胜的概率如下:

甲获得冠军的概率为A.0.165
B.0.245
C.0.275
D.0.315
E.0.330答案:A解析:第一局甲获胜的概率为0.3;第二局甲获胜的概率为0.3×0.5+0.8×0.5=0.55.故甲最终获胜的概率为0.3×0.55=0.165. -
第4题:
甲和乙进行打靶比赛,各打两发子弹,中靶数量多的人获胜。甲每发子弹中靶的概率是60%,而乙每发子弹中靶的概率是30%。则比赛中乙战胜甲的可能性为:
A小于5%
B在5%~10%之间
C在10%~15%之间
D大于15%答案:C解析:
-
第5题:
甲和乙进行5局3胜的乒乓球比赛,甲每局获胜的概率是乙每局获胜概率的1.5倍。问以下哪种情况发生的概率最大?A.比赛在3局内结束
B.乙连胜3局获胜
C.甲获胜且两人均无连胜
D.乙用4局获胜答案:A解析:第一步,本题考查概率问题。
第二步,根据甲获胜的概率是乙获胜概率的1.5倍,令乙获胜的概率为2x,则甲为3x,又甲获胜的概率和乙获胜的概率总和为1,可列式2x+3x=1,解得x=20%,则乙获胜的概率为40%,甲获胜的概率为60%。
第三步,选项信息充分,采用代入排除法解题。
代入A选项,比赛在3局内结束,则情况为甲前3局获胜或乙前3局获胜,概率为
(60%)^3+(40%)^3;
代入B选项,乙连胜3局获胜,情况有三种:乙前3局连胜、乙第一局输后面的三局连胜、乙前两局输后面的三局连胜,概率为(40%)^3+60%×(40%)^3+60%×60%×(40%)3;
代入C选项,甲获胜且两人均无连胜,则情况只有一种:甲胜乙胜甲胜乙胜甲胜,概率为60%×40%×60%×40%×60%;
代入D选项,乙用4局获胜,则情况为前3局乙胜2局,最后一局为乙胜,概率为;
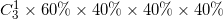
AB选项计算方式接近,优先进行比较:
(60%)^3+(40%)^3>60%×(40%)^3+60%×60%×(40%)3,排除B选项。
CD选项计算方式接近,优先进行比较。D选项数据>C选项数据,排除C选项。
AD比较,(60%)^3+(40%)^3>
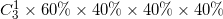
-
第6题:
李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过的0.6概率:
(3)记x是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这比赛中的命中次数,比较E(x)与x的大小(只需写出结论)。答案:解析:(1)根据投篮统计数据,在10场比赛中,李明投篮命中率超过0.6的场次有5场,分别是主场2,主场3,主场5.客场2。客场4。
所以在随机选择的一场比赛中,李明的投篮命中率超过0.6的概率是0.5。
(2)设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”.
事件曰为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”.
事件C为“在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6”.
所以,在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6的概率为13/25.
(3)
-
第7题:
在足球比赛中,防守是获得胜利的主要方法。
正确答案:错误 -
第8题:
甲投中篮球的概率0.5,乙投中的概率是0.6,各投两次,求甲乙投中次数相同的概率是()。
- A、0.63
- B、0.37
- C、0.36
- D、0.64
正确答案:B -
第9题:
甲和乙进行打靶比赛,各打两发子弹,中靶数量多的人获胜。甲每发子弹中靶的概率是60%,而乙每发子弹中靶的概率是30%。则比赛中乙战胜甲的可能性()
- A、小于5%
- B、在5%~12%之间
- C、在10%~15%之间
- D、大于15%
正确答案:C -
第10题:
判断题在足球比赛中,防守是获得胜利的主要方法。A对
B错
正确答案: 对解析: 暂无解析 -
第11题:
问答题22.甲、乙两人独立地各向同一目标射击一次,其命中率分别为0.6和O.7,求目标被命中的概率.若已知目标被命中,求它是甲射中的概率.正确答案:解析: -
第12题:
判断题羽毛球比赛打到20平时,必须某方运动员先打到30分时,方能获得本局比赛的胜利。A对
B错
正确答案: 错解析: 暂无解析 -
第13题:
速算比赛,小李全对的概率为95%,小杨全对的概率为92%,问这次比赛两人中只有一个人全对的概率为:
A0.046
B0.076
C0.122
D0.874答案:C解析:
-
第14题:
在某届洲际杯足球大赛中,第一阶段某小组单循环赛共有4支队伍参加,每只队伍需要再这一阶段比赛三场。甲国足球队在该小组的前两轮比赛中一平一负。在第三轮比赛之前,甲国足球队教练在新闻发布会上表示:"只有我们在下一场比赛中获得胜利并且本组的另外一场比赛打成平局,我们才有可能从这个小组出线。"A.甲国队第三场比赛取得了胜利,但他们未能从小组出线。
B.第三轮比赛该小组另外一场比赛打成平局,甲国队从小组出线。
C.第三轮比赛该小组两场比赛都分出了胜负,甲国队从小组出线。
D.第三轮比赛甲国队取得了胜利,该小组另一场比赛打成平局,甲国队未能从小组出线。
E.第三轮比赛该小组两场比赛都打成了平局,甲国队未能从小组出线答案:A解析: -
第15题:
甲乙比赛围棋,约定先胜2局者胜,已知每局甲胜概率0.6,乙为0.4,若第一局乙胜,则甲赢得比赛概率为A.0.144
B.0.288
C.0.36
D.0.4
E.0.6答案:C解析: -
第16题:
使用正态分布表,可以进行的计算有( )A.根据Z分数求概率
B.根据概率求Z分数
C.根据概率求概率密度
D.根据Z值求概率密度答案:A,B,C,D解析:本题考查的是正态分布表的应用:(1)已知Z分数求概率,即已知标准分数求面积,有三种情况:①求某Z分数值与平均数之间的概率;②求某Z分数以上或以下的概率;③求两个Z分数之间的概率。(2)已知概率求z分数,即从面积求标准分数值,也有三种情况:①已知从平均数开始的概率值求Z值;②已知位于正态分布两端的概率值求该概率值分界点的Z值;③若已知正态曲线下中央部分的概率,求Z分数是多少。(3)已知概率或标准分数可查密度值、函数值。 -
第17题:
甲、乙两人进行五子棋比赛,必须要经过A、B、C三场比赛的角逐,甲对乙每局获胜的概率 为60%,乙对甲每局获胜的概率为40%,则甲胜出的可能性为( )。
A.小于15%
B.介于15%--40%内
C.介于40%--60%内
D.大于60%答案:D解析:本题考查了分步计数原理和分类计数原理。甲胜出的可能情况有两种: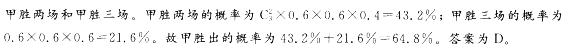
-
第18题:
李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):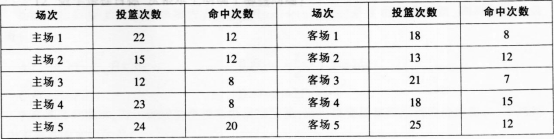
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率。
(2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率。答案:解析:

-
第19题:
速算比赛,小李全对的概率为95%,小杨全对的概率为92%,问这次比赛两人中只有一个人全对的概率为:
- A、0.046
- B、0.076
- C、0.122
- D、0.874
正确答案:C -
第20题:
羽毛球比赛打到20平时,必须某方运动员先打到30分时,方能获得本局比赛的胜利。
正确答案:错误 -
第21题:
为丰富员工业余文化生活,某单位组织了乒乓球、象棋、羽毛球三项比赛。每两个人之间都要通过比试这3项分出胜负,假设没有平局,同时比赛的2个人甲和乙,甲在乒乓球战胜乙的概率是50%、甲在象棋战胜乙的概率是50%、甲在羽毛球战胜乙的概率是40%,那么比试下来,甲战胜乙的概率是()
- A、0.3
- B、0.35
- C、0.4
- D、0.45
正确答案:D -
第22题:
问答题求下列事件的概率: (1)n(n>3)个人坐成环形,求甲、乙、丙三个人坐在一起的概率; (2)n(n>3)个人并排坐,求甲、乙、丙三个人坐在一起的概率。正确答案:
(1)设事件N表示“甲、乙、丙三人坐在一起”,n个人坐成环形共有n!/n=(n-1)!种坐法,甲、乙、丙三人坐在一起,那么可以将他们看作一个整体,共有(n-2)!A33/(n-2)=(n-3)!A33种坐法。P(N)=(n-3)!A33/(n-1)!=6/[(n-1)(n-2)]。
(2)n个人坐成一排共有n!种不同坐法,仍将甲、乙、丙三人看作一个整体,共有(n-2)!A33种坐法,所以P(A)=(n-2)!A33/n!=6/[n(n-1)]。解析: 暂无解析 -
第23题:
单选题速算比赛,小李全对的概率为95%,小杨全对的概率为92%,问这次比赛两人中只有一个人全对的概率为( )A0.046
B0.076
C0.122
D0.874
正确答案: A解析:
