一个直角三角形三条边的长度是3、4、5，如果分别以各边为轴旋转一周，得到三个立体。三个立体中最大的体积和最小的体积的比为（ ）。A．3：2B．2：1C．5：3D．5：4

题目

一个直角三角形三条边的长度是3、4、5，如果分别以各边为轴旋转一周，得到三个立体。三个立体中最大的体积和最小的体积的比为（ ）。

A．3：2

B．2：1

C．5：3

D．5：4

相似考题

1.若等腰直角三角形的直角边长为2，则以一直角边所在的直线为轴旋转一周所成的几何体体积是 。

2.(1)黄强上前拦住老人 (2)一位老人在门岗前骑车前行(3)一边解释一边敬礼 (4)老人犟劲上来了，硬要往前闯(5)被三个敬礼感动了A．4-3-1-2-5B．4-2-3-1-5C．2-3-4-1-5D．2-1-4-3-5

3.从长度分别为2、3、4、5的四条线段中任意取出三条，则以这三条线段为边可以构成三角形的概率是________。

4.△ABC三个顶点坐标分别为A（2,2），B（4,2），C（6，4），以原点O为位似中心，将△ABC缩小后得到的△DEF 与△ABC对应边的比为1:2，这时△DEF各个顶点的坐标分别是多少？

更多“一个直角三角形三条边的长度是3、4、5,如果分别以各边为轴旋转一周,得到三个立体。三个立 ”相关问题

  • 第1题：

    如图所示，一个小区的道路围成了一个五边形，经实地勘测，五边形内有三个角为直角，AD 边、BC 边和 CD 边长度相等，且 OA 边长度为其一半。 已知 AD 边长 20 米，问道路围成的五边形面积为多少



    答案：D
    解析：
    将五边形分割成四边形ABCD和三角形AOB求解。由题意知，四边形ABCD是边长为20米的正方形，三角形AOB是直角三角形，因为OA＝(1/2)AB＝10米，所以米，则五边形的面积为平方米。故本题选D。

  • 第2题：

    如图，已知图中四边形两条边的长度和三个角的度数，四边形ABCD的面积是______cm2。


    答案：
    解析：
    24。解析：延长AD和BC交于点E，则得到两个等腰直角三角形△ABE和△DCE，四边形ABCD

  • 第3题：

    设的三条边分别是a，b，C，且a2+b2=c2。证明：ΔABC是直角三角形。(这是勾股定理的逆命题)


    答案：
    解析：
    证明．以n．b长为直角边作Rt△A，B，C．设斜边长为d．则由勾股定理得

    全等．故ABC是直角三角形。

  • 第4题：

    计算题：用84cm长的圆钢围成一个三角形支架，这个三角形的三条边之比为3：4：5，问三条边各是多少？


    正确答案: 设最长边为a，次长边位b，最短边位c。
    则a=84×[5/（3+4+5）]=35（cm）
    b=84×[4/（3+4+5）]=28（cm）
    c=84×[3/（3+4+5）]=21（cm）

  • 第5题：

    正圆锥可以定义为一个直角三角形绕其一条直角边旋转一周得到的几何体，它可以由平面截（）得到。


    正确答案:圆锥面

  • 第6题：

    以直角三角形的直角边所在直线为旋转轴，其余两边旋转360度形成一个几何体，若将该几何体的侧面沿母线展开，则其展开图是（）


    正确答案:扇形

  • 第7题：

    有一个内角为30°的直角三角形的斜边为5，那么30°内角所对应的边的长度为（）。

    • A、5
    • B、2.5
    • C、3
    • D、3.5

    正确答案:B

  • 第8题：

    对于矩形区域内的常物性，无内热源的导热问题，试分析在下列四种边界条件的组合下，导热物体为铜或钢时，物体中的温度分布是否一样： （1）四边均为给定温度； （2）四边中有一个边绝热，其余三个边均为给定温度； （3）四边中有一个边为给定热流（不等于零），其余三个边中至少有一个边为给定温度； （4）四边中有一个边为第三类边界条件。


    正确答案: （1）一样，因为两种情况下的数学描写中不出现材料物性值；
    （2）一样，理由同上；
    （3）不一样，在给定热流的边上，边界条件中出现固体导热系数；
    （4）不一样，在第三类边界条件的表达式中出现固体导热系数。

  • 第9题：

    判断题
    分别以直角三角形的三边为边向外作三个相似的多边形，则两直角边上的多边形的面积之和等于斜边上的多边形的面积。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第10题：

    问答题
    师：下列长度的三条线段能组成三角形吗?请快速抢答，并简单说明判断过程。(1)2Cm，4Cm，5Cm(2)2Cm，2Cm，4Cm(3)lCm，5Cm，3Cm生1：(1)、(3)可以组成一个三角形。(2)不能组成三角形。师：为什么呢?生1：根据两条边之和大于第三条边。2+4大于5，2+2不大于4，1+5大于3。师：大家同意吗?生2：我认为(3)不能组成三角形，因为l+3不大于5。师：很好!大家对(1)、(2)没问题吧。对于(3)，大家同意吗?你认为应该验证三个不等式，如果我们只验证一个不等式，大家看看行吗?生3：应该是每两条边之和都应该大于第三条边。师：是吗?可是该怎样验证才最快啊?生1：定理说三角形两边之和大于第三边，应该任意两奈边才对，我看只须验证1+3不大于5，是最小两边之和不大于最大一边。师：非常好!大家看看，是吗?生：是的。师：好!我们考虑问题就是要这样，要全面、快速．要抓住关键的东西。问题：请对：上述案例进行评析。

    正确答案： 教师通过与学生的交流，给学生创造自我评价的机会，学生通过自我评价，体验到成功的喜悦。素质教育的一个亮点是突出学习者的主体地位，学习的过程是学生自己体验、领悟、积累的过程。多给学生创造ta我评价的机会，可以对学生的学习产生积极的影响。课堂教学即时评价能够激励、鼓舞、调动学生参与的热情，发掘学生的潜能，在教学中，课堂是活生生的学生思考的角度、速度是多种多样的，充满未知的因素，具有动态生成的特性，因此，教师充分开发利用课堂的突然的问题，并能瞬时作出即时评价，则会紧扣学生的思维，让课堂充满勃勃的生机。
    解析： 暂无解析

  • 第11题：

    单选题
    《高层民用建筑设计防火规范》规定，高层建筑的底边至少有一个长边或周边长度的1/4且不小于（）长度，不应布置高度大于5米、进深大于4米的裙房
    A

    一个短边

    B

    一个长边

    C

    1/3个长边

    D

    1/2个短边


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    直角三角形的两直角边分别为4cm和5cm，直角三角形的面积是（）cm2。
    A

    5

    B

    10

    C

    15

    D

    20


    正确答案： A
    解析： 暂无解析

  • 第13题：

    一个直角三角形的三条边分别是3厘米，4厘米，5厘米(如图)，如果以它的最长边为轴旋转一周，求旋转后所形成图形的体积.(π取3计算)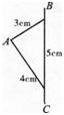


    答案：
    解析：



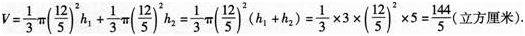
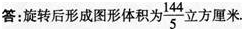
  • 第14题：

    一个直角三角形三条边的长度是3，4，5，如果分别以各边为轴旋转一周，得到三个立方体，则三个立方中最大的体积和最小的体积的比为（ ）。
    A. 3：2 B. 2：1 C. 5：3 D. 5：4


    答案：C
    解析：

  • 第15题：

    《高层民用建筑设计防火规范》规定，高层建筑的底边至少有一个长边或周边长度的1/4且不小于（）长度，不应布置高度大于5米、进深大于4米的裙房

    • A、一个短边
    • B、一个长边
    • C、1/3个长边
    • D、1/2个短边

    正确答案:B

  • 第16题：

    正面清洗人员需检查硅胶固化情况，必须用手按压三个点，分别是中间两边各一个点


    正确答案:错误

  • 第17题：

    一个长方形以一边为轴顺时针或逆时针旋转一周，所形成的立体图形的侧面积=（）×高。


    正确答案:底面周长

  • 第18题：

    分别以直角三角形的三边为边向外作三个相似的多边形，则两直角边上的多边形的面积之和等于斜边上的多边形的面积。


    正确答案:错误

  • 第19题：

    B25包装机内衬纸折叠传动箱通过（）凸轮分别带动三个执行机构：内衬纸旋转挡板、内衬纸顶底长边折叠器和内衬纸第四工位顶底短边折叠器。

    • A、一个
    • B、两个
    • C、三个
    • D、四个

    正确答案:C

  • 第20题：

    填空题
    叶片式流体机械的速度三角形中有三条边，这三条边对应三个矢量，它们分别是（）、（）和（）矢量。

    正确答案： 绝对速度,相对速度,圆周速度（牵连速度）
    解析： 暂无解析

  • 第21题：

    单选题
    有一个内角为30°的直角三角形的斜边为5，那么30°内角所对应的边的长度为（）。
    A

    5

    B

    2.5

    C

    3

    D

    3.5


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    有五条长度不等的线段，其长度分别为1，3，5，7，9个单位，从中任取三条作边，能组成三角形的概率等于(　　)．
    A

    4

    B

    2

    C

    3

    D

    7


    正确答案： C
    解析： 根据三角形的性质可以得知。

  • 第23题：

    单选题
    最或是船位在随机船位误差三角形之内（）。
    A

    三条反中线的交点上

    B

    靠近短边，大角

    C

    距各边的距离与各边的长度成正比

    D

    以上均对


    正确答案： A
    解析： 暂无解析

相关内容