李某向银行贷款30万元购买了一套住宅,该笔贷款的期限为20年,贷款年利润为6%,按月等额还本付息。如果李某于11年年初一次性提前偿还本金10万元,则从第11年开始的月还款额为( )元。 A.948.72 B.1039.09 C.1200.58 D.2149.29
题目
B.1039.09
C.1200.58
D.2149.29
相似考题
更多“李某向银行贷款30万元购买了一套住宅,该笔贷款的期限为20年,贷款年利润为6%,按月等额还本付息。如果李某于11年年初一次性提前偿还本金10万元,则从第11年开始的月还款额为( )元。 ”相关问题
-
第1题:
某人准备购买一套价格为15万元的住宅,首期30%直接支付,其余向银行申请贷款,贷款期限为10年,利率9%,按月等额偿还,则月还款额为多少?若抵押贷款采用递增式还款(逐月递增0·5%),则首月还款额为多少?最后一月还款额为多少?如该家庭在按月等额还款5年后于第六年年初一次提前偿还了贷款本金5万元,则从第六年开始的抵押贷款月还款额是多少?
正确答案:
-
第2题:
某家庭以30万元购买了一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款。如果该家庭于第六年年初一次提前偿还贷款本金5万元,则从第六年开始的抵押贷款月还款额将减少( )元。
A.544.10
B.555.10
C.1776.32
D.2109.38
正确答案:B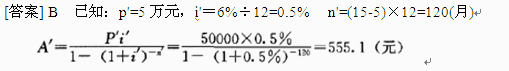
-
第3题:
某家庭以30万元购买一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款。如果该家庭于第6年初一次提前偿还贷款本金5万元。则从第6年开始的抵押贷款月还款额将减少()元。A:544.10
B:556.00
C:1776.32
D:2109.38答案:B解析:具体计算过程如下:①n1=15*12=180个月,n2=5*12=60个月,i=6%/12=0.5%;②初始抵押贷款数额为30万元,③该家庭月还本付息额为:A=P*i/[1-(1+i)-n]=30*05%/[1-(1+0.5%)-180]=0.2530(万元),④第6年初尚未偿还折抵押贷款本金额为:P=(A/i)*[1-(1+1)-n]=(0.2530/0.5%)*[1-(1+0.5%)-(180-60)]=22.77(万元);⑤当该家庭在第6年初一次偿还本金5万元后,则在第6年初尚未偿还抵押贷款本金数额为22.77-5=17.77(万元),⑥从第6年开始该家庭月还本付息额为:A1=P1*i/[1-(1+i)-n]=17.77*0.5%/[1-(1+0.5%)-120]=0.1974(万元);⑦从第6年开始的月还本付息额将减少:2530-1974=556(元)。 -
第4题:
赵某购买一套商品住宅,成交价格为50万元,首期付款为房价的30%,余款向银行抵押贷款。该贷款的贷款期限为10年,贷款年利率为6%,采用按月等额还款方式偿还。若第6年初赵某决定提前偿还全部贷款余额,此时的贷款余额为( )元。A、172858
B、182786
C、192858
D、201006答案:D解析:考点:复利系数的应用。实质:贷款余额=第6年至第10年的年值,折现到第5年年末时的现值。
第一步,已知贷款P,先求出月还款额A。
P=50×(1-30%)=35(万元),i月=6%/12=0.5%,n=10×12=120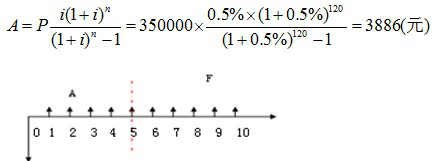
第二步,把第六年到第十年的年值(月供),折现到第五年年末,已知n=10×12=120,m=5×12=60,n-m=60,P=A/i×[1-1/(1+i)n]=3886/0.5%×[1-1/(1+0.5%)60]=201005.53元。 -
第5题:
某家庭以80万元购买了一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款,如果该家庭于第6年初一次提前偿还贷款本金10万元,则从第6年开始的抵押贷款月还款额将减少( )元。A、1110.21
B、1244.10
C、1776.32
D、2109.38答案:A解析:本题考查的是复利系数的应用。将第6年初的10万元看作P,在余下的10年中每月等额还款数就是从第6年开始的抵押贷款月还款额减少值。月利率=6%÷12=0.5%,运用公式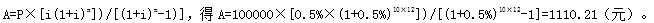
-
第6题:
某家庭申请了50万元10年期住房抵押贷款,年利率为6%。该家庭在按月等额偿还5年后于第6年初一次偿还了本金6万元,则从第6年开始该家庭的月还款额减少了( )元。A.984.37
B.1016.81
C.1159.97
D.2387.24答案:C解析:本题考查的是复利计算。月还款的减少额,就是提前还款的6万元转化为等价每月等额还款后的值。根据公式:P=A/i×[1-1/(1+i)^n],得:A=60000×6%/12÷[1-1/(1+6%/12)^60]=1159.97(元)。 -
第7题:
王某购买一套商品住宅,成交价格为50万元,首期付款为房价的30%,余款向银行抵押贷款。该贷款的贷款期限为10年,贷款年利率为6%,采用按月等额还款方式偿还。若第5年末王某决定提前偿还全部贷款余额,此时的贷款余额为多少元答案:解析:贷款余额=第6年至第10年的年值,折现到第5年年末时的现值。
第一步,已知贷款P,先求出月还款额A
P=50×(1-30%)=35(万元)=350000(万元)
i月=6%/12=0.5%,n=10×12=120
A=P×i(1+i)n/[(1+i)n-1]=350000×0.5% (1+0.5%)120/[(1+0.5%)120-1]=3886(元)
第二步,把第六年到第十年的年值(月供),折现到第五年年末
已知n=10×12=120,m=5×12=60,n-m=60
Pn=A[((1+i)n-m-1)/[i(1+i)n-m]=3886[((1+0.5%)60-1)/[0.5%(1+0.5%)60]=201006(元)=20.1(万元) -
第8题:
(2016年真题) 李某向银行贷款30万元购买了一套的住宅,该笔贷款的期限为20年,贷款年利润为6%,按月等额还本付息。如果李某于11年年初一次性提前偿还本金10万元,则从第11年开始的月还款额为( )元。A.948.72
B.1039.09
C.1200.58
D.2149.29答案:B解析:本题考查的是复利系数的应用。月利率=6%/12=0.5%,n=12×20=240个月,P=30万元,A1=P[i(1+i)n]/[(1+i)n-1]=300000[0.5%(1+0.5%)240]/[(1+0.5%)240-1]=2149.293元,第11年年初一次性提前偿还本金10万元,折算为第11年年初至第20年每月的额度为A2=100000[0.5%(1+0.5%)120]/[(1+0.5%)120-1]=1110.205元,则从第11年开始的月还款额为A=A1-A2=2149.293-1110.205=1039.09元。@## -
第9题:
王某购买一套商品住宅,成交价格为100万元,首期付款为房价的30%,余款向银行抵押贷款。该贷款的贷款期限为10年,贷款年利率为6%,采用按月等额还款方式偿还。王某的月还款额为()元。
- A、3884
- B、5668
- C、7772
- D、9336
正确答案:C -
第10题:
计算题:某家庭购买了一套90m2的商品住宅,售价为4000元/m2。该家庭首付了房价总额的30%,其余购房款申请住房公积金和商业组合抵押贷款。住房公积金贷款和商业贷款的利率分别是4.5%和6.8%,贷款期限为15年,按月等额偿还。其中住房公积金贷款的最高限额为10万元。如果该家庭以月收入的35%用来支付抵押贷款月还款额,那么此种贷款方案要求该家庭的最低月收入为多少?假设该家庭在按月还款3年后,于第4年初一次性提前偿还商业贷款本金5万元, 那么从第4年起该家庭的抵押贷款的月还款额为多少?
正确答案: (一)解法一:
(1)已知P=4000×90×(1-30%)=25.2万元
P1=10万元;P2=(25.2-10)=15.2万元
(2)N=15×12=180月
=4.5%/12=0.375%i2=6.8%/12=0.57%(0.567%,0.5667%)
A1=P1×[i1×(1-i1)n]/[(1+i1)n-1]=10000×[0.375%×(1+0.375%)180]/[(1+0.375%)180-1]
=764.99元
Al=P2×[i2×(1-i2)n]/[(1+i2)n-1]=15200×[0.57%×(1+0.57%)180]/[(1+0.57%)180-1]
=1352.66元(按照0.57%)
=1349.62元(按照0.567%)
=1349.31元(按照0.5667%)
A=A1+A2=764.99+1352.66=2117.65元(按照0.57%)
=2114.61元(按照0.567%)
=2114.3元(按照0.5667%)
(3)最低月收入=A/0.35=2117.65/0.35=6050.43元(按照O.57%)
=6041.74元(按照0.567%)
=6040.86元(按照0.5667%)
(4)第4年初一次偿还商贷本金5万元,在第4年第15年内的月还款额为:
P1=5万元n=(15-3)×12=144月
A’=P×P2×[i2(1+i2)n]/[(1+i2)n-1]
=5×[O.57%×(1+O.57)n]/[(1+O.57%)n-1]
=509.94元(按照O.57%)
=508.98元(按照0.567%)
=508.89元(按照0.5667%)
从第4年起抵押贷款月还款额为:A-A’=2117.65-509.94=1607.71元(按照O.57%)
(二)解法二:
(1)~(3)与解法一相同
(4)还款3年后,尚未偿还商业贷款n=(15-3)×12=144月
(5)第4年初还款5万元后,商业贷款月还款额A:
P3=132630.40-50000=82630.4元
A3=82630.4[O.57%×(1+O.57%)144]/[(1+O.57%)144-1]=842.72
(6)该家庭第4年初的月还款额为:
A1+A2=764.99+842.72=1607.71元 -
第11题:
单选题某家庭以30万元购买一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款。如果该家庭于第6年初一次提前偿还贷款本金5万元。则从第6年开始的抵押贷款月还款额将减少( )元。A544.10
B556.00
C1776.32
D2109.38
正确答案: A解析:
具体计算过程如下:
①n1=15×12=180个月,n2=5×12=60个月,i=6%/12=0.5%;
②初始抵押贷款数额为30万元;
③该家庭月还本付息额为:A=P×i/[1-(1+i)-n]=30×0.5%/[1-(1+0.5%)-180]=0.2530(万元);
④第6年初尚未偿还折抵押贷款本金额为:P=(A/i)×[1-(1+i)-n]=(0.2530/0.5%)×[1-(1+0.5%)-(180-60)]=22.77(万元);
⑤当该家庭在第6年初一次偿还本金5万元后,则在第6年初尚未偿还抵押贷款本金数额为22.77-5=17.77(万元);
⑥从第6年开始该家庭月还本付息额为:A1=P1×i/[1-(1+i)-n]=17.77×0.5%/[1-(1+0.5%)-120]=0.1974(万元);
⑦从第6年开始的月还本付息额将减少:2530-1974=556(元)。 -
第12题:
单选题李某从银行贷款56万元购买了一套住宅,该笔贷款的期限为20年,年利率为7.5%,按月等额偿还。如果李某于第7年末提前偿还本金10万元,则从第8年开始的月还款额为( )元。A3456.09
B3505.95
C3509.74
D3705.73
正确答案: A解析: -
第13题:
李某从银行贷款56万元购买了一套住宅,该笔贷款的期限为20年,年利率为7.5%,按月等额偿还。如果李某于第7年末提前偿还本金10万元,则从第8年开始的月还款额为( )元。
A.3456.09
B.3505.95
C.3509.74
D.3705.73
正确答案:B
解析:
已知P=56万元,n=20*12=240,i=7.5%/12=0.625%
月等额还款A=pi/1-1/(1+i)^n=56*0.625%/[1-1/(1+0.625%)^240]=4511.32
又已知m=7*12=84,第8 年初未还贷款余额:
P’=A/i*[1-1/(1+i)^n-m]=4511.32/0.625%*[1-1/(1+0.625%)^240-84]=448722.1731
还10万,本金余额为348722.1731
再求第8年开始的月还款额为=348722.1731*0.625%/[1-1/(1+0.625%)^156]=3505.95(元) -
第14题:
某家庭以30万元购买了一套住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,按月等额还款,如果该家庭于第6年初一次提前偿还贷款本金5万元,则从第6年开始的抵押贷款月还款额将减少( )元。
A.544.10
B.555.10
C.1776.32
D.2109.38
正确答案:B
-
第15题:
共用题干
赵某购买一套商品住宅,成交价格为50万元,首期付款为房价的30%,余款向银行抵押贷款。该贷款的贷款期限为10年,贷款年利率为6%,采用按月等额还款方式偿还。赵某的月还款额为()元。
A:2974
B:3886
C:5356
D:9742答案:B解析:本题考查房地产抵押贷款中,不得作为抵押的财产。
本题考查房地产抵押的手续。房地产抵押必须经登记后方可生效。
本题考查房地产抵押登记的相关规定。房地产抵押登记后,登记机关应在原房屋所有权证书上作他项权利记载,由赵某继续持有房屋所有权证书,而向抵押权人(银行)颁发房屋他项权利证书。
本题考查等额还款抵押贷款中月还款额的计算。向银行贷款总额50*(1-30%)=35(万元)i=6%/12=0.5%,n=10*12=120A=P(A/P,i,n)=35(A/P,0.5%,120)=0.3886(万元)。
上题中已计算出每月的还款额,又知道赵某家庭收入的25%用于还款,所以赵某的家庭收入至少应该为3886/25%=15544(元)。
本题考查等额还款抵押贷款中贷款余额的计算。其实质是贷款余额=第6年至第10年的年值,折现到第5年年末时的现值。可直接套用公式:n=10*12=120,m=5*12=60,n-m=60Pm=A(P/A,i,n-m)=3886(P/A,0.5%,60)=3886*[(1+0.5%)60)-1]/[0.5(1+0.5%)60]=201006(元)。
提前还款是指借款人提前偿还贷款。一种可能是当市场利率下跌时,借款人有可能选择以当前市场上较低的利率重新借款,所以对已有的贷款会提出提前还款;另上种情况就是抵押人的收入水平上升,有足够的能力提前还款。 -
第16题:
某家庭以30万元购买了一套住宅,银行为其提供了20年期的住房抵押贷款,该贷款的年利率为9%,按月等额还款,如果该家庭于第6年年初一次提前偿还贷款本金7万元,则从第6年开始的抵押贷款月还款额将减少( )元。A、 544.10
B、 709.99
C、 6300.00
D、 709.38答案:B解析:将第6年年初的7万元看做P,在余下的10年中每月等额还款数就是从第6年开始的抵押贷款月还款额减少值。运用公式

可得:?
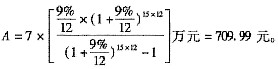
注意:公式中的n是15而不是14,因为第6年年初等于第5年年末。 -
第17题:
某家庭以抵押贷款的方式购买了一套价值为100万元的住宅,首付款为房价的50%,其余房款用抵押贷款支付。如果抵押贷款的期限为20年,按月等额偿还,年贷款利率为12%,问:
(1)抵押贷款额、月贷款利率与月还款额各为多少
(2)如果该家庭30%的收入可以用来支付抵押贷款月还款额,则该家庭须月收入多少,才能购买上述住宅
(3)如果该家庭在按月等额还款5年后,于第6年年初一次提前偿还剩余贷款本息,则还款额为多少答案:解析:(1)抵押贷款额P=100×50%=50万元;
月贷款利率i=12%/12=1%;
月还款额为:A=P×i(1+i)n/[(1+i)n-1]=50×1%(1+1%)240/[(1+1%)240-1]=0.550543万元=5505.43元;
(2)该家庭欲购买上述住宅,其月收入须为:5505.43/30%=18351.43元
(3)该家庭在第6年年初一次提前偿还剩余贷款余额时,所需偿还金额为
Pn=A[((1+i)n-m-1)/[i(1+i)n-m],其中,n=12×20=240,m=12×5=60,
代入数据,得到Pn=5505.43×[((1+1%)240-60-1)/[1%(1+1%)240-60]=458721.59元=45.87万元。 -
第18题:
某家庭申请了25万元10年期住房抵押贷款,年利率为6%。该家庭在按月等额偿还4年后于第5年初一次偿还了本金6万元,则从第5年开始该家庭的月还款额减少了( )元。A、 994.37
B、 1016.81
C、 1255.16
D、 1387.24答案:A解析:[解析] 复利系数的应用 -
第19题:
某家庭以4000元/m2的价格,购买了一套建筑面积为120m2的住宅,银行为其提供了15年期的住宅抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金8万元,问从第6年开始的抵押贷款月还款额是多少?答案:解析:
第二步,计算出第6年年初(也就是第五年年末)偿还的本金部分,在第6到第15年内减少的月还款额
第三步,计算从第6年开始抵押贷款月还款额
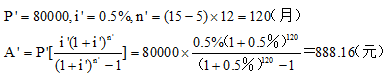
第三步,计算从第6年开始抵押贷款月还款额
-
第20题:
某家庭以2000元/m2的价格,购买了一套建筑面积为120m2的住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金4万元,那么从第6年开始的抵押贷款月还款额为( )元。A.1417.68
B.444.08
C.1861.76
D.973.60答案:D解析:本题考查的是资金等效值的换算。

-
第21题:
某家庭以住宅抵押贷款方式购买了一套住宅,住房抵押贷款期限为20年,年利率为6%,以每月5000元等额还款。该家庭于第9年初一次性偿还贷款本金10万元,余额在以后的5年内用按月等额还款的方式还清,则最后5年内的月等额还款额为( )元。
- A、7019.53
- B、7972.33
- C、8524.15
- D、8587.65
正确答案:B -
第22题:
某居民购买一套总价为30万元的商品住宅,首期付款为总价的30%,余款向银行贷款,贷款期限为20年,贷款年利率为6%,若按月等额偿还贷款本息,则该居民的月还款额为()元。
- A、1504.5
- B、1507.5
- C、1643.5
- D、1695.5
正确答案:A -
第23题:
问答题【例5-7】某家庭以4000元/㎡的价格,购买了一套建筑面积为120㎡的住宅,银行为其提供了15年期的住房抵押贷款,该贷款的年利率为6%,抵押贷款价值比率为70%。如该家庭在按月等额还款5年后,于第6年初一次提前偿还了贷款本金8万元,问从第6年开始的抵押贷款月还款额是多少?正确答案:解析:
