20212022学年度强化训练冀教版八年级数学下册第二十一章一次函数难点解析试卷(含答案详解)
司法考试前三卷都是选择题?
你好,是的,前三卷为选择题。
【题目描述】

这三个自然数分别是()
【参考答案分析】:

某考试卷中有若干选择题,每答对一题加2分,答错或不答一题扣1分,一考生答对的选择题数量是答错或不答的5倍,选择题共得到45分。问试卷中有多少道选择题?( )
A.50
B.30
C.25
D.20
这是一道和差倍比问题。
(1)设答错的题目数为x,则答对的题目数为5x,有2×5x-x=45,可得x=5,则答对的题目数为5×5=25,题目总数为5+25=30。因此,本题的正确答案为B选项。
(2)如果答对5题,答错1题,得分应该是9分。现在得了45分,因此试卷中有45/9×(5+1)=30道题目,选B选项。
请告诉我正确答案
把详细的具体问题发上来。才好解答啊。
【题目描述】
第 3 题
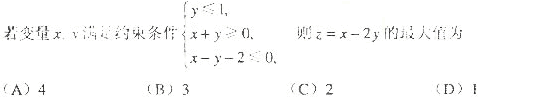
正确答案:B
八年级数学下册第二十一章一次函数难点解析 考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、已知一次函数,其中y的值随x值的增大而减小,若点A在该函数图象上,则点A的坐标可能是( )ABCD2、已知是一次函数,则m的值是( )A3B3C3D23、若直线ykxb经过一、二、四象限,则直线ybxk的图象只能是图中的( )ABCD4、如图,李爷爷要围一个长方形菜园ABCD,菜园的一边利用足够长的墙,用篱笆围成的另外三边的总长恰好为24m,设边BC的长为xm,边AB的长为ym(xy)则y与x之间的函数表达式为()Ay2x+24(0 x12)Byx+12(8x24)Cy2x24(0 x12)Dyx12(8x24)5、直线和在同一直角坐标系中的图象可能是( )ABCD6、甲、乙两地之间是一条直路,在全民健身活动中,王明跑步从甲地往乙地,陈启浩骑自行车从乙地往甲地,两人同时出发,陈启浩先到达目的地,两人之间的距离s(km)与运动时间t(h)的函数关系大致如图所示,下列说法中错误的是()A两人出发1小时后相遇B王明跑步的速度为8km/hC陈启浩到达目的地时两人相距10kmD陈启浩比王明提前1.5h到目的地7、甲、乙两车从城出发前往城,在整个行驶过程中,汽车离开城的距离与行驶时间的函数图象如图所示,下列说法正确的有()甲车的速度为;乙车用了到达城;甲车出发时,乙车追上甲车A0个B1个C2个D3个8、若一次函数的图像经过第一、三、四象限,则的值可能为( )A-2B-1C0D29、如图,甲乙两人沿同一直线同时出发去往B地,甲到达B地后立即以原速沿原路返回,乙到达B地后停止运动,已知运动过程中两人到B地的距离y(km)与出发时间t(h)的关系如图所示,下列说法错误的是()A甲的速度是16km/hB出发时乙在甲前方20kmC甲乙两人在出发后2小时第一次相遇D甲到达B地时两人相距50km10、在同一平面直角坐标系中,函数的图象与函数的图象互相平行,则下列各点在函数的图象上的点是( )ABCD第卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如果点P1(3,y1),P2(2,y2)在一次函数y=8x-1的图像上,那么y1_y2(填“”、“”或“=”)2、观察图象可以发现:直线yx,y3x向右逐渐_,即y的值随x的增大而增大;直线yx,y4x向右逐渐_,即y的值随x的增大而减小 3、在运用一次函数解决实际问题时,首先判断问题中的两个变量之间是不是_关系,当确定是一次函数关系时,可求出函数解析式,并运用一次函数的图象和性质进一步求得我们所需要的结果4、已知点A(2,a),B(3,b)在直线y2x3上,则a_b(填“”“”或“”号)5、若正比例函数ykx(k是常数,k0)的图象经过第一、三象限,请写出一个满足上述要求的k的值_三、解答题(5小题,每小题10分,共计50分)1、已知点,和直线,则点到直线的距离可用公式计算,例如:求点到直线的距离解:因为直线,其中,所以点到直线的距离:根据以上材料,解答下列问题:(1)求点到直线的距离(2)已知的圆心的坐标为,半径为,判断与直线的位置关系并说明理由(3)已知互相平行的直线与之间的距离是,试求的值2、已知一次函数在轴上的截距为2,且随的增大而减小,求一次函数的解析式,并求出它的图像与坐标轴围成的三角形的面积3、已知y与成正比例,且当时,;(1)求出y与x之间的函数关系式;(2)当时,求y的值;(3)当时,求x的取值范围4、在平面直角坐标系中,已知点A(4,0),点B(0,3)点P从点A出发,以每秒1个单位的速度向右平移,点Q从点B出发,以每秒2个单位的速度向右平移,又P、Q两点同时出发(1)连接AQ,当ABQ是直角三角形时,则点Q的坐标为 ;(2)当P、Q运动到某个位置时,如果沿着直线AQ翻折,点P恰好落在线段AB上,求这时AQP的度数;(3)若将AP绕点A逆时针旋转,使得P落在线段BQ上,记作P,且APPQ,求此时直线PQ的解析式5、辆货车从甲地到乙地,一辆轿车从乙地到甲地,两车沿同一条公路分别从甲、乙两地同时出发,匀速行驶已知轿车比货车每小时多行驶20km;两车相遇后休息了24分钟,再同时继续行驶,设两车之间的距离为y(km),货车行驶时间为x(h),请结合图像信息解答下列问题:(1)货车的速度为_km/h,轿车的速度为_km/h;(2)求y与x之间的函数关系式(写出x的取值范围),并把函数图像画完整;(3)货车出发_h,与轿车相距30km-参考答案-一、单选题1、D【解析】【分析】先判断 再利用待定系数法求解各选项对应的一次函数的解析式,即可得到答案.【详解】解: 一次函数,其中y的值随x值的增大而减小, 当时,则 解得,故A不符合题意,当时,则 解得 故B不符合题意;当时,则 解得 故C不符合题意;当时,则 解得 故D符合题意;故选D【点睛】本题考查的是一次函数的性质,利用待定系数法求解一次函数的解析式,掌握“利用待定系数法求解一次函数的解析式”是解本题的关键.2、A【解析】略3、B【解析】【分析】根据直线ykxb经过一、二、四象限,可得k0,b0,从而得到直线ybxk过一、二、三象限,即可求解【详解】解:直线ykxb经过一、二、四象限,k0,b0,k0,直线ybxk过一、二、三象限,选项B中图象符合题意故选:B【点睛】本题主要考查了一次函数的图象和性质,熟练掌握一次函数的图象和性质是解题的关键4、B【解析】【分析】根据菜园的三边的和为24m,进而得出一个x与y的关系式,然后根据题意可得关于x的不等式,求解即可确定x的取值范围【详解】解:根据题意得,菜园三边长度的和为24m,即,所以,由y0得,解得,当时,即,解得,故选:B【点睛】题目主要考查一次函数的运用及根据条件得出不等式求解,理解题意,利用不等式得出自变量的取值范围是解题关键5、D【解析】【分析】根据两个解析式中一次项系数的符号相反、常数项的符号相反,结合一次函数的图象与性质即可解决【详解】根据直线和的解析式知,k与2k、符号相反,b与b符号相反(由图知b0);A选项中的直线与y轴的交点均在y轴正半轴上,故不合题意;B、C两选项中两直线从左往右均是上升的,则k与2k全为正,也不合题意;D选项中两直线满足题意;故选:D【点睛】本题考查了一次函数的图象与性质,掌握一次函数的图象与性质,数形结合是关键本题的关键6、C【解析】【分析】根据函数图象中的数据,可以分别计算出两人的速度,从而可以判断各个选项中的说法是否正确,从而可以解答本题【详解】解:由图象可知,两人出发1小时后相遇,故选项A正确;王明跑步的速度为243=8(km/h),故选项B正确;陈启浩的速度为:241-8=16(km/h),陈启浩从开始到到达目的地用的、时间为:2416=1.5(h),故陈启浩到达目的地时两人相距81.5=12(km),故选项C错误;陈启浩比王提前3-1.5=1.5h到目的地,故选项D正确;故选:C【点睛】本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答7、C【解析】【分析】求出正比函数的解析式,k值的绝对值表示车的速度;横轴上两个时间点的差表示乙走完全程所用时间,求出一次函数的解析式,确定它与正比例函数的交点坐标,横坐标即为二车相遇时间【详解】设甲的解析式为y=kx,6k=300,解得k=50,=50 x,甲车的速度为,正确;乙晚出发2小时,乙车用了5-2=3(h)到达城,错误;设,即甲行驶4小时,乙
下列哪些考试行为属于考生违纪:()
- A、考生未经监考员同意,在考试过程中擅自离开考场。
- B、考生将试卷、答题卡、草稿纸等考试用纸带出考场。
- C、考生用规定以外的笔或者纸答题,或者在答题卡规定以外的地方书写姓名、准考证号。
- D、考生在答题卡上填写与本人身份不符的姓名和准考证号等信息。
正确答案:A,B,C
“请考生注意,未将试题答案填涂在答题卡上的,请抓紧时间填涂”监考规范用语提示时间为()
- A、考试结束前30分钟
- B、考试结束前15分钟
- C、开考后30分钟
- D、开考后15分钟
正确答案:B
监考员处理缺考考生试卷、答题卡及空白试卷、答题卡操作为()。
- A、将缺考考生的条形码粘贴在《考场情况记录表》上规定区域内
- B、用0.7黑色墨水的签字笔在答题卡袋封面上填缺考准考证号及相关内容
- C、用0.7黑色墨水的签字笔在缺考答题卡上填写缺考考生姓名和准考证号
- D、用0.7黑色墨水的签字笔在《考场情况记录表》上规定区域填写缺考考生姓名和准考证号
- E、用0.7黑色墨水的签字笔分别在缺考考生试卷、答题卡和尾考场的空白试卷、空白答题卡左上角空白处注明“缺考”或“空白”字样
- F、用2B铅笔填涂缺考考生答题卡的缺考标记
正确答案:A,B,C,E
关于考生考试规范作答,说法正确的是()
- A、选择题部分用2B铅笔填涂答案,考生按填涂示例涂满、涂黑。非选择题部分用0.5毫米黑色墨水的签字笔作答。作图须用2B铅笔绘、写清楚,线条及符号等须加黑、加粗
- B、答题区域:根据考试的有关规定和网上评卷答题的有关要求,考生必须在规定区域答题
- C、答题语言:笔试一律用国家通用语言文字答卷,否则答题无效
- D、D、作答选做题:在作答选做题时,答题卡上预留了B两道选做题的答题区域,以考生在相应区域内实际作答的内容为准评卷。如考生A、B两题均做,评卷时以A题为准进行判分
正确答案:A,B,C,D
考试结束后,主考和监考应完成哪些工作,才能允许考生离场()。
- A、填写完“考场记录表”
- B、检查试卷答卷有无破损、缺失
- C、将考试资料清点整理后送交总监考
- D、将试卷答卷及其它回收资料清点计数
- E、将答题卡按照考生序号由小到大排列,放入“答题卡返回袋”内
正确答案:B,D
