2021年浙江省舟山市中考数学试卷答案解析(Word版本)
选答型试题要求学生从教师提供的若干答案中挑选出正确的答案,可以分为是非题、多项选择题与____三种。
组配式试题
选答型试题要求学生从教师提供的若干答案中挑选出正确的答案,可以分为是非题、多项选择题与____________________三种。
组配式试题
一、单项选择题(共60题,每题0.5分,共30分.以下备选答案中只有一项最符合题目要求,不选、错选均不得分)
1.内部控制的实质是( ).
A.控制信息
B.合理评价和控制风险
C.监督财务
D.控制内部活动
1.B【解析】证券公司或基金公司的内部控制是指通过分析财务及评价手段来控制投资风险,以避免投资风险过大。
将word文档中的表格复制到当前Excel工作表中。 解析:本题主要考核“导入Word表格”这个考点。
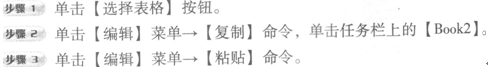
浙江省舟山市定海区司法考试的考点一般在哪里?
这个我不清楚,你可以咨询当地司法局。
/19 /192021年浙江省舟山市中考数学试卷答案解析(Word版本)2021年浙江省舟山市中考数学试卷答案解析(Word版本)一、选择题(本题有10小题,每题3分,共30分。请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1(3分)下列几何体中,俯视图为三角形的是()ABCD2(3分)2021年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km,数1500000用科学记数法表示为()A.15X105B.1.5X106C.0.15X107D.1.5X105(3分)2021年14月我国新能源乘用车的月销量情况如图所示,贝V下列说法错误的是()1月份销量为2.2万辆从2月到3月的月销量增长最快C.4月份销量比3月份增加了1万辆D.14月新能源乘用车销量逐月增加(3分)不等式1-x2的解在数轴上表示正确的是()A.D.B.C.(3分)将一张正方形纸片按如图步骤,沿虚线对折两次,然后沿中平行于底边的虚线剪去一个角,展开铺平后的图形是()A.B.C.D.6(3分)用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A.点在圆内点在圆上点在圆心上D.点在圆上或圆内(3分)欧几里得的原本记载,形如x2+ax=b2的方程的图解法是:画RtAABC,使ZACB=90,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是()A.AC的长B.AD的长C.BC的长D.CD的长(3分)用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是()A.B.C.D.(3分)如图,点C在反比例函数y=(x0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,AOB的面积为1,则k的值为()A.1B.2C.3D.4(3分)某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是()A.甲B.甲与丁C.丙D.丙与丁二、填空题(本题有6小题,每题4分,共24分)11.(4分)分解因式:m2-3m=.12.(4分)如图,直线111213,直线AC交11,12,13于点A,B,C;直线DF交11,12,13于点D,E,F,已知=,则13(4分)小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我嬴”小红赢的概率是,据此判断该游戏(填“公平”或“不公平”)(4分)如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60,则该直尺的宽度为cm.(4分)甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少10%,若设甲每小时检测x个,则根据题意,可列出方程:.(4分)如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作RtAEFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.三、解答题(本题有8小题,第1719题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)17.(6分)(1)计算:2(2)化简并求值()?-1)+|-3|-(-1)0;,其中a=1,b=2.时,两位同学的解法如下:(6分)用消元法解方程组解法一:由-,得3x=3.解法二:由得,3x+(x-3y)=2,把代入,得3x+5=2.(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“X“.(2)请选择一种你喜欢的方法,完成解答.(6分)已知:在厶ABC中,AB=AC,D为AC的中点,DE丄AB,DF丄BC,垂足分别为点E,F,且DE=DF.求证:AABC是等边三角形.(8分)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:收集数据(单位:mm)甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.整理数据:165.5170.521170.5175.542175.5180.55a180.5185.56b185.5190.522190.5195.510甲车间乙车间分析数据:车间甲车间乙车间应用数据:平均数180180众数185180中位数180180方差43.122.6(1)计算甲车间样品的合格率.(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.21.(8分)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.(1)根据函数的定义,请判断变量h是否为关于t的函数?(2)结合图象回答:当t=0.7s时,h的值是多少?并说明它的实际意义.秋千摆动第一个来回需多少时间?22.(10分)如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为PDE,F为PD的中点,AC=2.8m,PD=2m,CF=lm,ZDPE=20,当点P位于初始位置P0时,点D与C重合(图2).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.(1)上午10:00时,太阳光线与地面的夹角为65(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.lm)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离?(结果精确到0.1m)(参考数据:sin700.94,cos700.34,tan702.75,1.41,1.73)223.(10分)已知,点M为二次函数y=-(x-b)+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A、,B,且mx+5-(x-b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点皿在厶AOB内,若点C(,y1),D(,y2)都在二次函数图象上,试比较y1与y2的大小.24.(12分)我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.(1)概念理解:如图1,在厶ABC中,AC=6,BC=3,ZACB=30,试判断厶ABC是否是”等高底”三角形,请说明理由.(2)问题探究:如图2,ABC是“等高底”三角形,BC是”等底”,作AABC关于BC所在直线的对称图形得到ABC,连结AA交直线BC于点D.若点8、是厶AAC的重心,求的值.(3)应用拓展: /19 /19如图3,已知lll2,11与12之间的距离为2.“等高底”AABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的倍.将ABC绕点C按顺时针方向旋转45得到ABC,A,C所在直线交12于点D.求CD的值.2021年浙江省嘉兴市中考数学试卷参考答案与试题解析一、选择题(本题有10小题,每题3分,共30分。请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1(3分)下列几何体中,俯视图为三角形的是()ABCD【分析】根据从上边看得到的图形是俯视图,可得答案.【解答】解:A、俯视图是圆,故A不符合题意;B、俯视图是矩形,
二、多项选择题(每道试题下有A、B、C、D四个备选答案,其中有两个或两个以上的答案是正确的,请从中选择正确的答案,不选、错选、多选、少选均不得分。本类题共10道题,每题2分,共20分)
属于会计档案的有( )。
A.记账凭证汇总表
B.备查账
C.会计报表附注
D.银行对账单
【答案】ABCD
【考点】会计档案的理解
【解析】根据我国《会计档案管理办法》第5条的规定可知,A、B、C、D四项均属于会计档案。故选ABCD.
5、The Chinese people, in their drinking of tea, ____ much significance on the act of "savoring." 中国人饮茶,注重"品"。
attachholdplaceregard
attach
hold
place
regards
题目解析:正确答案: place
解释:答案:place
解析:place significance on注重;赋予……重要性。相当于attach significance to。
这题答案为什么不可以选 attach ???
He'll attach the label to your luggage.
他会把标签系在你的行李上。
This hospital is attached to the medical college nearby.
这个医院附属附近的那所医学院。
He attached himself to the expedition.
他参加了那个探险队。
How can you attach the blame for this accident to the taxi-driver?
你怎么能把这次事故的责任归于出租车司机呢?
The new employee was attached to the sales department.
新来的雇员被派在销售部工作。
不及物动词 vi.
The blame for this accident attaches to the man who drove under the influence.
这起事故的责任应由酒后开车的那个人承担。
Those are advantages that attach to the profession.
那些都是从事该职业的种种有利条件。
以下结果来自互联网网络释义
英语四级考试大纲词汇第一卷 第一章在线阅读...
attachvt.缚,系,贴;附加
我们所熟知的有一个词组是:attach importance to(重视)
我们所熟知的有一个词组是:attach importance to(重视)
数理能力部分包括两种类型的题目,均为单项选择题。每小题给出的四个选项中。只有一项是符合题意的。请将正确选项选出。不选或错选,该题均不得分。
一、数学应用(56--65题):每道试题中给出表述数字关系的一段文字材料,要求考生通过分析、判断、运算。从四个选项中找出最符合题意的答案。
请开始答题:
56.若x,Y,z是三个连续的负整数,并且x>y>z,则下列表达式是正奇数的是( )。
A.yz—x
B.(x—y)(y--z)
C.x—yz
D.x(y+z)
56.B [解析]X、y、Z是三个连续的负整数,并且x>y>z,所以x—Y= Y- z=1,得到(x—y)(y—z)=1,选择B。
B. 每题只能选一个答案
C. 尽量不选择中性答案
D. 先分效度量表结果
16PF测验结构明确,每一题都备有三个可能的答案,被试可任选其一。在两个相反的选择答案之间有一个折中的或中性的答案,使被试有折中的选择(例题如,我喜欢看球赛:a.是的,b.偶然的,c.不是的;或如,我所喜欢的人大都是:a.拘谨缄默的, b.介于a与c之间的,c.善于交际的),避免了在是否之间必选其一的强迫性。所以被试答题的自发性和自由性较好。16PF需要告诫受测者尽量不选择中性答案。
B. 55
C. 60
D. 65
更多 “2021年浙江省舟山市中考数学试卷答案解析(Word版本)” 相关考题
相关内容
最新试卷
热门试卷
- 精品解析:2020年广东省广州市中考语文试题(原卷版)-20220726
- 精品解析:甘肃省白银市、武威市、张掖市、平凉市、酒泉市、庆阳市、陇南市、临夏州2020年中考语文试题(原卷版)-20220726
- 知到网课答案有机化学下华东理工大学版满分考试答案.docx-
- 精品解析:广西北部湾经济区2020年初中学业水平考试语文试题(解析版)
- 精品解析:广西北部湾经济区2020年初中学业水平考试语文试题(原卷版)
- 精品解析:贵州省黔东南2020年中考语文试题(解析版)
- 精品解析:贵州省黔西南州2020年中考语文试题(解析版)
- 精品解析:河北省2020年中考语文试题(解析版)-20220726
- 知到网课答案高等数学经管类上海财经大学版满分考试答案.docx-
- 2020年课标版高考语文押题精粹试卷及答案-10-
