设X=－0.1010,Y=－0.0100,则用原码定点加法求X＋Y的和为()A、0.0010B、1.0010C、0.1110D、1.1110

题目
设X=－0.1010,Y=－0.0100,则用原码定点加法求X＋Y的和为()

A、0.0010

B、1.0010

C、0.1110

D、1.1110

相似考题

1.运算中会产生溢出的是()A、X=0.1011Y=-0.1111求[X+Y]补B、X=0.1010Y=-0.0110求[X+Y]补C、X=0.1011Y=-0.1101求[X-Y]补D、X=0.1010Y=-0.0010求[X-Y]补

2.设随机变量(X,Y)的联合密度函数为f(x,y)=(1)求P(X>2Y)；(2)设Z=X+Y,求Z的概率密度函数.

3.设随机变量X～E(λ),令Y=,求P(X+Y=0)及FFY(y).

4.设X=－0.1010,Y=－0.0100,则用补码定点加法求X＋Y的和为()A、0.0010B、1.0010C、0.1110D、1.1110

更多“设X=－0.1010,Y=－0.0100,则用原码定点加法求X＋Y的和为() ”相关问题

  • 第1题：

    设随机变量X,Y相互独立，且X的概率分布为P{X=0)=P{X=2)=，Y的概率密度为
    　　(Ⅰ)求P{Y≤EY}；
    　　(Ⅱ)求Z=X+Y的概率密度.


    答案：
    解析：

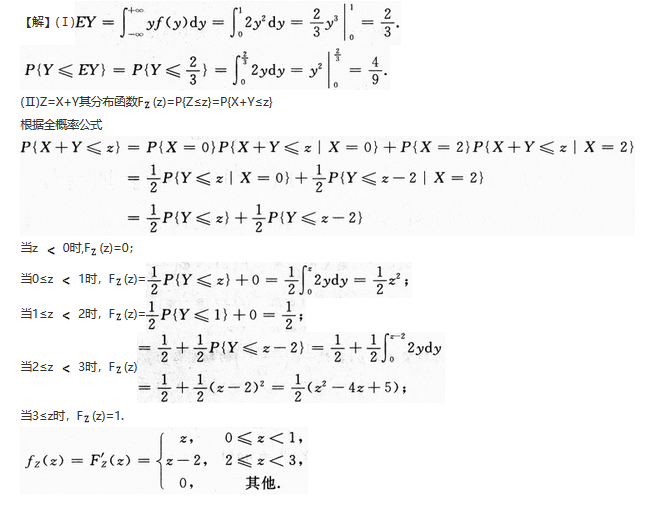
  • 第2题：

    已知x=-0.01111，y=+0.11001,求：x+y，结果用原码表示，若溢出，则填“溢出“


    [x]原=1001111[x]补=1110001[-x]补=0001111[y]原=0011001[y]补=0011001[-y]补=1100111[x+y]补=0001010x-y转换为加法：[x-y]补＝[x]补+[-y]补=1011000均无溢出x+y=10,x-y=-40

  • 第3题：

    已知 X= - 0.1010 ，Y=0.1101, 用原码一位除法计算[X/Y]原=？


    01011;1110;00000;0;01011;1111

  • 第4题：

    设Y=y((x)满足2y+sin(x+y)=0，求y′．


    答案：
    解析：
    将2y+sin(x+y)=0两边对x求导，得

  • 第5题：

    设X与Y独立同分布,共同分布为N（0,1), 求概率P（X+Y|≤|X-Y|).


    所以 又因Y i ～N(0，9)，故 且Y 1 ，…，Y 9 相互独立，得 又因 相互独立，故 处理 的原则是：“先标准化再平方”，而处理 的方法是：“先加起来再标准化”，这是因为正态分布有线性变换下仍为正态分布这一好性质，而数理统计的几个特殊分布( 、t、F分布)都是建立在N(0，1)的基础之上．中间的两次“独立性”勿忘了说，因为 、t、F分布的构成中都有“独立性”的要求，请勿忽视．

相关内容