有关等差系列年值，理解正确的有()A、在i和n既定的情况下，已知初始值A1，等差额G，就可以求得等额系列年值A0，即每年年末需支付的等额资金B、在i和n既定的情况下，已知初始值A1，等差额G，就可以求得等额系列年值A0，由A0+A1可以得出每年年末应等额支付资金C、在i和n既定的情况下，已知初始值A1，等差额G，由现值P求A0和由终值F求A0的结果相同D、在i和n既定的情况下，已知初始值A1，等差额G，由现值P求A0和由终值F求A0的结果不同E、利用等差系列年值公式，可以把等差系列通过等值的概念转换成等额

题目

有关等差系列年值，理解正确的有()

A、在i和n既定的情况下，已知初始值A1，等差额G，就可以求得等额系列年值A0，即每年年末需支付的等额资金

B、在i和n既定的情况下，已知初始值A1，等差额G，就可以求得等额系列年值A0，由A0+A1可以得出每年年末应等额支付资金

C、在i和n既定的情况下，已知初始值A1，等差额G，由现值P求A0和由终值F求A0的结果相同

D、在i和n既定的情况下，已知初始值A1，等差额G，由现值P求A0和由终值F求A0的结果不同

E、利用等差系列年值公式，可以把等差系列通过等值的概念转换成等额系列

相似考题

1.已知等差数列{an}的首项与公差相等，{an）的前n项的和记作Sn，且S20=840．（I）求数列{an}的首项a1及通项公式；（Ⅱ）数列{an}的前多少项的和等于847.

2.有关等额分付资本回收公式理解正确的是()A、在经济系统开始时，一次存入多少钱，才能在以后n个周期内连续每期期末取出A，最后正好全部取完B、在回收周期数n既定情况下，求每期期末取出的资金为多少时，才能在第n期末把全部本利取出C、在n既定情况下，求分期等额存入值为多少时，才能与第n期的终值F相等D、在n期既定时，每一个计息周期期末均支付相同的数额A，求相当于n年后一次支付的终值为多少

3.在等差数列{an}中，已知a1=2，且a2+a4=20，若an=18，则n=5。()

4.在资金等值计算的基本公式中，等额支付系列年金现值公式的系数可以表示成()A. (P/A，i，n)B. (P/F，i，n)C. (A/P，i，n)D. (F/A，i，n)

更多“有关等差系列年值,理解正确的有()A、在i和n既定的情况下,已知初始值A1,等差额G,就可以求得等额 ”相关问题

  • 第1题：

    已知一等差数列a1，21，a3，31，…，an，…，若an=516，则该数列前n项的平均数是（ ）

    A．266 B．258 C．255 D．212

    答案：A
    解析：
    由等差数列的第2项和第4项可求出其公差d==5，则首项a1=21-5=16。又已知an=516，根据等差数列求和公式Sn==平均数×n，可得前n项的平均数为=266。

  • 第2题：

    等额系列偿债基金系数(A／F，i，n)的计算式是(　　)。


    答案：B
    解析：
    参考第四章第一节内容，应选B项。 区分：
    (1)等额系列终值系数(或年金终值系数)，等额系列现值系数(或年金现值)。
    (2)等额系列资金回收系数，等额系列偿债基金系数。

  • 第3题：

    在等差数列{an)中，已知a1=2，且a2+a4=20，若an=18，则n=5。 ( )


    答案：对
    解析：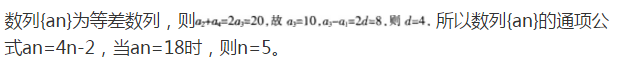

  • 第4题：

    等额支付系列（年金）现值系数的数学表示方式为：（ ）．

    A、（A/F,i，n）
    B、（A/P,i，n）
    C、（F/A,i，n）
    D、（P/A,i，n）

    答案：D
    解析：
    2020/2019版教材P9
    考点:现金现值系数，等额支付系列现值系数或年金现值系数，用符号﹙P／A，i，n）表示,

  • 第5题：

    折算值按时间点分类不包括( )。

    A.初始值
    B.现值
    C.等额年值
    D.终值

    答案：A
    解析：
    折算值是指把资金流量按一定折算率折算到某一时间点上的数值，按时间点不同可分为现值、终值和等额年值三种。

相关内容