无向图G=(V，E)，其中V={a，b，c，d，e，f}，E={(a，b)，(a，e)，(a，c)，(b，e)，(c，f)，(e，d)}，对该图进行深度优先遍历，得到的顶点序列正确的是()。A.a，b，e，c，d，f B.a，c，f，e，b，d C.a，e，b，c，f，d D.a，e，d，f，c，b

题目
无向图G=(V，E)，其中V={a，b，c，d，e，f}，E={(a，b)，(a，e)，(a，c)，(b，e)，(c，f)，(e，d)}，对该图进行深度优先遍历，得到的顶点序列正确的是()。

A.a，b，e，c，d，f
B.a，c，f，e，b，d
C.a，e，b，c，f，d
D.a，e，d，f，c，b
相似考题

1.设一个图G={V,{A}},V={a,b,c,d,e,f},A={,,,,,,}。那么顶点e的入度是_____;出度是_____;通过顶点f的简单回路有_____条;就连通性而言,该图是_____图;它的强连通分量有_____个;其生成树可能的最大深度是_____。

2.设D=V,E为有向图,V={a,b,c,d,e,f},E={a,b,b,c,a,d,d,e,f,e}是()。A、强连通图B、单向连通图C、弱连通图D、不连通图

3.已知一个图如图1.1所示，从顶点b出发进行广度优先遍历可能得到的序列为(23)。A．b a c e d fB．b a c d f eC．b a c e f dD．b a c e f d

4.设连通图G中的边集E={(a,b),(a,e),(a,c),(a,e),(b,d),(d,f),(f,c)),则从顶点a出发可以得到一种深度优先遍历的顶点序列为()。A.不能延伸网络可操作的距离B.不能过滤网络流量C.不能在网络上发送变弱的信号D.不能放大变弱的信号

更多“无向图G=(V，E)，其中V={a，b，c，d，e，f}，E={(a，b)，(a，e)，(a，c)，(b，e)，(c，f)，(e，d)}，对该图进行深度优先遍历，得到的顶点序列正确的是()。”相关问题

  • 第1题：

    对图分别进行深度优先遍历和广度优先遍历,得到的顶点访问序列________。

    A、一定相同

    B、一定不同

    C、不一定相同

    D、可能相同


    参考答案：CD

  • 第2题：

    ● 对连通图进行遍历前设置所有顶点的访问标志为 false（未被访问） ，遍历图后得到一个遍历序列，初始状态为空。深度优先遍历的含义是：从图中某个未被访问的顶点 v 出发开始遍历，先访问 v 并设置其访问标志为 true（已访问） ，同时将 v 加入遍历序列，再从 v 的未被访问的邻接顶点中选一个顶点，进行深度优先遍历；若 v的所有邻接点都已访问，则回到 v 在遍历序列的直接前驱顶点，再进行深度优先遍历，直至图中所有顶点被访问过。 （40） 是下图的深度优先遍历序列。

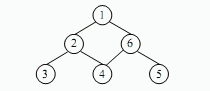
    （40）

    A. 1 2 3 4 6 5

    B. 1 2 6 3 4 5

    C. 1 6 2 5 4 3

    D. 1 2 3 4 5 6


    正确答案：A

  • 第3题：

    以下关于图的遍历的叙述中，正确的是(61)。

    A.图的遍历是从给定的源点出发对每一个顶点仅访问一次的过程

    B.图的深度优先遍历方法不适用于无向图

    C.使用队列对图进行广度优先遍历

    D.图中有回路时则无法进行遍历


    正确答案：C

  • 第4题：

    已知图G＝(V,E)，其中V＝(a，b，c，d，e，f)，E：{＜a，b＞，＜a，d＞，＜a，e＞，＜d，e＞，＜e， b＞，＜c，b＞，＜c，e＞，＜c，b，＜f，e＞}，则从该图的顶点a出发的深度优先遍历序列是(51)，广度优先遍历序列是(52)，其深度优先生成树(或森林)是(53)，广度优先生成树(或森林)是(54)，该图的一个拓扑序列是(55)。

    A．abdecf

    B．abdcef

    C．aebdcf

    D．adebfe


    正确答案：A
    解析：图的深度优先遍历是从图中的某个节点V1出发，访问此节点，然后依次从V1的未被访问的邻接点进行深度优先遍历，直到图中所有和V1有路径相通的节点都被访问到。若此时图中尚有节点未被访问，则选图中的一个未被访问的接点作起点。重复此过程。因此此图的深度优先遍历序列是abcdef。广度优先遍历是先访问结点V1，然后访问V1连接到的所有未被访问的结点V2，V3，，…Vt，再依次访问V2，V3，…，Vt连接到的所有未被访问的结点。如此进行下去，直到访问遍所有结点。冈此，此图的广度优先遍历序列是abdecf。对于连通图，从图的任一顶点出发进行深度优先遍历时，所经过的边与连通图的所有顶点构成的生成树为图的深度优先生成树；从图的任一顶点山发进行广度优先遍历时，所经过的边与连通图的所有顶点构成的生成树为图的广度优先生成树。对于非连通图，图中的每一个连通分量的生成树的集合为生成森林：按深度优先遍历得到的为深度优先生成森林，按广度优先遍历得到的为广度优先生成森林。因此，图G的深度优先生成森林和广度优先生成森林分别为：如果有向图的某个结点序列满足如下条件：若从结点V1到vj有一条路径，则在序列中结点Vi必定在vj之前，则称该序列是一个拓扑序列。任何无环有向图的结点都可以排在一个拓扑序列中。拓扑排序的方法是重复执行下列步骤(1)和(2)，直到所有结点均已被输出。1．从图中选择一个入度为0的结点且输出。2．从图中删除此结点及其所有的出边。在可供选择的答案中，C是一个拓扑序列。

  • 第5题：

    图G的邻接矩阵如下图所示（顶点依次表示为v0、v1、v2、v3、v4、v5），G是（请作答此空）。对G进行广度优先遍历（从v0开始），可能的遍历序列为（ ）。


    A.无向图
    B.有向图
    C.完全图
    D.强连通图

    答案：B
    解析：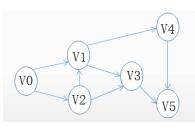

  • 第6题：

    设连通图G中的边集E={（a，b），（a，e），（a，c），（b，e），（e，d），（d，f），（f，c）}，则从顶点a出发可以得到一种深度优先遍历的顶点序列为（）

    • A、abedfc
    • B、acfebd
    • C、aebdfc
    • D、aedfcb

    正确答案:B

  • 第7题：

    假定一个有向图的边集为{，，< c，f>，< d，c>，< e，b>，< e，d>}，对该图进行拓扑排序得到的顶点序列为（）


    正确答案:aebdcf

  • 第8题：

    无向图G=（V，E），其中V={a，b，c，d，e，f}，E={（a，b），（a，e），（a，c），（b，e），（c，f），（f，d），（e，d）}，对该图进行深度优先遍历，得到的顶点序列正确的是（）。

    • A、a，b，e，c，d，f
    • B、a，c，f，e，b，d
    • C、a，e，b，c，f，d
    • D、a，e，d，f，c，b

    正确答案:D

  • 第9题：

    单选题
    用深度优先遍历方法遍历一个有向无环图，并在深度优先遍历算法中按退栈次序打印出相应的顶点，则输出的顶点序列是（）。
    A

    逆拓扑有序

    B

    拓扑有序

    C

    无序

    D

    深度优先遍历序列


    正确答案： B
    解析： 暂无解析

  • 第10题：

    填空题
    如果无向图G有n个顶点、e条边且用邻接矩阵进行存储，那么深度优先遍历图G的时间复杂度为（）。

    正确答案： O(N2)
    解析： 暂无解析

  • 第11题：

    单选题
    设连通图G中的边集E={（a，b），（a，e），（a，c），（a，e），（b，d），（d，f），（f，c）），则从顶点a出发可以得到一种深度优先遍历的顶点序列为（）。
    A

    abedfc

    B

    acfebd

    C

    abcedf

    D

    abcdef


    正确答案： A
    解析： 暂无解析

  • 第12题：

    填空题
    已知一无向图G=（V，E），其中V={a，b，c，d，e}E={（a，b），（a，d），（a，c），（d，c），（b，e）}现用某一种图遍历方法从顶点a开始遍历图，得到的序列为abecd，则采用的是（）方法。

    正确答案： 深度遍历
    解析： 暂无解析

  • 第13题：

    设无向图G中的边的集合E={(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c)},则从顶点a出发进行深度优先遍历可以得到的一种顶点序列为()。

    A.aedfcb

    B.acfebd

    C.aebcfd

    D.aedfbc


    正确答案：B

  • 第14题：

    设有向图G=(V，E)，其中V={V1，V2，V3，V4，V5，V6，V7，V8)，E={V1，V2＞，＜V1，V3＞，＜V2，V4＞，＜V2，V6＞，＜V3，V5＞，＜V4，V8＞，＜V5，V4＞，＜V6，V3＞，＜V6，V7＞， (V7，V5＞，＜V8，V7＞)，那么该图的邻接表可以是(10)，按照该邻接表从V1，出发，图G的深度优先遍历序列为(11)，广度优先遍历序列为(12)。

    A．

    B．

    C．

    D．


    正确答案：B

  • 第15题：

    阅读以下说明和代码，填补代码中的空缺，将解答填入答题纸的对应栏内。 【说明】 图是很多领域中的数据模型，遍历是图的一种基本运算。从图中某顶点v出发进行广度优先遍历的过程是： ①访问顶点v； ②访问V的所有未被访问的邻接顶点W1 ,W2 ,..,Wk； ③依次从这些邻接顶点W1 ,W2 ,..,Wk出发，访问其所有未被访问的邻接顶点；依此类推，直到图中所有访问过的顶点的邻接顶点都得到访问。 显然，上述过程可以访问到从顶点V出发且有路径可达的所有顶点。对于从v出发不可达的顶点u，可从顶点u出发再次重复以上过程,直到图中所有顶点都被访问到。 例如，对于图4-1所示的有向图G，从a出发进行广度优先遍历，访问顶点的一种顺序为a、b、c、e、f、d。设图G采用数组表示法（即用邻接矩阵arcs存储），元素arcs[i][j]定义如下：图4-1的邻接矩阵如图4-2所示，顶点a~f对应的编号依次为0~5.因此，访问顶点a的邻接顶点的顺序为b，c，e。 函数BFSTraverse(Graph G)利用队列实现图G的广度优先遍历。 相关的符号和类型定义如下： define MaxN 50 ／*图中最多顶点数*／ typedef int AdjMatrix[MaxN][MaxN]； typedef struct{ int vexnum, edgenum; ／*图中实际顶点数和边（弧）数*／ AdjMatrix arcs; ／*邻接矩阵*／ )Graph; typedef int QElemType； enum {ERROR=0;OK=1}; 代码中用到的队列运算的函数原型如表4-1所述，队列类型名为QUEUE。 表4-1 实现队列运算的函数原型及说明

    【代码】 int BFSTraverse(Graph G) {//对图G进行广度优先遍历，图采用邻接矩阵存储 unsigned char*visited； //visited[]用于存储图G中各顶点的访问标志，0表示未访问 int v, w, u; QUEUEQ Q; ∥申请存储顶点访问标志的空间，成功时将所申请空间初始化为0 visited=(char*)calloc(G.vexnum, sizeof(char)); If( （1） ) retum ERROR; （2） ； //初始化Q为空队列 for( v=0; v<G.vexnum; v++){ if(!visited[v]){ //从顶点v出发进行广度优先遍历 printf("%d”，v)； //访问顶点v并将其加入队列 visited[v]=1； （3） ； while(！isEmpty(Q)){ （4） ； //出队列并用u表示出队的元素 for(w=0;v<G.vexnum; w++){ if（G.arcs[u][w]!=0&& （5） ){ //w是u的邻接顶点且未访问过 printf("%d”, w)； //访问顶点w visited[w]=1； EnQueue(&Q, w); } } } } free(visited); return OK; )//BFSTraverse


    正确答案：1、visited==NULL
    2、InitQueue(&Q)
    3、EnQueue(&Q,v)
    4、DeQueue(&Q,&u)
    5、visited==0

  • 第16题：

    已知有向图G=(V，A)，其中V={a，b，C，d，e}，A={＜a，b＞，＜a，c＞，＜d，c＞，＜d，e＞，＜b，e＞，＜c，e＞}，对该图进行拓扑排序，下面序列中()不是拓扑排序

    A.a，d，c，b，e
    B.d，a，b，c，e
    C.a，b，d，c，e
    D.a，b，c，d，e

    答案：D
    解析：

  • 第17题：

    若已知有向图G=（V，E），其中，顶点的集合为V={v1，v2，v3，v4，v5}，弧的集合为E={， ，，，，}，则G的拓扑序列有哪些？（写出结论即可）


    正确答案:G的拓扑序列有3个，分别是v1,v2,v3,v4,v5；v1,v3,v2,v4,v5和v1,v3,v4,v2,v5。

  • 第18题：

    如果无向图G有n个顶点、e条边且用邻接矩阵进行存储，那么深度优先遍历图G的时间复杂度为（）。


    正确答案: O(N2)

  • 第19题：

    已知一无向图G=（V，E），其中V={a，b，c，d，e}E={（a，b），（a，d），（a，c），（d，c），（b，e）}现用某一种图遍历方法从顶点a开始遍历图，得到的序列为abecd，则采用的是（）方法。


    正确答案:深度遍历

  • 第20题：

    用深度优先遍历方法遍历一个有向无环图，并在深度优先遍历算法中按退栈次序打印出相应的顶点，则输出的顶点序列是（）。

    • A、逆拓扑有序
    • B、拓扑有序
    • C、无序
    • D、深度优先遍历序列

    正确答案:A

  • 第21题：

    问答题
    若已知有向图G=（V，E），其中，顶点的集合为V={v1，v2，v3，v4，v5}，弧的集合为E={， ，，，，}，则G的拓扑序列有哪些？（写出结论即可）

    正确答案： G的拓扑序列有3个，分别是v1,v2,v3,v4,v5；v1,v3,v2,v4,v5和v1,v3,v4,v2,v5。
    解析： 暂无解析

  • 第22题：

    单选题
    无向图G＝（V，A），其中V＝｛a，b，c，d，e｝， A={，，＜d，c＞，＜d，e＞，＜b，e＞，＜c，e＞} 对该图进行扑拓排序，下面序列中（）不是拓扑序列。
    A

    adcbe

    B

    dabce

    C

    abdce

    D

    abcde


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    无向图G=（V，E），其中：V={a，b，c，d，e，f，E={（a，b）,（a,e）（a,c）,（b,e）,（c,f）,（f,d）,（e,d）}，对该图进行深度优先遍历，得到的顶点序列正确的是（  ）。
    A

    a,b,e,c,d,f

    B

    a,c,f,e,b,d

    C

    a,e,b,c,f,d

    D

    a,e,d,f,c,b


    正确答案： C
    解析：

相关内容