如果一棵二叉树结点的先根遍历序列是A、B、C，后根遍历序列是C、B、A，则该二叉树结点的中根遍历序列()。A.必为A、B、C B.必为A、C、B C.必为B、C、A D.不能确定

题目
如果一棵二叉树结点的先根遍历序列是A、B、C，后根遍历序列是C、B、A，则该二叉树结点的中根遍历序列()。

A.必为A、B、C
B.必为A、C、B
C.必为B、C、A
D.不能确定
相似考题

1.某二叉树的先根遍历序列和后根遍历序列相同,则该二叉树的特征是()。A.高度等于其结点数B.任一结点无左孩子C.任一结点无右孩子D.空或只有一个结点

2.树的基本遍历策略可分为先根遍历和后根遍历；二叉树的基本遍历策略可分为先序遍历、中序遍历和后序遍历。这里，我们把由树转换得到的二叉树叫做这棵树对应的二叉树。结论(27)是正确的。A．树的先根遍历序列与其对应的二叉树的先序遍历序列相同B．树的后根遍历序列与其对应的二叉树的后序遍历序列相同C．树的先根遍历序列与其对应的二叉树的中序遍历序列相同D．以上都不对

3.二叉树的先根遍历序列中，除根结点外，任一结点均处在其双亲结点的__________．

4.● 已知一个二叉树的先序遍历序列为①、②、③、④、⑤，中序遍历序列为②、①、④、③、⑤，则该二叉树的后序遍历序列为 （57） 。对于任意一棵二叉树，叙述错误的是 （58） 。（57）A. ②、③、①、⑤、④B. ①、②、③、④、⑤C. ②、④、⑤、③、①D. ④、⑤、③、②、①（58）A. 由其后序遍历序列和中序遍历序列可以构造该二叉树的先序遍历序列B. 由其先序遍历序列和后序遍历序列可以构造该二叉树的中序遍历序列C. 由其层序遍历序列和中序遍历序列可以构造该二叉树的先序遍历序列D. 由其层序遍历序列和中序遍历序列不能构造该二叉树的后序遍历序列

更多“如果一棵二叉树结点的先根遍历序列是A、B、C，后根遍历序列是C、B、A，则该二叉树结点的中根遍历序列()。”相关问题

  • 第1题：

    一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足()。

    A.所有的结点均无左孩子

    B、所有的结点均无右孩子

    C.只有一个叶子结点

    D、是任意一棵二叉树


    参考答案：C
    解释：因为先序遍历结果是“中左右”，后序遍历结果是“左右中”，当没有左子树时，就是“中右”和“右中”;当没有右子树时，就是“中左”和“左中”。则所有的结点均无左孩子或所有的结点均无右孩子均可，所以A、B不能选，又所有的结点均无左孩子与所有的结点均无右孩子时，均只有一个叶子结点，故选C。

  • 第2题：

    已知一棵二叉树结点的先根序列为ABDGCFK，中根序列为DGBAFCK，则结点的后根序列为________。

    A．ACFKBDG

    B．GDBFKCA

    C．KCFAGDB

    D．ABCDFKG


    正确答案：B
    解析：由这个二叉树的先根序列为ABDGCFK，中根序列为DGBAFCK，可知这棵二叉树的结构如下：故其后根序列应该是：

  • 第3题：

    已知一棵二叉树的先根序列为ABDGCFK，中根序列为DGBAFCK，则结点的后根序列为（ ）。


    正确答案：B
    通过两种树的遍历序列来推断第三种树的遍历时，反复利用前序和中序遍历的性质，就可以确定二叉树，具体：前序遍历的第一个结点A为树的根结点。中序遍历中A左边的结点在A的左子树中，A的右边的结点在A的右子树中。再分别对A的左右子树进行前面步骤重复处理，直到每个结点都找到正确的位置。

  • 第4题：

    一棵二叉树的前根遍历、后根遍历和中根遍历所产生的序列中，所有叶结点的先后顺序是 ( ) 。

    A．不相同

    B．完全相同

    C．前根遍历与后根遍历相同

    D．后根遍历与中根遍历相同


    正确答案：B
    解析：对二叉树的前根、后根、中根遍历，在遍历右子树的叶子结点前一定会先遍历左子树的叶子结点，因此叶子结点的顺序始终是一样的。

  • 第5题：

    对搜索二叉树进行(26)，得到的结点序列是升序序列。

    A．先序遍历

    B．中序遍历

    C．后序遍历

    D．层次遍历


    正确答案：B
    解析：中序遍历是先访问当前节点的左子树，在访问当前节点，最后防问右子树对搜索二叉树进行中序遍历，得到的结点序列是升序序列

  • 第6题：

    某二叉树的先序遍历(根、左、右)序列为 EFHIGJK 、中序遍历(左、根、右)序列为HFIEJKG, 则该二叉树根结点的左孩子结点和右孩子结点分别是（ ）。

    A.A,I.KB.F,IC.F,GD.I,G


    正确答案：C

  • 第7题：

    某二叉树的先序遍历(根、左、右)序列为 EFHIGJK 、中序遍历(左、根、右)序列为 HFIEJKG, 则该二叉树根结点的左孩子结点和右孩子结点分别是（37）

    A.A,I.K
    B. F,I
    C. F,G
    D.I,G

    答案：C
    解析：
    由先序遍历看，E为根节点，F为根节点的作孩子。在看中序遍历，则左树有：IE两个子结点。那么E的右孩子结点为G。

  • 第8题：

    若一个叶子结点是某二叉树的中序遍历序列的最后一个结点，则它必是该二叉树的先序遍历序列中的最后一个结点。()


    答案：对
    解析：
    二叉树的中序遍历是左子树、根结点、右子树，先序遍历的顺序是根结点、左子树、右子树，这两种遍历最后遍历的都是右子树，所以，中序遍历的最后一个结点必是先序遍历的最后一个结点。

  • 第9题：

    若一棵二叉树中的结点均无右孩子，则该二叉树的中根遍历和后根遍历序列正好相同。


    正确答案:正确

  • 第10题：

    判断题
    若一棵二叉树中的结点均无右孩子，则该二叉树的中根遍历和后根遍历序列正好相同。（  ）
    A

    对

    B

    错


    正确答案： 对
    解析：

  • 第11题：

    单选题
    某二叉树的先根遍历序列和后根遍历序列正好相反，则该二叉树具有的特征是（）。
    A

    高度等于其结点数

    B

    任一结点无左孩子

    C

    任一结点无右孩子

    D

    空或只有一个结点


    正确答案： D
    解析： 任一结点都无左孩子或任一结点都无右孩子

  • 第12题：

    判断题
    若一棵二又树中的结点均无右孩子，则该二又树的中根遍历和后根遍历序列正好相反。（  ）
    A

    对

    B

    错


    正确答案： 对
    解析：

  • 第13题：

    如果二叉树T2是由一棵树T1转换而来的二叉树,那么T1中结点的先根序列对应T2的()序列。

    A.先序遍历

    B.中序遍历

    C.后序遍历

    D.层次遍历


    参考答案：A

  • 第14题：

    某二叉树的先根遍历序列为CEDBA，中根遍历序列为DEBAC，则其后根遍历序列为【 】。


    正确答案：DADEC
    DADEC

  • 第15题：

    已知一棵二叉树的先根序列为ABCDEFK,中根序列为DGBAFCK,则结点的后根序列为( )。 A.ACFKDBGSX

    已知一棵二叉树的先根序列为ABCDEFK，中根序列为DGBAFCK，则结点的后根序列为（ ）。

    A.ACFKDBG

    B.GDBFKCA

    C.KCFAGDB

    D.ABCDFKG


    正确答案：B
    暂无解析，请参考用户分享笔记

  • 第16题：

    若一棵二叉树结点的前序遍历序列是A、B、C，后序遍历序列是C、B、A，则该二叉树结点的中序遍历序列( )。

    A．必为A、B、C

    B．必为A、C、B

    C．必为B、C、A

    D．不能确定


    正确答案：D
    解析：对一棵二叉树结点的前序遍历序列是A、B、C，后序遍历序列是C、B、A可以确定该树的根结点为A，B结点是C结点的父结点，但不能确定B具体为A的左孩子或右孩子，也不能确定C为B的左孩子还是右孩子，因此不能确定中序遍历的顺序。

  • 第17题：

    已知某二叉树的后根遍历序列是DABEC，中根遍历序列是DEBAC，它的先根遍历序列是(32)。

    A．ACBED

    B．DEBAC

    C．DECAB

    D．CEDBA


    正确答案：D
    解析：根据后根序列和中根序列可以构造出如下的二叉树：

  • 第18题：

    某二叉树为单枝树（即非叶子结点只有一个孩子结点）且具有n个结点（n>1）,则该二叉树（ ）


    A.共有n层，每层有一个结点
    B.共有log2n层，相邻两层的结点数正好相差一倍
    C.先序遍历序列与中序遍历序列相同
    D.后序遍历序列与中序遍历序列相同


    答案：A
    解析：
    若二叉树为单技树，那幺n个节点就分布在n层上。遍历序列则与遍历方法和二叉树的形态有关。例如，对于三个节点的单技二叉树，其形态可为：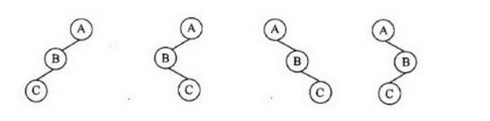

  • 第19题：

    一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反，则该二叉树一定满足()。

    A.所有的结点均无左孩子
    B.所有的结点均无右孩子
    C.只有一个叶子结点
    D.是任意一棵二叉树

    答案：C
    解析：
    先序遍历的次序为根一左一右，而后序遍历的次序为左一右一根，，先序遍历与后序遍历相对次序可以相反的部分为根一左(对后序的左一根)，或者是根一右(对后序的右一根)，所以满足条件的二叉树只有一个叶子结点。

  • 第20题：

    若二叉树的一个叶子结点是某子树中根遍历序列中的第一个结点，则它必然是该子树后根遍历序列中的（）个结点。


    正确答案:第一

  • 第21题：

    对平衡二叉树进行中根遍历，可得到结点的有序序列。


    正确答案:正确

  • 第22题：

    判断题
    若一个叶子结点是某二叉树的中序遍历序列的最后一个结点，则它必是该二叉树的先序遍历序列中的最后一个结点。(  )
    A

    对

    B

    错


    正确答案： 对
    解析：

  • 第23题：

    填空题
    若二叉树的一个叶子结点是某子树中根遍历序列中的第一个结点，则它必然是该子树后根遍历序列中的（）个结点。

    正确答案： 第一
    解析： 暂无解析

相关内容