在平衡二叉树中插入一个结点后造成了不平衡，设最低的不平衡结点为A，并已知A的左孩子的平衡因子为0，右孩子的平衡因子为1，则应作()型调整以使其平衡。A.LL B.LR C.RL D.RR

题目
在平衡二叉树中插入一个结点后造成了不平衡，设最低的不平衡结点为A，并已知A的左孩子的平衡因子为0，右孩子的平衡因子为1，则应作()型调整以使其平衡。

A.LL
B.LR
C.RL
D.RR
相似考题

1.在平衡二叉树中，(55)。A．任意结点的左、右子树结点数目相同B．任意结点的左、右子树高度相同C．任意结点的左、右子树高度之差的绝对值不大于1D．不存在度为1的结点

2.假设一棵平衡二叉树的每个结点都表明了平衡因子b,试设计一个算法,求平衡二叉树的高度。

3.在平衡二叉树中插入一个结点后造成了不平衡,设最低的不平衡结点为A,并已知A的左孩子的平衡因子为0右孩子的平衡因子为1,则应作()型调整以使其平衡。A.LLB、LRC、RLD、RR

4.下面关于哈夫曼树的叙述中，正确的是(58)。A．哈夫曼树一定是完全二叉树B．哈夫曼树一定是平衡二叉树C．哈夫曼树中权值最小的两个结点互为兄弟结点D．哈夫曼树中左孩子结点小于父结点、右孩子结点大于父结点

更多“在平衡二叉树中插入一个结点后造成了不平衡，设最低的不平衡结点为A，并已知A的左孩子的平衡因子为0，右孩子的平衡因子为1，则应作()型调整以使其平衡。”相关问题

  • 第1题：

    在平衡的二叉排序树中，向某个平衡因子不为零的结点的树中插入一新结点，必引起平衡旋转。()


    参考答案：错误

  • 第2题：

    由元素序列{27，16，75，38，51}构造平衡二叉树，则首次出现的最小不平衡子树的根(即离插入节点最近且平衡因子的绝对值为2的节点)为(9)。

    A．27

    B．38

    C．51

    D．75


    正确答案：D
    解析：二叉排序树的构造方法如下：每读入一个数据，建立一个新节点，若二叉排序树非空，则将新节点的值与根节点的值比较，。如果小于根节点的值，则插入到左子树中，否则插入到右子树中；若二叉排序树为空，则新节点作为二叉排序树的根节点。节点的平衡因子是指节点右子树深度与左子树深度之差。由数据{27，16，75，38，51}构造平衡二叉树，插入51后首次出现不平衡子树，易知最小不平衡子树的节点为75。

  • 第3题：

    由元素序列(27,16,75,38,51)构造平衡二叉树，则首次出现的最小不平衡子树的根(即离插入结点最近且平衡因子的绝对值为2的结点)为(46)。

    A．27

    B．38

    C．51

    D．75


    正确答案：D
    解析：平衡二叉树(AVL树)或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。二叉树结点的平衡因子(Balance　Factor,　BF)定义为该结点的左子树的深度减去其右子树的深度。平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。由元素序列(27,16,75,38,51)构造平衡二叉树的过程如下图所示，将元素51加入树中之前，二叉树保持平衡，加入结点51后，结点38的平衡因子由0变为-1，75所在结点的平衡因子由1变为2，27所在结点的平衡因子由-1变为-2。因此，75所在结点是离插入结点最近且平衡因子的绝对值为2的结点。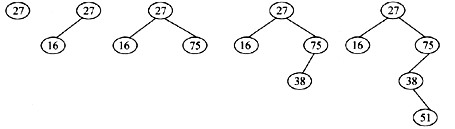

  • 第4题：

    对二叉树中的结点如下编号：树根结点编号为1，根的左孩子结点编号为2、右孩子结点编号为3，依此类推，对于编号为i的结点，其左孩子编号为2i、右孩子编号为2i+1。例如，下图所示二叉树中有6个结点，结点a、b、c、d、e、f的编号分别为1、2、3、5、7、11。那么，当结点数为n（n>0）的（ ）时，其最后一个结点编号为2i-1

    A.二叉树为满二叉树（即每层的结点数达到最大值）B.二叉树中每个内部结点都有两个孩子C.二叉树中每个内部结点都只有左孩子D.二叉树中每个内部结点都只有右孩子


    正确答案：C

  • 第5题：

    某二叉树如图所示，若进行顺序存储（即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1），则该数组的大小至少为（请作答此空）；若采用三叉链表存储该二叉树（各个结点包括结点的数据、父结点指针、左孩子指针、右孩子指针），则该链表的所有结点中空指针的数目为（ ）。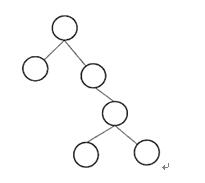

    A.6
    B.10
    C.12
    D.15

    答案：D
    解析：
    采用顺序存储结构存储二叉树时，一般的二叉树也必须按照完全二叉树的形式存储，需要填上一些不存在的"虚结点"。题中二叉树的高度为4，需要的存储空间为24-1=15，如下：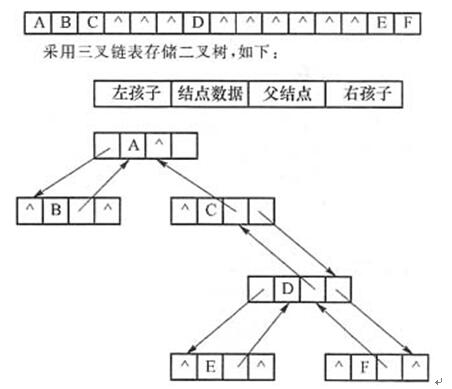

    可见，空指针的数目为8。

  • 第6题：

    在平衡二叉树中，向某个平衡因子不为零的结点的树中插入一新结点，必引起平衡旋转。


    正确答案:错误

  • 第7题：

    假定一棵二叉树顺序存储在一维数组a中，但让编号为1的结点存入a[0]元素中，让编号为2的结点存入a[1]元素中，其余类推，则编号为i结点的左孩子结点对应的存储位置为（），若编号为i结点的存储位置用j表示，则其左孩子结点对应的存储位置为（）。


    正确答案:2i-1；2j+1

  • 第8题：

    将树转换为二叉树的步骤如下： （1）加线。在所有（）结点之间加一条连线。 （2）去线。对树中每个结点，只保留它与第一个（）结点的连线，删除它与其他孩子结点之间的连线。 （3）层次调整。以树的根结点为轴心，为整棵树顺时针旋转一定的角度，使之结构层次分明。注意第一个孩子是二叉树结点的左孩子，兄弟转换过来的孩子是结点的右孩子。请完成填空（ ）。

    • A、兄弟；孩子
    • B、双亲；孩子
    • C、孩子；堂兄弟
    • D、兄弟；双亲

    正确答案:A

  • 第9题：

    一棵二叉树的广义表表示为a（b（c，d），e（f（，g））），则e结点的双亲结点为（），左孩子结点为（），右孩子结点为（）。


    正确答案:a；f；空结点（即无右孩子结点）

  • 第10题：

    填空题
    已知二叉树有50个叶子结点，且仅有一个孩子的结点数为30，则总结点数为（）。

    正确答案： 129
    解析： 暂无解析

  • 第11题：

    单选题
    在完全二叉树中，若一个结点是叶结点，则它没有（）。
    A

    左孩子结点

    B

    右孩子结点

    C

    左孩子和右孩子结点

    D

    左孩子结点，右孩子结点和兄弟结点


    正确答案： C
    解析： 暂无解析

  • 第12题：

    判断题
    在平衡二叉树中，向某个平衡因子不为零的结点的树中插入一新结点，必引起平衡旋转。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    在平衡二叉树中插入一个结点后引起了不平衡,设最低(最接近于叶子)的不平衡点是A,并已知A的左、右孩子的平衡因子分别为－1和0,则应进行的平衡旋转是()

    A.LL型

    B.LR型

    C.RL型

    D.RR型


    参考答案：B

  • 第14题：

    下图所示平衡二叉树(树中任一结点的左右子树高度之差不超过1)中，结点A的右子树AR高度为h，结点B的左子树BL高度为h，结点C的左子树CL、右子树CR高度都为h-1。若在CR中插入一个结点并使得CR的高度增加1，则该二叉树(61)。

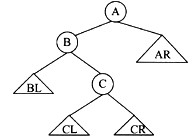
    A．以B为根的子二叉树变为不平衡

    B．以C为根的子二叉树变为不平衡

    C．以A为根的子二叉树变为不平衡

    D．仍然是平衡二叉树


    正确答案：C
    解析：本题考查平衡查找树。由于平衡二叉树中任一结点的左右子树高度之差不超过1，因此，若在CR中插入一个结点并使得CR的高度增加1，则结点C的左右子树高度之差为-1，同时以C为根的子树高度增加了1，所以结点B的左右子树高度之差变为-1。如此一来，A的左子树的高度为h+2、右子树的高度为h，根据定义，以A为根的子二叉树变为不平衡。

  • 第15题：

    平衡二叉树中任意结点的平衡因子只能是(50)之一。

    A．0，1，2

    B．0，1

    C．-1，+1

    D．0，-1，+1


    正确答案：D
    解析：平衡二叉树或者是一棵空树，或者是具有下列性质的二叉树：它的左子树都是平衡二叉树，且左右子树的深度之差的绝对值不超过1。平衡因子定义为该结点的左子树的深度减去其右子树的深度，所以平衡二叉树中任意结点的平衡因子只能是0、-1、+1之一。

  • 第16题：

    在平衡二叉树中插入一个结点后造成了不平衡，设最低的不平衡点为A，并已知A的左孩子的平衡因子为-1，右孩子的平衡因子为0，则做(14)型调整以使其平衡。

    A．LL

    B．LR

    C．RL

    D．RR


    正确答案：B
    解析：见平衡二叉树的调整。

  • 第17题：

    某二叉树如图所示，若进行顺序存储(即用一维数组元素存储该二叉树中的结点且通过下标反映结点间的关系，例如，对于下标为i的结点，其左孩子的下标为2i、右孩子的下标为2i+1)，则该数组的大小至少为（58）；若采用三叉链表存储该二叉树(各个结点包括结点的数据、父结点指针、左孩子指针、右孩子指针)，则该链表的所有结点中空指针的数目为（59）。

    A.6
    B.8
    C.12
    D.14

    答案：B
    解析：
    采用顺序存储结构存储二叉树时，一般的二叉树也必须按照完全二叉树的形式存储，需要填上一些不存在的“虚结点”。题中二叉树的高度为4，需要的存储空间为24-1=15，如下：可见，空指针的数目为8。

  • 第18题：

    已知二叉树有50个叶子结点，且仅有一个孩子的结点数为30，则总结点数为（）。


    正确答案:129

  • 第19题：

    在对二叉树进行顺序存储时，若下标为6的结点P既有双亲结点，又有左孩子结点和右孩子结点，则P的双亲结点的下标为（），左孩子结点的下标为（），右孩子结点的下标为（）


    正确答案:3；12；13

  • 第20题：

    在完全二叉树中，若一个结点是叶结点，则它没有（）。

    • A、左孩子结点
    • B、右孩子结点
    • C、左孩子和右孩子结点
    • D、左孩子结点，右孩子结点和兄弟结点

    正确答案:C

  • 第21题：

    对于一棵完全二叉树，设一个结点的编号为I，若它的左孩子结点存在，则其编号为（）；若右孩子结点存在，则其编号为（）；而双亲结点的编号为（）


    正确答案:2i；2i+1；[i/2]

  • 第22题：

    填空题
    一棵二叉树的广义表表示为a（b（c，d），e（f（，g））），则e结点的双亲结点为（），左孩子结点为（），右孩子结点为（）。

    正确答案： a,f,空结点（即无右孩子结点）
    解析： 暂无解析

  • 第23题：

    填空题
    在对二叉树进行顺序存储时，若下标为6的结点P既有双亲结点，又有左孩子结点和右孩子结点，则P的双亲结点的下标为（），左孩子结点的下标为（），右孩子结点的下标为（）

    正确答案： 3,12,13
    解析： 由二叉树的性质⑤可知，若对任一完全二叉树上的所有结点按层从左向右编号，则结点编号之间的数值关系可以准确地反映结点之间的逻辑关系。因此，对于完全二叉树的顺序存储来说，采用的是“以编号为地址”的策略将结点存入作为顺序存储结构的一维数组，即将编号为i的结点存入一维数组的第i个单元。利用二叉树的性质⑤可求出结果

  • 第24题：

    单选题
    在平衡二叉树中插入一个结点后造成了不平衡，设最低的不平衡结点为A，并已知A的左孩子的平衡因子为0右孩子的平衡因子为1，则应作（）型调整以使其平衡。
    A

    LL

    B

    LR

    C

    RL

    D

    RR


    正确答案： D
    解析： 暂无解析

相关内容