在一元线性回归模型中,样本回归方程可表示为( )
题目
在一元线性回归模型中,样本回归方程可表示为( )
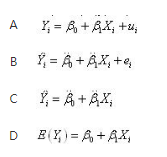
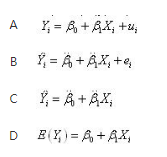
相似考题
参考答案和解析
答案:C
解析:
更多“在一元线性回归模型中,样本回归方程可表示为( ) ”相关问题
-
第1题:
下列回归模型中,属于一元线性回归模型的是( )。
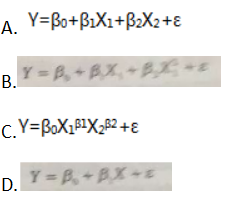 答案:D解析:回归模型可以用描述因变量Y如何依赖自变量X和误差项ε的方程来表示。只涉及一个自变量的一元线性回归模型可以表示为: Y = β0 + β1 X + ε
答案:D解析:回归模型可以用描述因变量Y如何依赖自变量X和误差项ε的方程来表示。只涉及一个自变量的一元线性回归模型可以表示为: Y = β0 + β1 X + ε
式中β0 和 β1为模型的参数
y 是 x 的线性函数(β0 + β1 X)加上误差项ε。 -
第2题:
关于一元线性回归的正确表述有( )。A.用来计算相关系数
B.是描述两个变量之间相关关系的最简单的回归模型
C.只涉及一个自变量
D.使用最小二乘法确定一元线性回归方程的系数
E.用决定系数来测度回归直线对样本数据的拟合程度答案:B,C,D,E解析:一元线性回归,是描述两个变量之间相关关系的最简单的回归模型。只及一个自变量,在现实中,模型的参数β0、β1都是未知的,需要利用样本数据去估计,采用的估计方法是最小二乘法。最小二乘法就是使得因变量的观测值与估计值之间的离差平方和最小来估计β0、β1的方法。决定系数,也称为R2,可以测度回归直线对样本数据的拟合程度。决定系数的取值在0到1之间,决定系数越接近1,回归直线的拟合效果越好。 -
第3题:
对于一元线性回归模型,样本回归函数的离差和等于0。( )答案:对解析:在一元线性回归模型中,残差的均值为0,则所有残差和为0,即样本回归函数的离差和为0。 -
第4题:
对一般的多元线性回归方程,其标准差表达为 式中的k为( )。
式中的k为( )。
Ⅰ.方程中的参数个数
Ⅱ.自变量数加上一个常数项
Ⅲ.一元线性回归方程中k=2
Ⅳ.二元线性回归方程中k=2
A、Ⅰ.Ⅱ.Ⅲ
B、Ⅰ.Ⅱ.Ⅳ
C、Ⅰ.Ⅲ.Ⅳ
D、Ⅱ.Ⅲ.Ⅳ答案:A解析:一般的多元线性回归方程,其标准差表达为: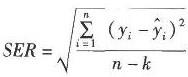
式中:k=方程中的参数个数(该数等于自变量数加上一个常数项)。注意,一元线性回归方程中k=2. D项二元线性回归方程中k=3 -
第5题:
若从样本获得的一元线性回归方程 是一条上升直线,则下列结论中,正确的是( )。
是一条上升直线,则下列结论中,正确的是( )。
A. a>0 B. aC. b>0 D. b答案:C解析: -
第6题:
多元线性回归模型与一元线性回归模型有哪些区别?
正确答案:多元线性回归模型与一元线性回归模型的区别表现在如下几个方面:一是解释变量的个数不同;二是模型的经典假设不同,多元线性回归模型比一元线性回归模型多了个“解释变量之间不存在线性相关关系”的假定;三是多元线性回归模型的参数估计式的表达更为复杂。 -
第7题:
回归分析模型可以是()
- A、一元线性回归模型
- B、多元线性回归模型
- C、系统聚类分析
- D、一元回归模型,多元回归模型
正确答案:D -
第8题:
在人力资源预测中,最常用的模型是()
- A、线性回归预测模型
- B、时间序列预测模型
- C、一元线性回归预测模型
- D、多元线性回归模型
正确答案:A -
第9题:
单选题一元线性回归模型的总体回归直线可表示为( )。AE(yi)=α+βxi
Byi=α+βxi
Cyi=α+βxi+ei
Dyi=α+βxi+mi
正确答案: A解析:
对一元线性回归方程yi=α+βxi+mi两边同时求期望,则有E(yi)=α+βxi。表明点(xi,E(yi))在E(yi)=α+βxi对应的直线上,这条直线即为总体回归直线(或理论回归直线)。 -
第10题:
单选题在人力资源预测中,最常用的模型是()A线性回归预测模型
B时间序列预测模型
C一元线性回归预测模型
D多元线性回归模型
正确答案: B解析: 暂无解析 -
第11题:
问答题如何利用一元线性回归分析的原理来求回归方程中两个回归系数a和b?正确答案: 两边取对数,化为线性问题。解析: 暂无解析 -
第12题:
单选题回归分析模型可以是()A一元线性回归模型
B多元线性回归模型
C系统聚类分析
D一元回归模型,多元回归模型
正确答案: D解析: 暂无解析 -
第13题:
回归模型Y=β0+β1X1+ β2X2+ε属于( )。A.一元回归模型
B.多元回归模型
C.线性回归模型
D.非线性回归模型
E.回归方程答案:B,C解析:根据自变量的多少,回归模型可以分为一元回归模型和多元回归模型。本题中,自变量有两个X1和X2,回归模型是多元回归模型。同时,回归模型描述的是两个变量X1、X2与Y的线性关系,回归模型是线性回归模型。 -
第14题:
设k为回归模型中的参数个数,n为样本容量。则对多元线性回归方程进行显著性检验时,所用的F统计量可表示为( )
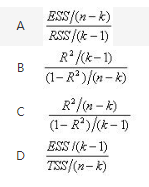 答案:B解析:
答案:B解析: -
第15题:
一元线性回归模型的总体回归直线可表示为( )。 答案:A解析:对一元回归方程
答案:A解析:对一元回归方程
两边同时取均值,则有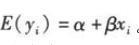
表明点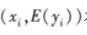
在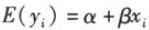
对应的直线上,这条直线即为总体回归直线(或理论回归直线)。
-
第16题:
某分析师建立了一元线性回归模型为 C i =β0 +β 1 Y i +u i ,根据已知样本,得到如下估计方程:
(回答71-72题)
在显著性水平α =0.05 的条件下,对于该一元回归模型的回归系数显著性分析正确的是( )。 答案:D解析:判断系数显著性的方法, 应参考 t 显著性水平/2 (样本数量-自由度) ,t 统计值大于 t 显著性水平/2(样本数量-自由度)才能视为通过显著性检验。
答案:D解析:判断系数显著性的方法, 应参考 t 显著性水平/2 (样本数量-自由度) ,t 统计值大于 t 显著性水平/2(样本数量-自由度)才能视为通过显著性检验。 -
第17题:
利用一元线性回归分析预测销售的第三步是()
- A、确定影响销售目标的因素
- B、收集整理因变量和自变量观察样本资料
- C、建立回归方程预测模型
- D、进行预测
正确答案:C -
第18题:
在一元线性回归方程中,回归系数表示自变量每变动一个单位时,因变量的平均变动值。()
正确答案:正确 -
第19题:
如何利用一元线性回归分析的原理来求回归方程中两个回归系数a和b?
正确答案: 两边取对数,化为线性问题。 -
第20题:
回归计算中,当()>()时,一元线性回归方程才具有真实意义。
正确答案:线性相关系数;0.999 -
第21题:
单选题一元线性回归模型的总体回归直线可表示为( )。AE(yi)=α+βxi
Byi=α+βxi
Cyi=α+βxi+ei
Dyi=α+βxi+μi
正确答案: B解析:
对一元回归方程Yi=α+βXi+μi两边同时取均值,则有E(yi)=α+βxi。这表明点(xi,E(yi))在E(yi)=α+βxi对应的直线上,这条直线叫做总体回归直线(或理论回归直线)。 -
第22题:
填空题回归计算中,当()>()时,一元线性回归方程才具有真实意义。正确答案: 线性相关系数,0.999解析: 暂无解析 -
第23题:
单选题一元线性回归模型的总体回归直线可表示为( )。[2016年5月真题]AE(yi)=α+βxi
Byi=α+βxi
Cyi=α+βxi+ei
Dyi=α+βxi+mi
正确答案: D解析:
对一元线性回归方程yi=α+βxi+mi两边同时求期望,则有E(yi)=α+βxi。表明点(xi,E(yi))在E(yi)=α+βxi对应的直线上,这条直线即为总体回归直线(或理论回归直线)。
