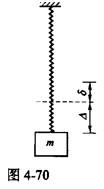
如图4-70所示,常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降Δ距离，则弹性力所做的功为（ ）。

题目
如图4-70所示,常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降Δ距离，则弹性力所做的功为（ ）。


相似考题

1.如图所示，实心物体A浸没在水中时，弹簧测力计示数为6N．将A制成空心体B（质量不变），放入装满水的溢水杯中，如图10乙所示，物体B处于悬浮状态，同时溢出水的质量为1kg．物体B空心部分的体积等于______m3．（g取10N/kg）

2.在弹性限度内，弹簧伸长的长度与所挂物体的质量成正比。一根弹簧不挂物体时长15厘米；所挂物体质量为3千克时，弹簧长16.8厘米，求弹簧总长y（厘米）与所挂物体质量x的（千克）之间的函数关系式。

3.质量为m的物体自高H处水平抛出，运动中受到与速度一次方成正比的空气阻力R作用，R=-kmv，k为常数。则其运动微分方程为：

4.设作用在一质量为2kg的物体上的力F在5S内均匀的从零到40N,开始时物体静止,则5S时物体的速度为()A、50m/sB、40m/sC、45m/sD、55m/s

更多“如图4-70所示,常数为k的弹簧下挂一质量为m的物体,若物体从静平衡位置(设静伸长为δ)下降Δ距离，则弹性力所做的功为（ ）。 ”相关问题

  • 第1题：

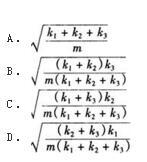
    如图所示，三根弹簧的刚性系数分别为k1，k2，k3，振体的质量为m，则此系统沿铅垂方向振动的固有圆频率为（　　）。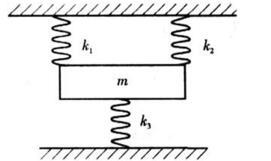


    答案：B
    解析：

  • 第2题：

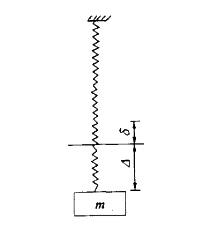
    图示一弹簧常数为k的弹簧下挂一质量为m的物体，若物体从静平衡位置（设静伸长为δ）下降Δ距离，则弹性力所做的功为：




    答案：D
    解析：
    提示：直接采用用弹性力做功的公式。

  • 第3题：

    如图所示，单摆由无重刚杆OA和质量为m的小球A构成，小球上连有两个刚度为k的水平弹簧，则摆微振动的固有频率为（　　）。


    答案：C
    解析：

  • 第4题：

    如图2-12所示，质量为4 kg的物体以5 m/s的速度冲上斜面．斜面的倾角为45°，物体与斜面间的摩擦因数μ=0.25．求：（取g=10m/s2）
    （1）物体能到达的最大高度；
    （2）物体克服摩擦力的功．


    答案：
    解析：
    本题是用牛顿方程解动力学问题的基本题． 以物体为研究对象．物体在斜面上，受到三个作用力：重力G，方向竖直向下；斜面支持力
    FN，方向垂直于斜面向上；滑动摩擦力Ff，方向平行于斜面向下．受力图如图2-17．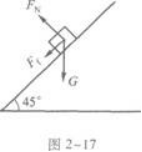

    （1）对物体用牛顿方程，取平行于斜面向下为正方向，有
    mgsin 45°+Ff=ma①
    取垂直于斜面向上为正方向，有
    FN－mgcos 45°=0②
    由式②得FN=mgcos 45°
    因此摩擦力为
    Ff=μFN=μmgcos 45°
    代入式①解得

    物体在斜面上做匀减速直线运动．由匀减速直线运动的速度一位移公式知，物体在斜面上运动的最大位移是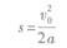

    把式③代入得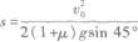

    由此得物体上升的最大高度为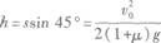

    代入题给数值得

    (2)物体在运动时克服重力和摩擦力做功．根据动能定理知
    Ek=WG+Wf


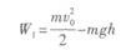
    代人已知数值得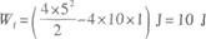

    【解题指要】本题是动力学和运动学结合的综合力学试题．本题考查的知识点是牛顿第二
    定律、摩擦力、匀减速直线运动和动能定理，解题的要点是先求出加速度a，它是联结动力学与运动学的桥梁．
    在求物体克服摩擦力的功时也可以由功的公式直接计算
    Wf=Ff·s=μmgcos 45°．s
    把s代入得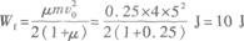

  • 第5题：

    如图所示结构，集中质量m在刚性梁的中点，EI=∞，弹簧刚度为k，该体系自振频率为（　　）。




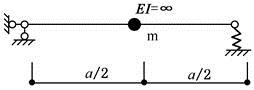
    答案：D
    解析：

  • 第6题：

    质量为2 k9的物体，在力F=2ti+4t2的作用下由静止从原点开始运动，求：
    (1)5 S末物体的速度和位置。
    (2)5 s内力所做的功。


    答案：
    解析：

  • 第7题：

    一个弹簧挂60N的重物时，弹簧伸长3cm，若该弹簧挂重为100N的物体时，其长度为15cm。求： （1）这个弹簧的劲度系数 （2）这个弹簧的原长L0


    正确答案: （1）2000N/m
    （2）10cm

  • 第8题：

    质量为5.0×103kg的物体，在高空受到的重力为4.8104N，该处的重力加速度g=（）m/s2。如果该处有另一质量为5kg的物体，放在竖直放置的劲度系数k=1000N/m的弹簧上，物体处于静止状态，则弹簧的压缩量x=（）m。


    正确答案:9.6；0.048

  • 第9题：

    设作用在质量为2Kg上的物体上的力F=6x（式中xF的单位为N，x的单位为m）。若物体由静止出发沿直线运动，则物体从0运动到x=2m过程中该力作的功W=12j，x=2m时物体的速率（）。


    正确答案:V=2√3m*s-1

  • 第10题：

    在轻质弹簧下端悬挂一质量为0.1kg的物体，当物体静止后，弹簧伸长了0.01m，取g=10m/s2。该弹簧的劲度系数为（）

    • A、1N/m
    • B、10N/m
    • C、100N/m
    • D、1000N/m

    正确答案:C

  • 第11题：

    质量为2kg的物体放在水平地板上，用一轻弹簧水平拉该物体，当物体刚开始运动时，弹簧伸长了3cm，当拉着物体匀速前进时，弹簧伸长2cm，已知弹簧的劲度系数为k="200"N/m（g="10"N/kg），求： （1）物体所受的最大静摩擦力为多少？ （2）物体和地板间的动摩擦因数。


    正确答案: （1）6N
    （2）0.2

  • 第12题：

    单选题
    一人将质量为5kg的物体从9m深的井底以2m/s的速度匀速提起，该过程中人对物体所做的功为（）
    A

    360J

    B

    450J

    C

    540J

    D

    720J


    正确答案： B
    解析： 暂无解析

  • 第13题：

    弹簧一物块直线振动系统位于铅垂面内，如图所示。弹簧刚度系数为k物块质量为m。若已知物块的运动微分方程为mx+kx=0，则描述运动的坐标Ox的坐标原点应为：


    答案：C
    解析：
    根据微分方程的推导过程。
    答案:C

  • 第14题：

    图示一刚性系数为k的弹簧下挂一质量为m的物块，当物块处于平衡时弹簧的静伸长为δ，则当物块从静平衡位置下降距离h时，弹性力所做的功W为：

    A. W = 1/2k[(h + δ)2-δ2] B. W = 1/2k[δ2-(h + δ)2] C. W = 1/2k(δ +h )2 D. 1/2kh2


    答案：B
    解析：
    提示:弹力作功W=1/2k( δ12-δ22)。

  • 第15题：

    一人站在10 m高的台上，把质量为0.4 kg的物体以5 m/s的速度抛出，物体落地时的速度为14 m/s.试求物体克服空气阻力所做的功.（g取10 m/s2）


    答案：
    解析：

  • 第16题：

    如图1—8所示，在水平力F的作用下，物重为G的某物体沿墙壁匀速下滑，若物体与墙壁之间的动摩擦因数为μ，则物体所受摩擦力的大小为（　　）



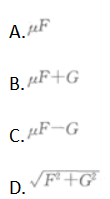    答案：A
    解析：

  • 第17题：

    如图．一不可伸长的光滑轻绳，其左端固定于0点，右端跨过位于O’点的固定光滑轴悬挂一质量为M的物体．00’，段水平，长度为L，绳子上套一可沿绳滑动的轻环。现在轻环上悬挂一钩码，平衡后物体上升L，则钩码的质量为( )。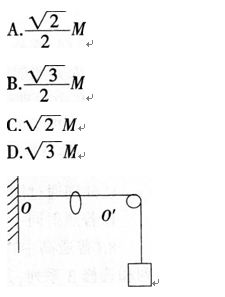


    答案：D
    解析：
    假设平衡后轻环的位置为P，平衡后，物体上升L，说明此时P00，恰好构成一个边长为L的正三角形，绳中张力处处相等，均为Mg，故钩码的重力恰好与P0，、P0拉力的合力等大反向，由三角函数关系可知．钩码的重力为 敝其质量为 ，故选D。

  • 第18题：

    质量为2k9的物体，在沿x方向的变力作用下，在x=0处由静止开始运动。设变力与x的关系如图所示。试由动能定理求物体在x=5，10，15m处的速率。



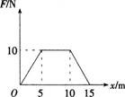    答案：
    解析：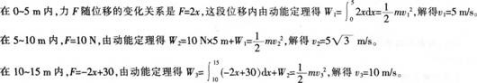

  • 第19题：

    一根弹簧挂0.5N的物体时长12cm，挂1N的物体时长14cm，则弹簧原长为（）cm，劲度系数k为（）N/m。


    正确答案:10；25

  • 第20题：

    一物体放到水平地板上，用一轻弹簧水平拉该物体，当物体刚开始运动时，弹簧伸长了3cm，当拉着物体匀速前进时，弹簧伸长了2cm，用弹簧测量此物体的重力时，弹簧伸长了10cm，己知弹簧的劲度系数为k=200N/m，（g=10N/kg）求： （1）物体所受的最大静摩擦力为多少？ （2）物体和地板间的动摩擦因数。


    正确答案: （1）6N
    （2）μ=0.2

  • 第21题：

    一劲度系数为k的轻弹簧下端固定在水平面上。今将一质量为m的物体轻轻放在弹簧上，立即放开手，则弹簧的最大压缩量为（）。


    正确答案:2mg/k

  • 第22题：

    半径为R具有光滑轴的定滑轮边缘绕一细绳，绳的下端挂一质量为m的物体绳的质量可以忽略，绳与定滑轮之间无相对滑动若物体下落的加速度为a，则定滑轮对轴的转动惯量J＝（）。


    正确答案:m（g-a）R2/a

  • 第23题：

    单选题
    设质量为100kg的物体从点M1（2，0，7）沿直线移动到点M2（0，3，1），则重力所做的功（长度单位为m，重力方向为Z轴负方向）为（）
    A

    0（J）

    B

    980（J）

    C

    5880（J）

    D

    2940（J）


    正确答案： D
    解析： 暂无解析

相关内容