已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。若解释变量所受教育水平的度量单位由年改为月，估计的截距项与斜率项有无变化？

题目

相似考题

1.设为回归模型中的解释变量的数目（不包括截距项），则要使含有截距项的模型能够得出参数估计量，所要求的最小样本容量为（）A.n≥k+1B.n≤k+1C.n≥30D.n≥3（k+1）

2.线性回归的基本假设不包括哪个()A.随机误差项是一个期望值为0的随机变量B.对于解释变量的所有观测值，随机误差项有相同的方差C.随机误差项彼此相关D.解释变量是确定性变量不是随机变量，与随机误差项之间相互独立E.随机误差项服从正态分布

4.已知含有截距项的三元线性回归模型估计的残差平方和为已知含有截距项的三元线性回归模型估计的残差平方和为，估计用样本容量为24，则随机误差项的方差估计量为（）。

参考答案和解析

再考虑解释变量度量单位变化的情形。设N*为用月份表示的新员工受教育的时间长度，则N*=12N，于是
E=α+βN+μ=α+β（N*/12）+μ
或E=α+（β/12）N*+μ
可见，估计的截距项不变，而斜率项将为原回归系数的1/12。
略

更多“已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。若解释变量所受教育水平的度量单位由年改为月，估计的截距项与斜率项有无变化？”相关问题

第1题：

回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（）
Ⅰ.被解释变量与解释变量之间具有线性关系
Ⅱ.随机误差项服从正态分布
Ⅲ.各个随机误差项的方差相同
Ⅳ.各个随机误差项之间不相关

A.Ⅰ.Ⅱ.Ⅲ.Ⅳ
B.Ⅰ.Ⅲ.Ⅳ
C.Ⅰ.Ⅱ.Ⅳ
D.Ⅱ.Ⅲ.Ⅳ

答案：A
解析：
—元线性回归模型为：yi=a+βi+mi（i=l,2,3,*,n）,其中yi为解解释变量Xi为解释变量;ui是一个随机变垦量.称为随机项。要求随机项u和自变量，Xi满足的统计假定如下：①每个ui均为独立同分右（IID、）,服从正态分右的随机变量，E（ui）=0,V（ui）=σ＾2常数②随机项ui与自变量的任一观察值Xi不相关，即COV（ui,i）=0
第2题：

DW检验的假设条件有（）。
Ⅰ.回归模型不含有滞后自变引作为解释变量
Ⅱ.随机扰动项满足
Ⅲ.回归模型含有不为零的截距项
Ⅳ.回归模型不含有滞后因变量作为解释变量

A、Ⅰ.Ⅱ.Ⅲ.Ⅳ
B、Ⅰ.Ⅱ.Ⅲ
C、Ⅱ.Ⅲ.Ⅳ
D、Ⅰ.Ⅱ.Ⅳ

答案：C
解析：
DW检验的假设条件为解释变量x为非随机变量，随机扰动项满足一阶自回归形式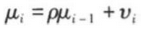

并且回归模型中不应含有滞后因变量作为解释变量，且回归模型含有不为零的截距项。
第3题：

DW检验的假设条件有（）。
Ⅰ.回归模型不含有滞后自变量作为解释变量
Ⅱ.随机扰动项，满足μi=ρμi-1+vi
Ⅲ.方回归模型含有不为零的截距项
Ⅳ.回归模型不含有滞后因变量作为解释变量

A.Ⅱ.Ⅲ.Ⅳ
B.Ⅰ.Ⅱ.Ⅳ
C.Ⅰ.Ⅱ.Ⅲ
D.Ⅰ.Ⅱ.Ⅳ

答案：A
解析：
DW检验假设条件为解释变量X为非随机变量，随机扰动项满足一阶自回归形式μi=ρμi-1+vi，并且回归模型中不应含有滞后因变量作为解释变量，且回归模型含有不为零的截距项。
第4题：

DW检验的假设条件有( )。

A.回归模型不含有滞后自变量作为解释变量
B.
C.回归模型含有不为零的截距项
D.回归模型不含有滞后因变量作为解释变量

答案：B,C,D
解析：
DW检验假设条件为解释变量X为非随机变量，随机扰动项满足一阶自回归元/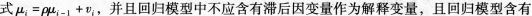

不为零的截距项。
第5题：

设为回归模型中的解释变量的数目（不包括截距项），则要使含有截距项的模型能够得出参数估计量，所要求的最小样本容量为（）
- A、n≥k+1
- B、n≤k+1
- C、n≥30
- D、n≥3（k+1）
正确答案:A
第6题：

应用DW检验需满足的条件不包括（）。
- A、模型包含截距项
- B、模型解释变量不能包含被解释变量的滞后项
- C、样本容量足够大
- D、解释变量为随机变量
正确答案:D
第7题：

按经典假设，线性回归模型中的解释变量应是非随机变量，且（）。
- A、与随机误差项不相关
- B、与残差项不相关
- C、与被解释变量不相关
- D、与回归值不相关
正确答案:A
第8题：

已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。从直观及经济角度解释α和β。

正确答案:α+βN为接受过N年教育的员工的总体平均起始薪金。当N为零时，平均薪金为α，因此α表示没有接受过教育员工的平均起始薪金。β是N每变化一个单位所引起的E的变化，即表示每多接受一年教育所对应的薪金增加值。
第9题：

对于固定影响的变截距面板数据模型，以下阐述正确的有（）。
- A、模型满足古典假定，可以采用OLS法对模型进行估计
- B、模型满足古典假定，可以采用最小二乘虚拟变量法（LSDV）对模型进行估计
- C、随机误差项不满足基本假设，可以采用广义最小二乘法（GLS）对模型进行估计
- D、随机误差项与解释变量相关，可以采用二阶段最小二乘方法（TSLS）对模型进行估计
- E、以上阐述都正确
正确答案:B,C,D
第10题：

线性回归模型的经典假设有（）。
- A、参数的线性性
- B、常参数
- C、扰动项均值为零，同方差性
- D、解释变量或自变量之间不相关
- E、扰动项序列无关
正确答案:A,B,C,D,E
第11题：

单选题
DW检验的假设条件有()。 I 回归模型不含有滞后自变量引作为解释变量 Ⅱ随机扰动项满足μi=ρμi-1+νi Ⅲ回归模型含有不为零的截距项 IV 回归模型不含有滞后因变量作为解释变量
A
I、II、III、IV
B
I、II、III
C
II、III、IV
D
I、II、IV

正确答案： C
解析： DW检验的假设条件为解释变量x为非随机变量，随机扰动项满足一阶自回归形式μi=ρμi-1+νi，并且回归模型中不应含有滞后因变量作为解释变量，且回归模型含有不为零的截距项。
第12题：

多选题
多元线性回归分析是建立在哪些假设基础上的？（　　）
A
解释变量之间不存在线性关系
B
自变量x₁，x₂，…，x_k是随机变量
C
所有随机误差项μ的均值为1
D
所有随机误差项μ服从正态分布N（0，σ²）

正确答案： C,A
解析：
多元线性回归模型满足如下基本假定：
①零均值假定，即E（μ_i）＝0（i＝1，2，…，n）；
②同方差与无自相关假定，即随机扰动项的方差和协方差满足：
Var（μ_i）＝σ²＝常数（i＝1，2，…，n）
Cov（μ_i，μ_j）＝0（i≠j）
③无多重共线性假定，即解释变量之间不存在线性关系；
④随机扰动项与解释变量互不相关，即：Cov（μ_i，x_ji）＝0（i＝1，2，…，n；j＝1，2，…，k）；
⑤正态性假定，随机扰动项μ_i服从正态分布，即μ_i～N（0，σ²）。
第13题：

回归分析是期货投资分析中重要的统计分析方法,而线性回归模型是回归分析的基础。线性回归模型的基本假设是（）
Ⅰ.被解释变量与解释变量之间具有线性关系
Ⅱ.随机误差项服从正态分布
Ⅲ.各个随机误差项的方差相同
Ⅳ.各个随机误差项之间不相关

A：Ⅰ.Ⅱ.Ⅲ.Ⅳ
B：Ⅰ.Ⅲ.Ⅳ
C：Ⅰ.Ⅱ.Ⅳ
D：Ⅱ.Ⅲ.Ⅳ

答案：A
解析：
—元线性回归模型为：yi=a+βi+mi（i=l,2,3,*,n）,其中yi为解解释变量Xi为解释变量;ui是一个随机变垦量.称为随机项。要求随机项u和自变量，Xi满足的统计假定如下：①每个ui均为独立同分右（IID、）,服从正态分右的随机变量，E（ui）=0,V（ui）=σ＾2常数②随机项ui与自变量的任一观察值Xi不相关，即COV（ui,i）=0
第14题：

DW检验的假设条件有（）。
Ⅰ.回归模型不含有滞后自变量作为解释变量
Ⅱ.随机扰动项，满足μi=ρμi-1+vi
Ⅲ.方回归模型含有不为零的截距项
Ⅳ.回归模型不含有滞后因变量作为解释变量

A：Ⅱ.Ⅲ.Ⅳ
B：Ⅰ.Ⅱ.Ⅳ
C：Ⅰ.Ⅱ.Ⅲ
D：Ⅰ.Ⅱ.Ⅳ

答案：A
解析：
DW检验假设条件为解释变量X为非随机变量，随机扰动项满足一阶自回归形式μi=ρμi-1+vi，并且回归模型中不应含有滞后因变量作为解释变量，且回归模型含有不为零的截距项。
第15题：

回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型的基本假设是（）。
I 被解释变量与解释变量之间具有线性关系
Ⅱ 随机误差项服从正态分布
Ⅲ 各个随机误差项的方差相同
Ⅳ 各个随机误差项之间不相关

A.I、Ⅱ、Ⅲ
B.I、Ⅲ、Ⅳ
C.Ⅱ、Ⅲ、Ⅳ
D.I、Ⅱ、Ⅲ、Ⅳ

答案：D
解析：
一元线性回归模型为：Yi=α+βxi+ui，(i=1，2，3，…，n)，其中Yi为被解释变量，xi为解释变量，ui是一个随机变量，称为随机项。要求随机项ui和自变量xi满足的统计假定如下：①每个ui均为独立同分布，服从正态分布的随机变量，且E(ui)=0， V(ui)=σ2=常数；②随机项ui与自变量的任一观察值xi不相关，即Cov(ui，xi)=0．
第16题：

回归分析是期货投资分析中重要的统计分析方法，而线性回归模型是回归分析的基础。线性回归模型中关于随机项μi的基本假设是（）。

A.随机项μi与自变量的任一观察值xi不相关
B.E（μi）=0，V（μi）=σu2=常数
C.每个随机项μi均为独立同分布，服从正态分布的随机变量
D.每个随机项μi之间均互不相关

答案：A,B,C,D
解析：
一元线性回归模型为：yi=α+βxi+μi，（i=1，2，3，…，n），其中，yi称为因变量或被解释变量；xi称为自变量或解释变量；μi是一个随机变量，称为随机（扰动）项；α和β是两个常数，称为回归参数；下标i表示变量的第i个观察值或随机项。随机项满足如下基本假定：
假定1，每个“μi=（i=1，2，3，…，n）”均为独立同分布，服从正态分布的随机变量，且E（μi）=0，y（μi）=σμ2=常数。
假定2，每个随机项，μi均互不相关，即：Cov（μi,μj）=O（i≠j）。
假定3，随机项μi与自变量的任一观察值xi不相关，即：Cov（μi，μj）=（i=1，2，3，…，n）
第17题：

已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。如果被解释变量新员工起始薪金的计量单位由元改为100元，估计的截距项、斜率项有无变化？

正确答案: 考察被解释变量度量单位变化的情形。以E*表示以百元为度量单位的薪金，则
E.E*×100=α+βN+μ
由此有如下新模型
E.=（α/100）+（β/100）N+（μ/100）
或E*=α*+β*N+μ*
这里α*=α/100，β*=β/100。所以新的回归系数将为原始模型回归系数的1/100。
第18题：

DW检验中要求有假定条件，在下列条件中不正确的是（）
- A、解释变量为非随机的
- B、随机误差项为一阶自回归形式
- C、线性回归模型中不应含有滞后内生变量为解释变量
- D、线性回归模型只能为一元回归形式
正确答案:D
第19题：

在线性模型中引入虚拟变量，可以反映（）。
- A、截距项变动
- B、斜率变动
- C、斜率与截距项同时变动
- D、分段回归
- E、以上都可以
正确答案:A,B,C,D,E
第20题：

已知回归模型E=α+βN+μ，式中E为某类公司一名新员工的起始薪金（元），N为所受教育水平（年）。随机扰动项的分布未知，其他所有假设都满足。对参数的假设检验还能进行吗？简单陈述理由。

正确答案:如果μ_t的分布未知，则所有的假设检验都是无效的。因为t检验与F检验是建立在μ的正态分布假设之上的。
第21题：

关于自回归模型，下列表述正确的有（）。
- A、估计自回归模型时的主要问题在于，滞后被解释变量的存在可能导致它与随机误差项相关，以及随机误差项出现自相关性
- B、Koyck模型和自适应预期模型都存在解释变量与随机误差项同期相关问题
- C、局部调整模型中解释变量与随机误差项没有同期相关，因此可以应用OLS估计
- D、Koyck模型与自适应预期模型不满足古典假定，如果用OLS直接进行估计，则估计量是有偏的、非一致估计
- E、无限期分布滞后模型可以通过一定的方法可以转换为一阶自回归模型
正确答案:A,B,C,D,E
第22题：

一般地，在一元线性回归分析过程中，回归分析是建立一系列假设基础上的，这些假设为（）
- A、回归模型因变量Y与自变量x之间具有线性关系。
- B、在重复抽样中，自变量x的取值是固定的，即假定x是非随机的。
- C、误差项ε的方差为零。
- D、误差项ε是独立随机变量且服从正态分布，即ε～N（0，σ2）。
正确答案:A,B,D
第23题：

单选题
DW检验的假设条件有（　　）。Ⅰ．回归模型不含有滞后自变量作为解释变量Ⅱ．随机扰动项满足mi＝rmi－1＋niⅢ．回归模型含有不为零的截距项Ⅳ．回归模型不含有滞后因变量作为解释变量
A
Ⅱ、Ⅳ
B
Ⅲ、Ⅳ
C
Ⅰ、Ⅱ、Ⅲ
D
Ⅱ、Ⅲ、Ⅳ

正确答案： A
解析：
DW检验假设条件为：解释变量X为非随机变量，随机扰动项满足一阶自回归形式m_i＝rm_i_－₁＋n_i，回归模型中不应含有滞后因变量作为解释变量，且回归模型含有不为零的截距项。

题目

相似考题

参考答案和解析

相关内容