在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．

题目
在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．

相似考题

1.△ABC中，AB=3，BC=4，则AC边的长满足（ ）。A．AC=5B．AC>1C．AC<7D．1<AC<7

2.在 △ABC中，∠C=90°，AB=10。（1）∠A=30°，求BC，AC（精确到0.01）；（2）∠A=45°，求BC，AC（精确到0.01）。

3.△ABC中，AB=13cm，BC=10cm，BC边上的中线AD=12cm.求AC

4.以下哪项是表达逻辑基本规律的公式A. A=AB. A≠┐AC. A∨BD. A∨┐A

更多“在△ABC中，AB=2，BC=3，B=60°，BD为AC边上的高．求AC，BD．”相关问题

  • 第1题：

    血清中的C1作用对象是（ ）

    A．C2aC3a

    B．C3aC5a

    C．C3bC4b

    D．C2C4

    E．C5aC3b


    正确答案：D

  • 第2题：

    试证明如下逻辑函数等式。(1) AB－＋AB－C=AB－;(2) AB(C＋C－)＋AC=AB＋AC;(3) A(BC＋BC)＋AC=A(BC)＋AC


    答案：(1)左边=AB-+AB-C=AB-(1+C)=AB-=右边(2)左边=AB(C+C-)+AC=AB+AC=右边(3)左边=A(BC+BC)+AC=A(BC)+AC=右边

  • 第3题：

    如图．已知圆⊙O是△ABC的外接圆，AD是圆⊙0的直径，且BD=BC，延长AD到E，且有∠EBD=∠CAB。

    (1)求证：BE是⊙0的切线；
    (2)若BC=√3，AC=5，求圆的直径AD及切线BE的长。


    答案：
    解析：
    (1)连接OB，∵AD是圆⊙O的直径'∴∠OBD+∠EBD=90°， ∵BD=BC,∴其劣弧所对的圆周角相等，即∠CAB=∠BAD，
    ∵AO=BO,∴∠BAD=∠ABO，
    又∠EBD=∠CAB,∴∠EBD=ABO,∴∠OBD+∠ABO=90°,∴∠OBE=90°，
    ∵B0是圆的半径，∴BE是⊙O的切线。
    (2)设圆的半径为r，连接CD交OB于F，

    设圆的半径为R，连接CD，.

  • 第4题：

    如图，Rt△ABC中，∠ABC=90o,AB=28 cm，以AB为直径的半圆与AC相交，图中的阴影部分①的面积比⑦的面积少28.28 cm2，求BC的长(π取3．14)。


    答案：
    解析：

  • 第5题：

    A.ⅠA
    B.ⅡA
    C.ⅡB
    D.ⅢA
    E.ⅣA

    镜下早期浸润癌

    答案：A
    解析：

  • 第6题：

    在△ABC中，已知AB＝5，AC＝3，∠A＝120°，则BC长为



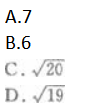    答案：A
    解析：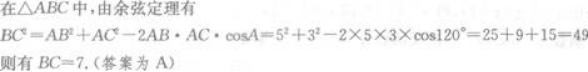

  • 第7题：

    在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．


    答案：
    解析：
    解：由余弦定理得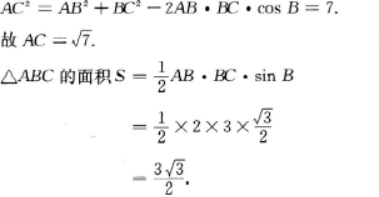

  • 第8题：

    在 ABC中，∠ABC=600，AB=4，BC=6，则AC=（）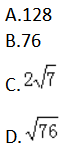


    答案：C
    解析：

  • 第9题：

    在三角形ABC，AB=4，AC=6，BC=8，D为BC的中点，则AD=




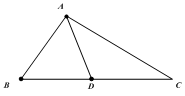
    答案：B
    解析：

  • 第10题：

    已知△ABC的三边长AC＝3，BC＝4，AB＝5，P为AB边上任意一点，则CP→ (BA→－BC→)的最大值为(　　)

    A、8
    B、9
    C、12
    D、15

    答案：B
    解析：

  • 第11题：

    逻辑函数Y=ABC+AC+BC的最简式为（）

    • A、Y=C
    • B、Y=BC+AB+BC
    • C、Y=ABC+AC+BC
    • D、Y=1

    正确答案:A

  • 第12题：

    Y=AB+BC+A=（）。

    • A、A+BC
    • B、A
    • C、BC
    • D、ABC

    正确答案:A

  • 第13题：

    对边相等,对角相等的凸四边形,是平行四边形吧?

    方法①∠B小于90°；

    左上为A，左下为B，右下为C，右上为D；

    已知∠B=∠D；AB=CD;

    证明：过A作AN⊥BC于N；

          过C作CM⊥AD于M；

          连接AC

    ∵AN⊥BC；CM⊥AD

    ∴∠ANB=∠DMC=90°

    又∵∠B=∠D；AB=CD

    ∴△ANB=△DMC(AAS）

    ∴AN=CM;BN=DM

    又∵∠ANB=∠DMC=90°，AC=AC

    ∴△ACD=△AMD（HL）

    ∴AM=DN

    又∵BN=DM

    ∴BD=AC

    ∵BD=AC；AB=CD

    ∴凸四边形ABCD为平行四边型。

    方法②∠B大于90°

    左上为A，左下为B，右下为C，右上为D；

    已知∠B=∠D；AB=CD;

    证明：延长CD,过A作AN⊥BC于N；

          延长AB,过C作CM⊥AD于M；

          连接AC

    ∵AN⊥BC；CM⊥AD

    ∴∠ANB=∠DMC=90°

    又∵∠B=∠D；AB=CD

    ∴△ANB=△DMC(AAS）

    ∴AN=CM;BN=DM

    又∵∠ANB=∠DMC=90°，AC=AC

    ∴△ACD=△AMD（HL）

    ∴AM=DN

    又∵BN=DM

    ∴BD=AC

    ∵BD=AC；AB=CD

    ∴凸四边形ABCD为平行四边型。

    方法③∠B等于90°

    证明：∵∠B=∠D=90°；AB=CD；AC=AC

    ∴△ABC=△ADC（HL）

    ∴AB=CB

    ∵BD=AC；AB=CD

    ∴凸四边形ABCD为平行四边型。

    有错吗？若我的证明有错请明示，我知道有个反例，但它是凹四边形。


    是平行四边形

  • 第14题：

    试用卡诺图化简如下逻辑函数式。(1) Y1=ABC＋ABC－＋B－(2) Y2=A＋AB－C＋AB(3) Y3=AC－＋AB－＋AB(4) Y4=AB－C－＋AC－＋C


    答案：(1) Y1=ABC+ABC-+B-(2) Y2=A+AB-C+AB(3) Y3=AC-+AB-+AB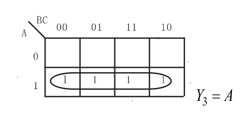(4) Y4=AB-C-+AC-+C

  • 第15题：

    锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F，


    答案：
    解析：

  • 第16题：

    A.ⅠA
    B.ⅡA
    C.ⅡB
    D.ⅢA
    E.ⅣA

    侵犯膀胱

    答案：E
    解析：

  • 第17题：

    A.ⅠA
    B.ⅡA
    C.ⅡB
    D.ⅢA
    E.ⅣA

    侵犯阴道下1/3宫旁浸润未达盆壁

    答案：D
    解析：

  • 第18题：

    A.ⅠA
    B.ⅡA
    C.ⅡB
    D.ⅢA
    E.ⅣA

    侵犯阴道上2/3，无宫旁浸润

    答案：B
    解析：

  • 第19题：

    在△ABC中，已知∠A=60°，且BC=4AB，求sinC(精确到0．001)。


    答案：
    解析：
    0．612

  • 第20题：

    已知△ABC和△A'B'C'满足AB:A'B'=AC:AC'=2:3,∠A+∠A'=,则△ABC和△A'B'C'的面积比为（ ）


    答案：E
    解析：
    特值法：假设AB=AC=2,A'B'=A'C'=3,∠A=∠A'=2，S:S'=12*2*2:12*3*3=4:9

  • 第21题：

    设A、B、C为随机事件，则( )。

    A.P(A-B-C)=P(A)-P(AB)-P(AC)-P(BC)+P(ABC)
    B.P(A-B-C)=P(A)-P(AB)-P(AC)+P(ABC)
    C.P(A-B-C)=P(A)-P(AB)-P(BC)+P(ABC)
    D.P(A-B-C)=P(A)-P(AC)-P(BC)+P(ABC)

    答案：B
    解析：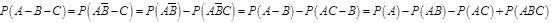

  • 第22题：

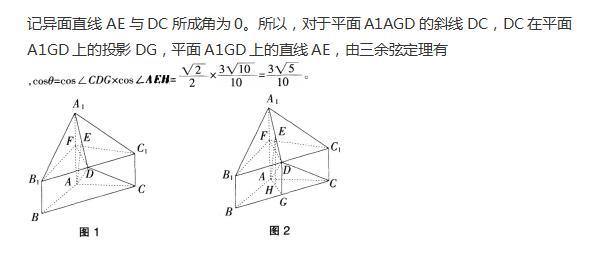
    (10分)如图，几何体A1B1C1-ABC中，AB=AC，AB⊥AC，棱AA1，BB1，CC1都垂直于面ABC，BC=AA1=2BB1=2CC1=4，D为B1C1的中点，E为A1D的中点。
    求证：(1)AE⊥BC；(3分)
    (2)求异面直线AE与DC所成角的余弦值。(7分)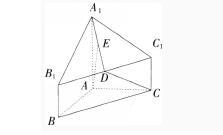


    答案：
    解析：

  • 第23题：

    有一镗削工件，三孔ABC的坐标尺寸如图，为检验上的需要，计算三孔ABC的中心距尺寸，正确的是（）。

    • A、AB=26.93，BC=23.35，AC=27.2
    • B、AB=26.93，BC=20.23，AC=26.5
    • C、AB=25.03，BC=23.35，AC=27.2
    • D、AB=25.03，BC=20.23，AC=27.2

    正确答案:A

相关内容