曲线y=x2+1与直线y=2x的交点坐标为()

题目

相似考题

1.关于直角坐标与极坐标,下列叙述正确的有()。A、两者都是正交坐标系;B、直角坐标中,x和y坐标线都是直线,有固定的方向,x和y的量纲均为L;C、极坐标中,ρ坐标线(φ=常数)和φ坐标线(ρ=常数)在不同点有不同的方向D、极坐标中，ρ坐标线为直线,φ坐标线为圆弧曲线;ρ的量纲为L,φ的量纲为1。

2.曲线y＝x2＋1在点(1，2)处的切线方程为__________．

3.作出函数y=3-2x的图象，根据图象回答下列问题：（1）y的值随着x值增大而__________;（2）图象与x轴的交点坐标是_________________，与y轴的交点坐标是_______________；（3）当x__________时，y＞0 。

4.曲线y=x3—2x在点（1，-1）处的切线方程为．

更多“曲线y=x2+1与直线y=2x的交点坐标为()”相关问题

第1题：

（2）抛物线y=ax²+bx+c与x轴的两交点的横坐标分别是-1/2,3/2,与y轴交点的纵坐标是-5。

解：设y=a(x-x1)(x-x2) =a(x+1/2)(x-3/2) 与y轴的交点的纵坐标是-5 所以y=20(x+1/2)(x-3/2)/3 化简得y=20x2/3-20x/3-5
第2题：

：直线y=kx+b(k≠0)与坐标轴交点的个数为（）。
A．1
B．2
C．0
D．1或2

正确答案：D

因为y=kx+6，当b----0时为正比例函数只与坐标轴相交于原点即只有一个交点，当be=0时为一次函数应与x轴、Y轴分别有一个交点即此时有两个交点，因此答案为D。
第3题：

如图所示，已知A，B为直线L：y=mx-m+2与抛物线y=x2的两个交点。
(1)直线ι经过一个定点C，试求出点C的坐标；(2分)
(2)若m=-1，已知在直线L下方的抛物线上存在一点P(点P与坐标原点0不重合)，且△ABP的面积为（3√13）/2，求点P的坐标。(6分)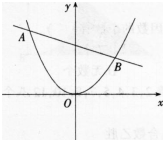

答案：
解析：
(1)直线L：y=m(x-1)+2，当x=1时，y的取值与m无关，此时y=2，所以直线过定点(1，2)；
第4题：

设圆C与圆（x-5）2+y2=2关于直线y=2x对称，则圆C的方程为

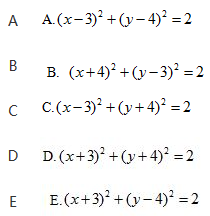答案：E
解析：
第5题：

在空间直角坐标系中，抛物柱面y2=2x与平面x-y-2=0的交为（）

A.椭圆
B.两条平行直线
C.抛物线
D.双曲线

答案：B
解析：
抛物柱面y2=2x与平面x-y-2=0可看作是xOy平面内的曲线y2=2x与直线x-y-2=0沿平行。轴方向平移得到的面。联立方程y2=2x与方程x-y-2=0，消去y得x2-6x+4=0，其中△=62-4×4×1=20＞0，故在zOy片面内曲线y2=2x与直线x-y-2=0的交是两个点。沿着平行于2轴的方向平移这两个点，就得到了两条平行直线，即抛物柱面y2=2x与平面x-y-2=0的交为平行于z轴的两条平行直线.
第6题：

粘度法实验中，当用外推法做图求[η]值时，如η_sp/C、lnη_r/C与y轴三条直线不能相交于一点时，应该用哪两条直线交点作为[η]值较为准确（）。
- A、η_sp/C与lnη_r/C的交点
- B、η_sp/C与y轴的交点
- C、lnη_r/C与y轴的交点
正确答案:B
第7题：

已知直线的斜率为0.5，起点为（X10.，Y10.），终点的X坐标为X50.，则终点的Y坐标为（）。
- A、Y25.
- B、Y27.5
- C、Y28.
- D、Y30.
正确答案:D
第8题：

测量使用的平面直角坐标是以两条互相垂直线的交点为坐标原点，南北方向的纵轴为x轴，以东西方向的横轴为y轴。

正确答案:正确
第9题：

填空题
曲线y＝y（x）经过原点且在原点处的切线与直线2x＋y＝6平行，而y＝y（x）满足方程y″－2y′＋5y＝0，则此曲线的方程为____。

正确答案： y=-e^xsin2x
解析：
所求曲线方程满足方程y″－2y′＋5y＝0，其特征方程为r²－2r＋5＝0，解得r₁_，₂＝1±2i。故方程y″－2y′＋5y＝0的通解为y＝e^x（c₁cos2x＋c₂sin2x）。又因为所求曲线经过原点，且在原点处的切线与直线2x＋y＝6平行，故y（0）＝0，y′（0）＝－2，将其代入y＝e^x（c₁cos2x＋c₂sin2x）得c₁＝0，c₂＝－1。故所求曲线方程为y＝－e^xsin2x。
第10题：

问答题
计算抛物线y2=2x与直线y=x-4所围成平面图形

正确答案：
解析：
第11题：

单选题
一直线的起点坐标在坐标原点，终点坐标为A（xa、ya），刀具的坐标为P（x、y）。用逐点比较法对该直线进行插补时的偏差函数是（）。
A
F＝x·y－x_a·y_a；
B
F＝x_a·y－y_a·x；
C
F＝x_a·x－y_a·y；
D
F＝x_a+y_a－x－y

正确答案： B
解析：暂无解析
第12题：

单选题
用简单迭代法求方程f（x）=0的实根，把方程f（x）=0表示成x=φ（x），则f（x）=0的根是（）。
A
y=φ（x）与x轴交点的横坐标
B
y=x与y=φ（x）交点的横坐标
C
y=x与x轴的交点的横坐标
D
y=x与y=φ（x）的交点

正确答案： C
解析：暂无解析
第13题：

若方程Y=a＋bX中的截距a<0，说明A、随着X的增大，Y增大B、随着X的增大，Y减少C、随着X的减少，Y减少D、回

若方程Y=a+bX中的截距a<0，说明
A、随着X的增大，Y增大
B、随着X的增大，Y减少
C、随着X的减少，Y减少
D、回归直线与Y轴的交点在原点下方
E、回归直线与Y轴的交点在原点上方

参考答案：B
第14题：

设曲线y=^e1?x2与直线x=-1的交点为P，则曲线在点P处的切线方程是（　　）

A．2x-y+2=0
B．2x+y+1=0
C．2x+y-3=0
D．2x-y+3=0

答案：D
解析：

@##
第15题：

已知直线在x轴上的截距为-1，在y轴上的截距为1，又抛物线y=x2+bx+c的顶点坐标为(2，-8)，求直线和抛物线两个交点横坐标的平方和．

答案：
解析：

设直线与抛物线两交点的横坐标为x1和x2，则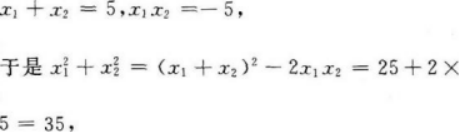

即直线与抛物线两交点的横坐标的平方和为35．
第16题：

若方程Y=a+bX中的截距a＜0，说明

A.随着X的增大，y减少
B.随着X的减少，y减少
C.随着X的增大，y增大
D.回归直线与y轴的交点在原点上方
E.回归直线与y轴的交点在原点下方

答案：E
解析：
第17题：

（）曲线的上端与横坐标的交点与（）曲线下端与横坐标的交点在同一垂直线上。

正确答案:θ（沉物）；β（浮物）
第18题：

用简单迭代法求方程f（x）=0的实根，把方程f（x）=0表示成x=φ（x），则f（x）=0的根是（）。
- A、y=φ（x）与x轴交点的横坐标
- B、y=x与y=φ（x）交点的横坐标
- C、y=x与x轴的交点的横坐标
- D、y=x与y=φ（x）的交点
正确答案:B
第19题：

若方程Y=a+bX中的截距a<0，说明（）
- A、随着X的增大，y增大
- B、随着X的增大，y减少
- C、随着X的减少，y减少
- D、回归直线与y轴的交点在原点下方
- E、回归直线与y轴的交点在原点上方
正确答案:D
第20题：

由曲线y=3-x2与直线y=2x所围成的图形的面积是（）．
- A、11/3
- B、22/3
- C、32/3
- D、86/3
正确答案:C
第21题：

单选题
直线ax—by＋ab＝o（其中ab≠0）与y轴的交点坐标是（　　）．
A
（0，－b）
B
（0，b）
C
（0，－a）
D
（0，a）

正确答案： D
解析：
由题意得，设交点坐标为（0，y₁），则－by₁＋ab＝0，∵ab≠0，∴b≠0．∴y₁＝a，交点坐标为（0，a）．
第22题：

单选题
一曲线在其上任一点的切线的斜率为－2x/y，则此曲线是（　　）。
A
直线
B
抛物线
C
椭圆
D
圆

正确答案： D
解析：
由题意可知，y′＝－2x/y，解此一阶微分方程得y²/2＝－x²＋c，即曲线为椭圆。
第23题：

单选题
由曲线y=3-x2与直线y=2x所围成的图形的面积是（）．
A
11/3
B
22/3
C
32/3
D
86/3

正确答案： A
解析：暂无解析

曲线y=x2+1与直线y=2x的交点坐标为()

题目

相似考题

更多“曲线y=x2+1与直线y=2x的交点坐标为()”相关问题

相关内容