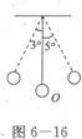
甲、乙两个单摆，摆线长度相等，甲球质量是乙球的2倍，现在把两球分别向两边拉开3°和5°（如图6--16），然后同时释放，则两球相遇在 （　　） A.O点左侧 B.O点右侧 C.O点 D.无法确定

题目
甲、乙两个单摆，摆线长度相等，甲球质量是乙球的2倍，现在把两球分别向两边拉开3°和5°（如图6--16），然后同时释放，则两球相遇在 （　　）

A.O点左侧
B.O点右侧
C.O点
D.无法确定
相似考题

1.甲.乙和丙.丁比赛，甲发球给乙，丙在球着地前触网，然后由于球落在发球区外，判甲发球失误。此题为判断题(对，错)。

2.有四个外表看起来没有分别的小球，它们的重量可能有所不同。取一个天平，将甲、乙归为一组，丙、丁归为另一组，分别放在天平两边，天平是基本平衡的。将乙、丁对调一下，甲、丁一边明显要比乙、丙一边重得多。可奇怪的是，我们在天平一边放上甲、丙，而另一边则放上乙，还没有来得及放上丁时，天平就压向了乙一边。请你判断，甲球与丁球哪个更重?（ ）A．丁球比甲球重B．丁球比甲球轻C．甲球与丁球同样重D．无法确定甲球与丁球的轻重

3.甲/乙对丙/丁的双打比赛，决胜局3：3换边后，应由甲再发一分球，可是乙发了该分球进行比赛，期间主裁发觉有误，则下次轮回甲/乙组发球时该由谁来发球( )A.甲B.乙C.甲、乙各发一球

4.甲乙两人共有100个玻璃球，若把甲的玻璃球的四分之一给乙，乙将比甲多九分之七，则甲原来有多少个玻璃球?( )A．40 B．48 C．56 D．60

更多“甲、乙两个单摆，摆线长度相等，甲球质量是乙球的2倍，现在把两球分别向两边拉开3°和5°（如图6--16），然后同时释放，则两球相遇在 （　　） ”相关问题

  • 第1题：

    甲、乙、丙各有球若干个，甲给乙的球如乙现有的那么多球，甲也给丙如丙现有的那么多球，然后乙也按甲和丙手中球数分别给甲、丙添球，最后丙也按甲和乙手中的球数分别给 甲、乙添球，此时三人都各有16个球，问开始时甲有多少个?（ ） A．26 B．14 C．8 D．10


    正确答案：A
    本题属于复杂的还原问题，要求开始时甲的数量，需要从第三次添球开始向前推。第三次添球后，甲、乙、丙三人手中都是16个球，第三次添球之前甲的球数是16÷2=8个；同样，乙的球数是16÷2=8个；第三次添球前丙的球数是16+8+8=32个；第二次添球之后，甲、乙、丙的球数分别是8，8，32。与上面相似，可以求得第二次添球之前甲的球数是8--2=4个；丙的球数是32"2=16个；乙的球数是8+16+4=28个；第一次添球之后，甲、乙、丙的球数分别为4，28，16。第一次添球前乙的球数是28÷2=14个；丙的球数是16-2=8个；甲的球数是4+14+8=26个；所以，开始时，甲、乙、丙三人手中的球数分别为26、14、8。(注意：倒推是解还原问题的主要方法。对于较复杂的还原问题，还常常根据题目特点，将倒推与其他方法结合起来求解。)故选A。

  • 第2题：

    甲袋有白球3只，红球7只，黑球l5只。乙袋有白球10只，红球6只，黑球9只。现从两袋中各取一个，试求两球颜色相同的概率约为（ ）。

    A．0.17

    B．0.33

    C．0.45

    D．0.8


    正确答案：B

  • 第3题：

    甲、乙、丙各有球若干，甲给乙的球和乙现有的球一样多，甲给丙的球和丙现有的球一样多，然后乙也按甲和丙手中的球数分别给甲、丙添球，最后丙也按甲、乙手中的球数分别给甲、乙添球，此时三人都各有球16个，开始时甲有多少个球？（ ）

    A．26

    B．24

    C．32

    D．30


    正确答案：A
    从最后一次开始向前推，第三次，甲有8个，乙有8个，丙有32个，第二次，甲有4个，乙有28个，丙有16个，第一次，甲有26个，乙有14个，丙有8个。

  • 第4题：

    盒中有8个球，上面分别写着2，3，4，5，7，8，10，12八个数，甲乙两人玩摸球游戏，下面规则中对双方都公平的是()。

    A.任意摸一球，是质数甲胜，是合数乙胜
    B.任意摸一球，是2的倍数甲胜，是3的倍数乙胜
    C.任意摸一球，小于5甲胜，大于5乙胜’
    D.任意摸一球，是奇数甲胜，是偶数乙胜

    答案：A
    解析：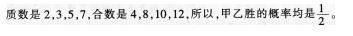

  • 第5题：

    现有3个箱子，依次放人1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放人其箱内球数的2、3、4倍。两次共放了22个球，最终甲箱中的球比乙箱（）

    A.多1个
    B.少1个
    C.多2个
    D.少2个

    答案：A
    解析：
    三个箱子臞来一共6个球，所以新放进16个，即2甲+3乙+4丙=16,根据奇数偶数的性质，乙是偶数，所以乙是2个球的箱子,所以甲=3,丙=1，因此甲放了9个球，乙放了8个球，多1个。

  • 第6题：

    甲袋内有2个白球3个黑球，乙袋内有3个白球1个黑球，现从两个袋内各摸出1个球，摸出的两个球都是白球的概率是( )



    答案：C
    解析：
    【考情点拨】本题主要考查的知识点为相互独立事件同时发生的概率． 【应试指导】由已知条件可知此题属于相互独立同时发生的事件，从甲袋内摸到白球的概率

  • 第7题：

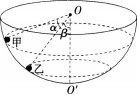
    如图所示，有一个固定且内壁光滑的半球面，球心为0，最低点为O′，在其内壁上有两个质量相同、可视为质点的小球甲和乙，分别在高度不同的水平面内做匀速圆周运动，若甲乙两球与O点的连线与竖直线O0′的夹角分别为α=53°和β=37°，则 (已知sin37°=3/5，cos37°=4/5，sin53°=4/5，cos53°=3/5)


    A．甲、乙两球运动周期之比为3／4

    B．甲、乙两球运动周期之比为√3/4

    C．甲、乙两球所受支持力之比为3／4

    D．甲、乙两球所受支持力之比为√3/4

    答案：B
    解析：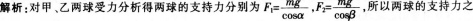

  • 第8题：

    现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。

    • A、多1个
    • B、少1个
    • C、多2个
    • D、少2个

    正确答案:A

  • 第9题：

    下列哪种情况不应判球回后场违例（）

    • A、骑跨中线站立原地拍运球
    • B、两人骑跨中线站立互相传球
    • C、甲5在前场传球球滚至后场甲5与乙5争抢此球甲5先触及球
    • D、甲5在本方前场防守将对方的球打至本方后场甲7接住

    正确答案:D

  • 第10题：

    有甲、乙两个玻璃球，甲球半径的3倍等于乙球半径的2倍，甲球重40克，则乙球重( )克。

    • A、140
    • B、135
    • C、130
    • D、125

    正确答案:B

  • 第11题：

    单选题
    甲8跳起投篮，乙8跳起用单手封盖，然后两人持球落地，此球应判（）
    A

    甲8走步违例

    B

    乙8防守犯规

    C

    双方争球

    D

    甲8两次运球


    正确答案： C
    解析： 暂无解析

  • 第12题：

    填空题
    甲袋中有5只白球，5只红球，15只黑球，乙袋中有10只白球，5只红球，10只黑球，从两袋中各取一球，则两球颜色相同的概率为____。

    正确答案： 9/25
    解析：
    分别记白、红、黑为第1、2、3种颜色，设Ai：“从甲袋中取出的是第i种颜色的球”；Bi：“从乙袋中取出的是第i种颜色的球”；C：“取出的球的颜色相同”。则C＝A1B1∪A2B2∪A3B3。
    故P（C）＝P（A1B1∪A2B2∪A3B3）＝P（A1B1）＋P（A2B2）＋P（A3B3）＝P（A1）P（B1）＋P（A2）P（B2）＋P（A3）P（B3）＝（5/25）×（10/25）＋（5/25）×（5/25）＋（15/25）×（10/25）＝9/25。

  • 第13题：

    甲、乙、丙各有球若干个，甲给乙的球等于乙现有的那么多球，甲给丙的球等于丙现有的那么多球，然后乙也按甲和丙手中球数分别给甲、丙添球，最后丙也按甲和乙手中的球数分别给甲、乙添球，此时三人各有16个球，问刚开始时甲有多少个球?（　　）

    A.26　　　　B.14　　　　C.8　　　　D.10


    本题正确答案为A。本题可以使用倒推法求取答案。
    　　由题意知，第三次添球后甲、乙、丙三人手中各有16个球。故在第三次添球前，甲、乙的球为16÷2＝8，而丙的球是16+8+8＝32（个）球。
    　　在第二次添球前，甲的球为8÷2＝4（个），丙为32÷2＝16（个），乙的球数为8+4+16＝28（个）。
    　　第一次添球前，乙的球为28÷2＝14（个），丙的球为16÷2＝8（个），甲的球为4+14+8＝26（个），故A项正确。

  • 第14题：

    甲乙两人共有100个玻璃球，若把甲的玻璃球的四分之一给乙，乙将比甲多九分之七，则甲原来有多少个玻璃球?

    A．40

    B．48

    C．56

    D．60


    正确答案：B
    [答案] B。解析：可用代入法解决。

  • 第15题：

    在同一地点的甲、乙两个单摆，摆球的质量之比为1：4，摆长之比为4：1，那么，在甲振动10次的 时间内，乙振动__________次．


    答案：
    解析：
    20

  • 第16题：

    如图所示，甲、乙两个大小相同的实心金属球放置在光滑水平面上，甲球以水平向右的速度碰撞静止的乙球。已知甲球质量大于乙球，则有关碰撞后的情形。下列说法正确的是（ ）。

    A.甲球可能静止
    B.乙球可能静止
    C.甲球可能向左运动
    D.甲球一定向右运动

    答案：D
    解析：

  • 第17题：

    有甲、乙两个口袋,两袋中都有3个白球2个黑球,现从甲袋中任取一球放入乙袋,再从乙袋中任取4个球,设4个球中的黑球数用X表示,求X的分布律.


    答案：
    解析：

  • 第18题：

    如图3所示，A、B两小球从相同高度同时水平抛出，经过时间t在空中相遇，若两球的抛出速度都变为原来的2倍，则两球从抛出到相遇经过的时间为( )。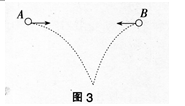



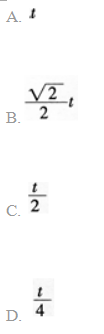    答案：C
    解析：

  • 第19题：

    将单摆摆球拉到悬点后由静止放开，到摆线伸直的时间为t1，将摆球拉开使摆线与竖直方向的夹角为3°，从静止放开摆球回到平衡位置的时间为t2，则t1∶t2=（）。


    正确答案:3√2：π

  • 第20题：

    从某一高度先后由静止释放两个相同的小球甲和乙，若两球被释放的时间间隔为1s，在不计空气阻力的情况下，它们在空中的运动过程中，说法正确的是（）

    • A、甲、乙两球的距离越来越大，甲、乙两球的速度之差越来越大
    • B、甲、乙两球的距离始终保持不变，甲、乙两球的速度之差保持不变
    • C、甲、乙两球的距离越来越大，甲、乙两球的速度之差保持不变
    • D、甲、乙两球的距离越来越小，甲、乙两球的速度之差越来越小

    正确答案:C

  • 第21题：

    甲8跳起投篮，乙8跳起用单手封盖，然后两人持球落地，此球应判（）

    • A、甲8走步违例
    • B、乙8防守犯规
    • C、双方争球
    • D、甲8两次运球

    正确答案:A

  • 第22题：

    为丰富员工业余文化生活，某单位组织了乒乓球、象棋、羽毛球三项比赛。每两个人之间都要通过比试这3项分出胜负，假设没有平局，同时比赛的2个人甲和乙，甲在乒乓球战胜乙的概率是50%、甲在象棋战胜乙的概率是50%、甲在羽毛球战胜乙的概率是40%，那么比试下来，甲战胜乙的概率是（）

    • A、0.3
    • B、0.35
    • C、0.4
    • D、0.45

    正确答案:D

  • 第23题：

    单选题
    现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。
    A

    多1个

    B

    少1个

    C

    多2个

    D

    少2个


    正确答案： A
    解析： 由题知，甲、乙、丙3个箱子里最终的球数为原球数的3、4、5倍，而原来的球数是1或2或3，设三个箱子原来分别有x、y、z个球，则有x+y+x=6……（1），3x+4y+5x=22……（2），因为比较的是甲和乙的关系，因此我们将z消去，用5×（1）-（2）得2x+y=8.如果x=1，y=6，不符合，如果x=2，y=4，不符合，于是x=3，y=2，选A。

相关内容