11 、点 A （ 2 ， y 1 ）、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ）．

题目

11 、点 A （ 2 ， y 1 ）、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关

系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ）．

相似考题

1.已知“a=dict(x=1,y=dict(y1=2,y2=3))”且“b=a.copy()”,则执行“a['y']['y1']=10”后,则print(b)的输出结果为()。A、{x=1,y={y1=10,y2=3}}B、{x=1,y={y1=2,y2=3}}C、{'x':1,'y':{'y1':10,'y2':3}}D、{'x':1,'y':{'y1':2,'y2':3}}

2.在同一直角坐标系内一次作出函数y=x+1，y=2x+1，y=3x+1的图象。（1）这几个图象之间有什么差别，又有什么联系？（2）一次函数y=kx+b的一次项系数k对函数的图象有什么影响？

3.如果曲线y=f(x)在点（x,y）处的切线斜率与x2成正比，并且此曲线过点（1，-3）和（2，11），则此曲线方程为（）。A. y=x3-2B. y=2x3-5C. y=x2-2D. y=2x2-5

4.作出函数y=3-2x的图象，根据图象回答下列问题：（1）y的值随着x值增大而__________;（2）图象与x轴的交点坐标是_________________，与y轴的交点坐标是_______________；（3）当x__________时，y＞0 。

参考答案和解析

正确答案：

考点：二次函数图象上点的坐标特征。

分析：本题需先根据已知条件求出二次函数的图象的对称轴，再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系．

解答：解：∵二次函数y=x²﹣2x+1的图象的对称轴是x=1，

在对称轴的右面y随x的增大而增大，

∵点A（2，y1）、B（3，y2）是二次函数y=x²﹣2x+1的图象上两点，

23，

∴y1y2．

故答案为：．

点评：本题主要考查了二次函数图象上点的坐标特征，在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键．

更多“11 、点 A ( 2 , y 1 ) 、 B ( 3 , y 2 )是二次函数 y=x 2－ 2x＋1 的图象上两点,则 y 1 与 y 2 的大 ”相关问题

第1题：

设线性无关的函数y1、y2、y3都是二阶非齐次线性方程y″+p(x)y′+q(x)y=f(x)的解，C1、C2是任意常数，则该非齐次方程的通解是( )。

A.C1y1+C2y2+y3
B.C1y1+C2y2-(C1+C2)y3
C.C1y1+C2y2-(1-C1-C2)y3
D.C1y1+C2y2+(1-C1-C2)y3

答案：D
解析：
根据解的性质知，y1-y3，y2-y3均为齐次方程的解且线性无关，因此C1(y1-y3)+C2(y2-y3)为齐次方程的通解，从而C1(y1-y3)+C2(y2-y3)+y3=C1y1+C2y2+(1-C1-C2)y3为非齐次方程的通解。
第2题：

设线性无关函数y1、y2、y3都是二阶非齐次线性方程y''+p(x)y‘+Q(x)y =f(x)的解，c1、c2是待定常数。则此方程的通解是：
A. c1y1+c2y2+y3 B. c1y1+c2y2-(c1+c3)y3
C. c1y1+c2y2-(1-c1-c2)y3 D. c1y1+c2y2+(1-c1-c2)y3

答案：D
解析：
提示：y1-y3、y2-y3为对应齐次方程的特解，为非齐次方程的特解。
第3题：

如果曲线Y=f(x）在点（x，y)处的切线斜率与x2成正比，并且此曲线过点(1，-3)和(2，11)，则此曲线方程为（　　）．

A.Y=3-2
B.Y=2x3-5
C.Y=x2-2
D.Y=2x2-5

答案：B
解析：
由曲线过点(1，-3)排除A、C项.由此曲线过点(2，11)排除D，故选B.Y=2x3-5显然过点(1，-3)和(2，11)，且它在(x，Y)处的切线斜率为6x2，显然满足与x2成正比.
第4题：

若y2(x)是线性非齐次方程y'+p(x)y=q(x)的解，y1(x)是对应的齐次方程y'+p(x)y=0的解，则下列函数也是y'+p(x)y=q(x) 的解的是（）。
A.y=Cy1(x)+y2(x) B. y=y1(x)+Cy2(x)
C.y=C[y1(x)+y2(x)] D.y=Cy1(x)-y2(x)

答案：A
解析：
提示：齐次方程的通解加上非齐次的特解仍是非齐次的解。
第5题：

设线性无关函数y₁、y₂、y₃都是二阶非齐次线性方程y″+P（x）y′+Q（x）y=f（x）的解，C₁、C₂是待定常数。则此方程的通解是：（）
- A、C₁y₁+C₂y₂+y₃
- B、C₁y₁+C₂y₂-（C₁+C₃）y₃
- C、C₁y₁+C₂y₂-（1-C₁-C₂）y₃
- D、C₁y₁+C₂y₂+（1-C₁-C₂）y₃
正确答案:D
第6题：

设随机变量X服从[0，2]上的均匀分布，Y=2X+1，则D（Y）=（）。

正确答案:4/3
第7题：

设X在[0，1]上服从均匀分布，Y=2X+1，则下列结论正确的是（）
- A、Y在[0，1]上服从均匀分布
- B、Y在[1，3]上服从均匀分布
- C、Y在[0，3]上服从均匀分布
- D、P{0≤Y≤1}=1
正确答案:B
第8题：

单选题
线性无关的函数y1（x），y2（x），y3（x）都是二阶非齐线性方程y"+a1（x）y’+a2（x）y=f（x）的解。C1，C2是任意常数，则该方程的通解是（）。
A
y=C₁y₁+C₂y₂+y₃
B
y=C₁y₁+C₂y₂+（C₁+C₂）y₃
C
y=C₁y₁+C₂y₂-（1-C₁-C₂）y₃
D
y=C₁y₁+C₂y₂+（1-C₁-C₂）y₃

正确答案： B
解析：选项（D）变形为y=C₁（y₁-y₃）+C₂（y₂-y₃）+y₃，y₁-y₃，y₂-y₃是对应齐次方程的解，且它们线性无关，y₃是非齐方程的一个特解，由线性方程解的结构可见（D）是通解。
第9题：

单选题
设随机变量X～N（0，1），Y～N（1，4），且相关系数ρXY＝1，则（　　）。
A
P{Y＝－2X－1}＝1
B
P{Y＝2X－1}＝1
C
P{Y＝－2X＋1}＝1
D
P{Y＝2X＋1}＝1

正确答案： A
解析：
令Y＝aX＋b，因为X～N（0，1），Y～N（1，4），则E（Y）＝aE（X）＋b＝1，得b＝1，D（Y）＝a²D（X）＝4，则a＝±2。
又ρ_XY＝1，则a＞0，故a＝2。故应选D。
第10题：

单选题
设函数y1（x）、y2（x）、y3（x）线性无关，且都是二阶非齐次线性方程y″＋p（x）y′＋q（x）y＝f（x）的解，又c1与c2为任意常数，则该非齐次线性方程的通解可表示为（　　）。
A
c₁y₁＋c₂y₂＋y₃
B
c₁y₁＋c₂y₂－（c₂＋c₁）y₃
C
c₁y₁＋c₂y₂－（1－c₁－c₂）y₃
D
c₁y₁＋c₂y₂＋（1－c₁－c₂）y₃

正确答案： C
解析：
由解的结构可知，y₁－y₃和y₂－y₃是对应齐次方程y″＋p（x）y′＋q（x）y＝0的解，且二者线性无关，故y″＋p（x）y′＋q（x）y＝0的通解为c₁（y₁－y₃）＋c₂（y₂－y₃），其中c₁，c₂为任意常数。故方程y″＋p（x）y′＋q（x）y＝f（x）的通解为c₁（y₁－y₃）＋c₂（y₂－y₃）＋y₃，即c₁y₁＋c₂y₂＋（1－c₁－c₂）y₃。
第11题：

单选题
函数y＝x3－3x的极大值点是（　　），极大值是（　　）。
A
x＝2；y＝2
B
x＝1；y＝－2
C
x＝－2；y＝－2
D
x＝－1；y＝2

正确答案： B
解析：
将y＝x³－3x两边对x求导，得y′＝3x²－3，令y′＝0得x＝±1；y″（－1）＝－6＜0，则极大值点是x＝－1，此时y＝2。
第12题：

单选题
函数y1（x）、y2（x）是微分方程y′＋p（x）y＝0的两个不同特解，则该方程的通解为（　　）。
A
y＝c₁y₁＋c₂y₂
B
y＝y₁＋cy₂
C
y＝y₁＋c（y₁＋y₂）
D
y＝c（y₁－y₂）

正确答案： B
解析：
由解的结构可知，y₁－y₂是该方程的一个非零特解，则方程的通解为y＝c（y₁－y₂）。
第13题：

若y2(x)是线性非齐次方程y'+ P(x)y=Q(x)的解，y1(x)是对应的齐次方程y'+ P(x)y=0的解，则下列函数中哪一个是y'+ P(x)y=Q(x)的解？
A. y=cy1(x)+y2(x) B. y=y1(x)+c2y2(x)
C. y=c[y1(x)+y2(x)] D. y=cy1(x)-y2(x)

答案：A
解析：
提示:由一阶线性非齐次方程通解的结构确定，即由对应齐次方程的通解加上非齐次的一特解组成。
第14题：

设函数y=sin(2x+1)，则y"=_____．

答案：
解析：
填-4sin(2x+1)．
第15题：

设随机变量X～N(0，1)，Y～N(1，4)，且相关系数ρXY=1，则

A.AP{Y=-2X-1}=1
B.P{Y=2X-1}=1
C.P{Y=-2X+1}=1
D.P{Y=2X+1}=1

答案：D
解析：
由相关系数的性质可知：如果|ρXY|=1，则必有P{Y=aX+b}=1，(a≠0)，现在题设条件ρXY=1，只要在P{Y=±2X±1}=1四个选项中选一就可以了，实际上只要确定它们的正负号即可，本题可以从X～N(0，1)和Y～N(1，4)及ρXY=1直接推出P{Y=aX+b}=1中的a，b值.但更方便的，不如直接定出a，b的正负号更简单.
【求解】先来确定常数b，由P{Y=aX+b}=1.可得到E(Y)=aE(X)+b再因为X～N(0，1)，Y～N(1，4)，所以，1=a?0+b，即得b=1现来求常数a，实际上只要判定a的正负号就可以了.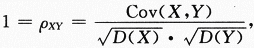

而Cov(X,Y)=Cov(X,aX+b)=aCov(X,X)=a故a>0.答案应选(D).
【评注】从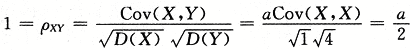，也可得到a=2
第16题：

由函数y=ex的图象与y=-2x，x=1，x=3所围成的封闭面积为_______。

答案：
解析：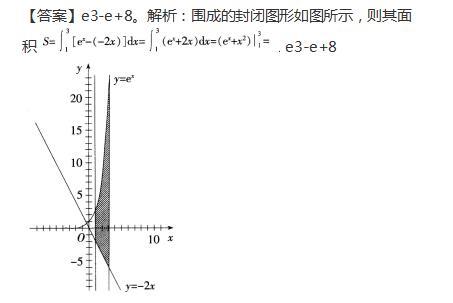
第17题：

线性无关的函数y₁（x），y₂（x），y₃（x）都是二阶非齐线性方程y"+a₁（x）y’+a₂（x）y=f（x）的解。C₁，C₂是任意常数，则该方程的通解是（）。
- A、y=C₁y₁+C₂y₂+y₃
- B、y=C₁y₁+C₂y₂+（C₁+C₂）y₃
- C、y=C₁y₁+C₂y₂-（1-C₁-C₂）y₃
- D、y=C₁y₁+C₂y₂+（1-C₁-C₂）y₃
正确答案:D
第18题：

设X~N（0，1），Y=2X+1，则P{Y-1∣<2}=（）

正确答案:2Φ（1）-1或0.7
第19题：

填空题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

正确答案： -1/7
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第20题：

单选题
已知函数的全微分df（x，y）＝（3x2＋4xy－y2＋1）dx＋（2x2－2xy＋3y2－1）dy，则f（x，y）等于（　　）。
A
x³＋2x²y－xy²＋y³＋x－y＋C
B
x³－2x²y＋xy²－y³＋x－y＋C
C
x³＋2x²y－xy²＋y³－x＋y＋C
D
x³＋2xy²－xy²＋y³＋x－y＋C

正确答案： B
解析：
由题意知∂f/∂x＝3x²＋4xy－y²＋1，两边对x求积分，则f＝∫（∂f/∂x）dx＝x³＋2x²y－xy²＋x＋C（y），∂f/∂y＝2x²－2xy＋C′（y），又因为∂f/∂y＝2x²－2xy＋3y²－1，故C′（y）＝3y²－1，进而有C（y）＝y³－y＋C，f＝x³＋2x²y－xy²＋y³＋x－y＋C。故应选（A）。
第21题：

单选题
设随机变量X～N（0，1），Y～N（0，4），且相关系数ρXY=1，则（　　）.
A
P{Y=-2X-1}=1
B
P{Y=2X-1}=1
C
P{Y=-2X+1}=1
D
P{Y=2X+1}=1

正确答案： B
解析：
令Y=aX+b，因为X～N（0，1），Y～N（1，4），则EY=aEX+b=1，得b=1，
D（Y）=a2D2（X）=4，则a=±2.
又ρXY=1，则a＞0，故a=2.
故应选D.
第22题：

单选题
设y1＝e2x/2，y2＝exshx，y3＝exchx，则（　　）。
A
y₁，y₂，y₃都没有相同的原函数
B
y₂与y₃有相同的原函数，但与y₁的原函数不相同
C
y₁，y₂，y₃有相同的原函数e^x/（chx＋shx）
D
y₁，y₂，y₃有相同的原函数e^x/（chx－shx）

正确答案： B
解析：
由于y₁＝e^2x/2，y₂＝（e^2x/2）－1/2，y₃＝（e^2x/2）＋1/2，故三个函数的原函数都不相同。
第23题：

单选题
设线性无关函数y1、y2、y3都是二阶非齐次线性方程y″+P（x）y′+Q（x）y=f（x）的解，C1、C2是待定常数。则此方程的通解是：（）
A
C₁y₁+C₂y₂+y₃
B
C₁y₁+C₂y₂-（C₁+C₃）y₃
C
C₁y₁+C₂y₂-（1-C₁-C₂）y₃
D
C₁y₁+C₂y₂+（1-C₁-C₂）y₃

正确答案： D
解析：暂无解析

11 、点 A （ 2 ， y 1 ） 、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ） ．

题目

相似考题

参考答案和解析

更多“11 、点 A ( 2 , y 1 ) 、 B ( 3 , y 2 )是二次函数 y=x 2－ 2x＋1 的图象上两点,则 y 1 与 y 2 的大 ”相关问题

相关内容

11 、点 A （ 2 ， y 1 ）、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ）．