12 、现有两个不透明的袋子，其中一个装有标号分别为 1 、 2 的两个小球，另一个装有标号分别为 2 、 3 、 4 的三个小球，小球除标号外其它均相同，从两个袋子中各随机摸出 1 个小球，两球标号恰好相同的概率是 _________ ．

题目

相似考题

1.（本小题8分）有3个完全相同的小球，把它们分别标号为1，2，3，放在一个口袋中，随机地摸出一个小球不放回，再随机地摸出一个小球．（Ⅰ）采用树形图法（或列表法）列出两次摸球出现的所有可能结果；（Ⅱ）求摸出的两个球号码之和等于5的概率．

2.从甲袋内摸出一个白球的概率是1/3,从乙袋内摸出一个白球的概率是1/2,从两个袋内各摸出一个球,那么________等于1/6。A．2个球都是白球的概率B．2个球都不是白球的概率C．2个球不都是白球的概率D．2个球中恰有1个白球的概率

3.一个袋子里装了各种颜色的小球，其中红球个数占1/4，后来又向袋子中放入10个红球，这时红球个数占总数的2/3，问原来袋子中共有多少球?

4.在一个不透明的布袋中装有2个白球和n个黄球，它们除颜色不同外，其余均相同，若从中随机摸出一球，摸到黄球的概率是4/5 ，则n=__________________.

更多“12 、现有两个不透明的袋子，其中一个装有标号分别为 1 、 2 的两个小球，另一个装有标号分别为 2 、 3 、 4 的三个小球，小球除标号外其它均相同，从两个袋子中各随机摸出 1 个小球，两球标号恰好相同的概率是 _________ ．”相关问题

第1题：

一个袋子里放着各种颜色的小球，其中红球占 1/4。后来又往袋子里放了 10 个红球，这时红球占总数的 2/3，问原来袋子里有球多少个？( )
A.8
B.6
C.4
D.2

正确答案：A
第2题：

一个袋子里装有三种不同颜色但大小相同的小球。红色小球上标有数字1，黄色小球上标有数字2，蓝色小球上标有数字3。小明从袋中摸出10个小球，它们的数字和是21，那么小明摸出的小球中最多可能有多少个小球是红色的?（）
A．3个
B．4个
C．5个
D．6个

正确答案：B
第3题：

一个不透明的袋子中装有3个分别标有数字3，1，-2的球，从中随机摸出两个球，则这两个球上数字之和为负数的概率为( )。

A.1/6
B.1/3
C.1/2
D.2/3

答案：B
解析：
三个数取两数随机组合有三种情况，数字之和分别为4、1、-1，则两个球上数字之和为负数的概率为1/3
第4题：

一个布袋中装有大小相同的3个白球、4个红球和2个黑球，每次从袋中摸出一球不再放回。问恰好在第3次取得黑球的概率是多少？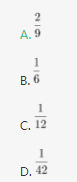

答案：A
解析：
第5题：

有白球和黑球各3个且白球和黑球中各有两个球分别印有1、2两个号码。现将这6个球放入袋子里，充分搅匀后有放回地每次摸取一个球，则前两次恰好摸到同编号的异色球的概率为（）。

答案：D
解析：
第一次取到有编号的球的概率为，假设取到白色1号球，则第二次必须取到黑色1号球，其概率为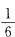。因此前两次恰好摸到同编号的异色球的概率为。。
第6题：

一个袋子里放有10个小球(其中4个白球，6个黑球)，无放回地每次抽取1个，则第二次取到白球的概率是（）

A. 2/15
B. 4/15
C. 1/5
D. 2/5

答案：D
解析：
解题指导：第一次取到白球，第二次取到白球的机率为4/10*3/9=2/15 ；第一次取到黑球，第二次取到白球的机率为6/10*4/9=4/15 。可知，第二次取到白球的机率为4/15+2/15=2/5,故答案为D。
第7题：

有白球和黑球各3个且白球和黑球中各有两个球分别印有1、2两个号码。现将这6个球放入袋子里，充分搅匀后有放回地每次摸取一个球，则前两次恰好摸到同编号的异色球的概率为（）。
A. 4/9 B. 4/15 C. 2/9 D.1/9

答案：D
解析：
D [解析]第一次取到有编号的球的概率为2/3，假设取到白色1号球，则第二次必须取到黑色1号球，其概率为1/6。因此前两次恰好摸到同编号的异色球的概率为2/3 X 1/6 = 1/9。
第8题：

一个袋中装有形状大小完全相同，编号分别为1，2，3，4，5，6的六个球，现从口袋中任取两个球，则至少取到一个编号为质数的球的概率是( )。

A.14/15
B.4/5
C.3/5
D.1/2

答案：B
解析：
第9题：

布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球的概率是。（）
- A、1/5
- B、1/6
- C、1/2
- D、1/3。
正确答案:D
第10题：

从离地面高度相同的同一点，同时以大小相同的速度，水平和竖直向上抛出两个质量相同的小球，运动过程中只受重力。下列说法中正确的是（）
- A、两个小球在空中的运动时间相同
- B、两个小球落地时的速度相同
- C、两个小球在空中的运动过程中，合外力做功相同
- D、两个小球落地时的重力做功的功率相同
正确答案:C
第11题：

单选题
一个口袋内装有5个小球，另一个口袋内装有4个小球，所有这些小球的颜色互不相同．从两个口袋内任取一个小球，不同的取法有（　　）．
A
20种
B
9种
C
5种
D
4种

正确答案： D
解析：
本题为组合问题，共有5＋4＝9种不同的取法．
第12题：

单选题
袋子中装有4个黑球和2个白球，这些球的形状、大小、质地等完全相同，在看不到球的条件下，随机地从袋子中摸出三个球．下列事件是必然事件的是（　　）．
A
摸出的三个球中至少有一个球是黑球
B
摸出的三个球中至少有一个球是白球
C
摸出的三个球中至少有两个球是黑球
D
摸出的三个球中至少有两个球是白球

正确答案： A
解析：
因为白球只有2个，所以，摸出三个球中，黑球至少有一个．
第13题：

一个袋子里放着各种颜色的小球，其中红球占1/4，后来又往袋子里放了10个红球，这时红球占总数的2/3，问原来袋子里有多少个球？（）
A．8
B．12
C．16
D．20

正确答案：A
设原来有小球a个，则有：（a/4+10）÷（a+10）=2/3，解得a=8，选A。
第14题：

在一个袋中，装有五个除数字外其他完全相同的小球，球面上分别标有1、2、3、4、5这5个数字，从中任摸一个球，球面数字是奇数的概率是________．

答案：
解析：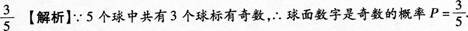
第15题：

一个袋子里放着各种颜色的小球，其中红球占1/4，后来又往袋子里放了10个红球，这时红球占总数的2/3，问原来袋子里有多少个球？（）

A. 8
B. 12
C. 16
D. 20

答案：A
解析：
解题指导：设原来袋中有X个球，则一开始红球有1/4X个，根据题意可得方程1/4X+10=2/3（X+10），解得X=8，故答案选A。
第16题：

一个袋子里有10个小球，其中4个白球，6个黑球，无放回地每次抽取1个，则第二次取到白球的概率是多少？（）

答案：D
解析：
第17题：

袋子里装有红、蓝两色的小球各12个，先从袋子中拿出一个球，然后将它放回袋子中，混合后再从中拿出一个小球。那么两次抽中不同颜色的小球的几率有（）。

A. 20%
B. 25%
C. 50%
D. 60%

答案：C
解析：
第18题：

甲袋内有2个白球3个黑球，乙袋内有3个白球1个黑球，现从两个袋内各摸出1个球，摸出的两个球都是白球的概率是( )

答案：C
解析：
【考情点拨】本题主要考查的知识点为相互独立事件同时发生的概率．【应试指导】由已知条件可知此题属于相互独立同时发生的事件，从甲袋内摸到白球的概率
第19题：

袋子里有50个乒乓球，其中20个黄球，30个白球。现在两个人依次不放回地从袋子中取出一个球，第二个人取出黄球的概率是（）。

A.1/5
B.3/5
C.2/5
D.4/5

答案：C
解析：
第二个人取出黄球的概率是2/5*19/49+3/5*20/49=2/5。
第20题：

一个盒子内装有大小、形状相同的四个球，其中红球1个、绿球1个、白球2个，小明摸出一个球不放回，再摸出一个球，则两次都摸到白球的概率是__________。

答案：
解析：
第21题：

用于地脚灌注的混凝土，其标号与基础混凝土的标号相比要（）
- A、低一个标号
- B、相同
- C、高一个标号
- D、高两个标号
正确答案:C
第22题：

有红，黄，蓝三种颜色的小球各20个，装在一只不透光的袋子里，小李伸手进袋子里面每次任意摸出一个小球。为了保证摸出三个颜色相同的小球，小李应至少摸几次？（）
- A、9
- B、8
- C、7
- D、6
正确答案:C
第23题：

单选题
将号码分别为1、2、…6的6个小球放入一个袋中，这些小球仅号码不同，其余完全相同。首先，从袋中摸出一个球，号码为A.；放回后，再从此袋再摸出一个球，其号码为B.，则使不等式A.-2B.+2>0成立的事件发生的概率为：
A
1/6
B
1/4
C
1/3
D
1/2

正确答案： C
解析：

题目

相似考题

相关内容