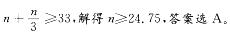(2)估计该校所有班级每周(以5天计)购买饮料的瓶数;
题目
(2)估计该校所有班级每周(以5天计)购买饮料的瓶数;
相似考题
更多“(2)估计该校所有班级每周(以5天计)购买饮料的瓶数; ”相关问题
-
第1题:
某商店售卖可乐、雪碧两种饮料,已知可乐的数量占所有饮料的4/9,商店再次进货20瓶可乐,则可乐的数量占所有饮料的9/19。问:原来商店中的饮料共有多少瓶?A.190
B.250
C.360
D.450答案:C解析:已知可乐的数量占所有饮料的4/9,则商店中的饮料总数应是9的整数倍,可首先排除A、B。根据第二个条件,原饮料总数加上20应该是19的整数倍,排除D,故本题选C。 -
第2题:
一瓶碳酸饮料,一次喝掉饮料1/3后,连瓶共重600克;如果喝掉饮料1/2后,连瓶共重500克;如果只喝掉饮料1/4后,那么连瓶共重多少克?A. 620
B. 650
C. 666
D. 680答案:B解析:设饮料重X,瓶子重Y,则2/3X+Y=600,1/2X+Y=500,X=600,Y=200,则之和掉1/4时,重量为:3/4×600+200=650,故答案为B。 -
第3题:
小李第一次买了A、B、C三种饮料各若干瓶,共花去了75元;之后他再次买了这三种饮料若干瓶,共花去了134元。两次购买的每种饮料数量之和相同,那么若三种饮料各买1瓶最多需花费 ()元。(假设饮料价格都是整数元)A.11
B.15
C.19
D.23答案:C解析:第一步,本题考查约数倍数问题。
第二步,根据条件可知,两次购买饮料的总花费为75+134=209(元),且每种饮料的数量相同,由于总花费=三种饮料各买的瓶数×三种饮料各买1瓶的钱数,故将209分解质因数,209=11×19,可得三种饮料都各买了11瓶时,三种饮料各一瓶的总费用最大,为19元,
因此,选择C选项。 -
第4题:
小李第一次买了A、B、C三种饮料各若干瓶,共花去了75元;之后他再次买了这三种饮料若干瓶,共花去了134元。两次购买的每种饮料数量之和相同,那么若三种饮料各买1瓶最多需花费 元。(假设饮料价格都是整数元)A.11
B.15
C.19
D.23答案:C解析:第一步,本题考查约数倍数问题。
第二步,根据条件可知,两次购买饮料的总花费为75+134=209(元),且每种饮料的数量相同,由于总花费=三种饮料各买的瓶数×三种饮料各买1瓶的钱数,故将209分解质因数,209=11×19,可得三种饮料都各买了11瓶时,三种饮料各一瓶的总费用最大,为19元,
因此,选择C选项。 -
第5题:
某品牌饮料为推广产品推出积拉环赠饮计划,规定收集4个同一容积罐装产品的拉环可以换任意一种口味相同容积的罐装饮料一瓶,已知甲共喝了33瓶饮料,问甲至少购买了多少瓶?( )A. 25
B. 26
C. 27
D. 28答案:A解析:这里拉环相当于空瓶换酒中的瓶,按照空瓶换酒的公式,4瓶=1瓶+ 1酒,即有3瓶=1酒,假设甲购买了 n瓶饮料,则有