f[f(x)]=x4-6x2+6，则f(x)为（ ）A．f(x)=x2-3B．f(x)=x2-12C．f(x)=x2+6D．f(x)=x2-6
题目
f[f(x)]=x4-6x2+6，则f(x)为（ ）
A．f(x)=x2-3
B．f(x)=x2-12
C．f(x)=x2+6
D．f(x)=x2-6
相似考题
更多“f[f(x)]=x4-6x2+6，则f(x)为（ ）A．f(x)=x2-3B．f(x)=x2-12C．f(x)=x2+6D．f(x)=x2-6”相关问题
-
第1题：
若f'(x)＜0(a＜x≤b)且f(b)＞0，则在(a，b)内必有（）A.f(x)＞0
B.f（x)＜0
C.f(x)＝0
D.f(x)符号不定答案：A解析：因为f'(x)＜0x∈(a，b)，所以f(x)单调减少x∈(a，b)．
又f(b)＞0，所以f(x)＞0x∈(a，b)． -
第2题：
如果∫df（x）=∫dg（x），则下列各式中哪一个不一定成立？A.f（x）=g（x）
B.f'（x）=g'（x）
C.df（x）=dg（x）
D.d∫f'（x）dx=d∫g'（x）dx答案：A解析：提示：举例，设f（x）=x2，g（x）=x2+2，df（x）=2xdx，dg（x）=2xdx，∫df（x）=∫dg（x），但f（x）≠g（x）。 -
第3题：
已知函数f(x)=cos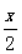
，则下列等式中对于任意x都成立的是（）A.f(x+2π)=f(x)
B.f(π-x)=f(x)
C.f(-x)=f(x)
D.f(-x)=-f(x)答案：C解析： -
第4题：
假设随机变量X的分布函数为F（x），密度函数为f（x）.若X与-X有相同的分布函数，则下列各式中正确的是（ ）《》（ ）A.F（x）=F（-x）；
B.F（x）=-F（-x）；
C.f（x）=f（-x）；
D.f（x）=-f（-x）.答案：C解析： -
第5题：
若f（-x）=f（x），且在（0，+∞）内f′（x）＞0，f″（x）＜0，则f（x）在（-∞，0）内（ ）。《》（ ）A.f′（x）＜0，f″（x）＜0
B.f′（x）＜0，f″（x）＞0
C.f′（x）＞0，f″（x）＜0
D.f′（x）＞0，f″（x）＞0答案：A解析：已知在给出的（0，+∞）内，f′（x）＞0，f″（x）＜0，故在（0，+∞）上f（x）单调递增，且图形是凸的，再根据已知条件f（-x）=f（x）可知f（x）是偶函数，利用图形的对称性可得出f（x）在（-∞，0）是单调递减且也是凸的。故应该选择A。 -
第6题：
A.f(-x，y)=f(x，y)，f(x，-y)=-f(x，y)
B.f(-x，y)=f(x，y)，f(x，-y)=f(x，y)
C.f(-x，y)=-f(x，y)，f(x，-y)=-f(x，y)
D.f(-x，y)=-f(x，y)，f(x，-y)=f(x，y)答案：B解析：要求f(x，y)关于x和y都是偶函数。 -
第7题：
若在区间(a，b)内，f′(x)=g′(x)则下列等式中错误的是( )。A.f(x)=cg(x)
B.f(x)=g(x)+c
C.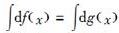
D.df(x)=dg(x)答案：A解析：A项，两边同时求导得f′(x)=cg′(x)，与题意不符。 -
第8题：
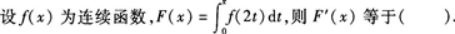A.f(2x)
B.2f(x)
C.f(-2x)
D.-2f(x)答案：A解析：由可变上限积分求导公式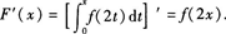
可知因此选A． -
第9题：
奇函数f（x）在闭区间[-1，1]上可导，且f′（x）≤M（M为正常数），则必有（ ）《》（ ）A.f（x）≥M
B.f（x）＞M
C.f（x）≤M
D.f（x）＜M答案：C解析：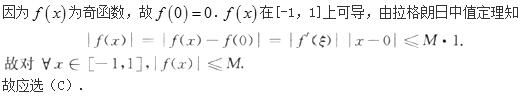
-
第10题：
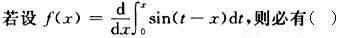A.f（x）=-sinx
B.f（x）=-1+cosx
C.f（x）=1+cosx
D.f（x）=1-sinx答案：A解析：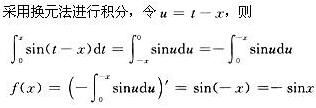
-
第11题：
若f（x）=-f（-x），在（0，+∞）内f′（x）＞0，f″（x）＞0，则在（-∞，0）内（ ）《》（ ）A.f′（x）＜f″（x）＜0
B.f′（x）＜f″（x）＞0
C.f′（x）＞f″（x）＜0
D.f′（x）＞f″（x）＞0答案：C解析：
-
第12题：
若f(x)、F(x)分别为随机变量X的密度函数、分布函数，则( )。A.F(x)=f(x)
B.F(x)≥f(x)
C.F(x)≤f(x)
D.f(x)=-F＇(x)答案：D解析：
-
第13题：
设F（x）是f（x）的一个原函数，则∫e-x f（e-x ）dx等于下列哪一个函数？A.F（e-x）+c
B.-F（e-x）+c
C.F（ex）+c
D.-F（ex）+c答案：B解析：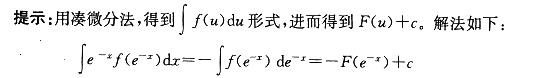
-
第14题：
设函数f(x)＝ex，则．f(x－a)·f(x＋a)＝（ ）A.f(x2－a2)
B.2f(x)
C.f(x2)
D.f2(x)答案：D解析：
-
第15题：
若在区间(a,b)内，f'(x)=g'(x)，则下列等式中错误的是：A.f(x)=cg(x)
B.f(x)=g(x)+c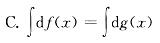
D. df(x)=dg(x)答案：A解析：提示 对A求导，得f'(x)=cg'(x)。 -
第16题：
设f（x）是定义在[-a，a]上的任意函数，则下列答案中哪个函数不是偶函数？A.f（x）+f（-x）
B.f（x）*f（-x）
C.[f（x）]2
D.f（x2）答案：C解析：提示：利用函数的奇偶性定义来判定。选项A、B、D均满足定义F（-x）=F（x），所以为偶函数，而C不满足，设F（x）= [f（x）]2，F（-x）= [f（-x）]2，因为f（x）是定义在 [-a,a]上的任意函数，f（x）可以是奇函数，也可以是偶函数，也可以是非奇非偶函数，从而推不出F（-x）=F（x）或 F（-x） = -F（x）。 -
第17题：
设连续型随机变量X的密度函数为f(x),分布函数为F(x).如果随机变量X与-X分布函数相同,则().
A.F(z)=F（-x）
B.F(x)=F（-x）
C.F(X)=F（-x）
D.f(x)=f（-x）答案：C解析：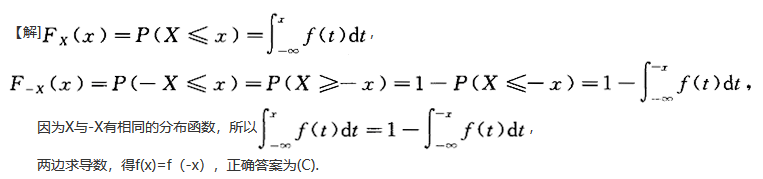
-
第18题：
设y=f(t)，t=φ(x)都可微，则dy=( )。A.f′(t)dt
B.φ′(x)dx
C.f′(t)φ′(x)dt
D.f′(t)dx答案：A解析：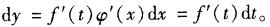
-
第19题：
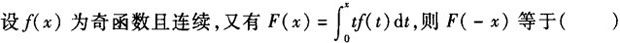A.F（x）
B.-F（x）
C.0
D.2F（x）答案：B解析： -
第20题：
A.f(x)
B.f(x)+C
C.f/(x)
D.f/(x)+C答案：A解析：由不定积分的性质“先积分后求导，作用抵消”可知应选A． -
第21题：
设函数f（x），g（x）是大于零的可导函数，且f′（x）g（x）-f（x）g′（x）＜0，则当a＜x＜b时有（ ）《》（ ）A.f（x）g（b）＞f（b）g（x）
B.f（x）g（a）＞f（a）g（x）
C.f（x）g（x）＞f（b）g（b）
D.f（x）g（x）＞f（a）g（a）答案：A解析：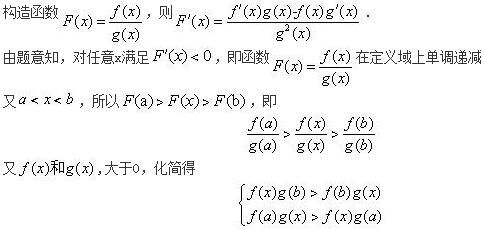
-
第22题：
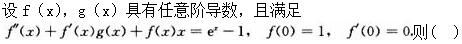A.f（0）=1为f（x）的极小值
B.f（0）=1为f（x）的极大值
C.f（x），f（0）为曲线y=f（x）的拐点
D.由g（x）才能确定f（x）的极值或拐点答案：A解析： -
第23题：
设函数y=f(x)为最小正周期为π的奇函数，则f(x)可能是( )。A.f(x)=sinx
B.f(x)=tan2x
C.f(x)=sin(2x+π/2)
D.f(x)=sinxcosx答案：D解析：