设f为从集合X到集合Y的映射，f:X-＞Y，其中X={1,2,3},Y={4,5,6}, f（1)=4, f（2)=5,f（3)=5,则f是双射。

题目

相似考题

1.有以下程序A： int f1(int x，int y) { return x＞y?x:y; } int f2(int x,int y) { return x＞y?y:x; ) main() { int a=4,b=3,c=5,d=2,e,f,g; e=f2(f1(a,B),f1(c,D));f=f1(f2(a,B),f2(c,D)); g=a+b+c+d-e-f; printf("%d,%d,%d\n",e,f,g)； } 程序运行后的输出结果是( )。A．4,3,7B．3,4,7C．5,2,7D．2,5,7

2.有以下程序 int f1(int x,int y){return x＞y?x：y； } int f2(int x,int y){return x＞y?y：x； } main() { int a=4,b=3,c=5，d=2，e，f，g； e=f2(f1(a，b)，n(c，d))；f=f1(f2(a，b)，n(c，d))； g=a+b+c+d-e-f； printf("%d，%d，%d\n"，e，f，g)； } 程序运行后的输出结果是______。A．4,3,7B．3,4,7C．5,2,7D．2,5,7

3.有以下程序： int f1(int x, int y){ return x＞y? x:y; } int f2(int x, int y){ return x＞y? y:x; } main() { int a=4, b=3, c=5, d=2, e, f, g; e=f2(f1(a, b), f1(c, d)); f=f1(f2(a, b) , f2(c, d)); g=a+b+c+d-e-f; printf("% d, %d, %d\n", e, f, g); } 程序运行后的输出结果是______。A．4, 3, 7B．3, 4, 7C．5, 2, 7D．2, 5, 7

4.有以下程序: main( ) int f1 (int x, int y) { return x＞y?x:y; } int f2 (int x, int y) { return x＞y?y:x; } main( ) { int a=4,b=3,c=5,d,e,f; d=f1(a,b); d=f1(d,c); e=f2(a,b); e=f2(e,c); f=a+b+c-d-e; printf("%d,%d,%d\n",d,f,e); } 执行后输出的结果是A．3,4,5B．5,3,4C．5,4,3D．3,5,4

更多“设f为从集合X到集合Y的映射，f:X-＞Y，其中X={1,2,3},Y={4,5,6}, f（1)=4, f（2)=5,f（3)=5,则f是双射。”相关问题

第1题：

有以下程序 int f1[int x.int y){ return x＞y?x:y; } int f2(int x, int y){ returrnx＞y?y:x; } main ( ) { int a=4,b=3, c=5, d=2, e, f, g; e = f2(f1(a,b}, f1(c,d)); f=f1(f2(a,b), f2(c,d);; g = a+b+c+d-e-f; printf("%d,%d,%d\n",c,f,g); } 程序运行后的输出结果是
A．4,3,7
B．3,4,7
C．5,2,7
D．2,5,7

正确答案：A
解析：本题考查的是函数的综合应用．程序开头定义了两个函数f1()、f2()，每个函数都只有一条语句，在f1()中是“如果x＞y则返回x否则返回广，即返回两个参数中较大的那一个，C()则正好相反，返回较小的．主函数的语句e=f2(f1(a,b)，f1(c，d))；是使用两次调用n()函数的返回值作为f2()函数的参数，并将n()的返回值赋给变量e．a、b中较大的数是a为4，c．d中较大的数是c为5，4和5中较小的数是4，所以结果e=4．同理可以推出f=3，那么g=a+b+c+d-e-f=4+3+5+2-4-3=7。所以，4个选项中选项A符合题意。
第2题：

有以下程序int f1(int x, int y){ return x＞y? x:y;}int f2(int x, int y){ return x＞y? y:x；}main(){ int a=4,b=3,c=5,d,e,f; d=f1(a,B) ;d=f1(d,C) ; e=f2(a,B) ；e=f2(e,C) ; f=a+b+c-d-e; cout＜＜d＜＜", "＜＜f＜＜", "＜＜e＜＜end1;}执行后输出结果是
A．3,4,5
B．5,3,4
C．5,4,3
D．3,5,4

正确答案：C
解析：本题只需要考生按照执行顺序分析即可得出正确答案为C。
第3题：

有以下程序:include using namespace std;int f1(int x, int y){ return x>y ? x:y;}

有以下程序： #include ＜iostream＞ using namespace std; int f1(int x, int y) { return x＞y ? x:y; } int f2(int x, int y) { return x＞y? y:x; } int main ( ) { int a = 4,b = 3,c = 5,d,e,f; d = f1(a,b) ; d = f1(d,c) ; e = f2 (a,b) ; e = f2(e,c) ; f = a+b+c-d-e; cout＜＜d＜＜", "＜＜e＜＜", "＜＜f＜＜end1; return 0; } 执行后的输出结果是 ( )。
A．3,4,5
B．5,3,4
C．5,4,3
D．3,5,4

正确答案：B
解析：本题考核函数的调用和条件运算符(?)。解此题前，先来复习一下条件运算符的运算规则。对于表达式：表达式1＞?表达式2＞：表达式3＞，它的运算方式为：先计算表达式1的值，如果其值为真(true)，则表达式2的值就是整个表达式的最终结果，否则表达式3的值就是整个表达式的值。在了解条件运算符的运算规则后，来看函数f1()和f2()。根据条件运算符的运算规则，可得到函数f1()的功能是返回两数中的较大值，函数f2()的功能足返回两数中的较小值。再分析主函数，由于a=4，b=3，d经过第1次赋值后得到值为4，即d=4。d的第2次赋值表达式为“d=f1(d，C)”，由于此时d=4、c=5，故经过两次赋值后得到d=5。同样e经过两次赋值后可得e=3。再把a=4、b=3、c=5、d=5、e=3代入表达式f=a+b+c-d-e，最后得到f=4。
第4题：

设f（x）、f'（x）为已知的连续函数，则微分方程y'+ f'（x）y = f（x）f'（x）的通解是：

答案：C
解析：
提示：对关于y、y'的一阶线性方程求通解。其中P（x）=f'（x）、Q（x）=f（x） * f'（x），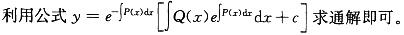
第5题：

设随机变量X，Y独立同分布，且X的分布函数为F(x)，则Z=max{X，Y}的分布函数为

A.AF^2(x)
B.F(x)F(y)
C.1-［1-F(x)］^2
D.［1-F(x)］［1-F(y)］

答案：A
解析：
随机变量Z=max(X，Y)的分布函数Fz(x)应为Fz(x)=P{Z≤x}，由此定义不难推出Fz(x).【求解】故答案应选(A).
【评注】不难验证(B)F(x)F(y)恰是二维随机变量(X，Y)的分布函数.(C)1-［1-F(x)］^2则是随机变量min(X，Y)的分布函数.(D)［1-F(x)］［1-F(y)］本身不是分布函数，因它不满足分布函数的充要条件.
第6题：

判断下列公式是否为可合一，若可合一，则求出其最一般合一。（1）P（a，b），P（x，y）（2）P（f（x），b），P（y，z）（3）P（f（x），y），P（y，f（b））（4）P（f（y），y，x），P（x，f（a），f（b））（5）P（x，y），P（y，x）

正确答案: （1）可合一，其最一般和一为：σ={a/x，b/y}。
（2）可合一，其最一般和一为：σ={y/f（x），b/z}。
（3）可合一，其最一般和一为：σ={fB./y，b/x}。
（4）不可合一。
（5）可合一，其最一般和一为：σ={y/x}。
第7题：

设随机变量X，Y独立同分布，且X的分布函数为F（x），则Z=max{X，Y}的分布函数为（）
- A、F²（x）
- B、F（x）F（y）
- C、1-[1-F（x）]²
- D、[1-F（x）][1-F（y）]
正确答案:A
第8题：

填空题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

正确答案： -1/7
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第9题：

单选题
设z=f（x2+y2），其中f具有二阶导数，则等于（）．
A
2f’（x2+y2）
B
4x2f（x2+y2）
C
2’（x2+y2）+4x2f（x2+y2）
D
2xf（x2+y2）

正确答案： D
解析：暂无解析
第10题：

问答题
判断下列公式是否为可合一，若可合一，则求出其最一般合一。（1）P（a，b），P（x，y）（2）P（f（x），b），P（y，z）（3）P（f（x），y），P（y，f（b））（4）P（f（y），y，x），P（x，f（a），f（b））（5）P（x，y），P（y，x）

正确答案：（1）可合一，其最一般和一为：σ={a/x，b/y}。
（2）可合一，其最一般和一为：σ={y/f（x），b/z}。
（3）可合一，其最一般和一为：σ={fB./y，b/x}。
（4）不可合一。
（5）可合一，其最一般和一为：σ={y/x}。
解析：暂无解析
第11题：

填空题
设f（x，y）＝ax＋by，其中a，b为常数，则f[xy，f（x，y）]＝____。

正确答案： axy+abx+b²y
解析：
由f（x，y）＝ax＋by知，f[xy，f（x，y）]＝axy＋b（ax＋by）＝axy＋abx＋b²y。
第12题：

单选题
设y1（x）是方程y′＋P（x）y＝f1（x）的一个解，y2（x）是方程y′＋P（x）y＝f2（x）的一个解，则y＝y1（x）＋y2（x）是方程（　　）的解。
A
y′＋P（x）y＝f₁（x）＋f₂（x）
B
y＋P（x）y′＝f₁（x）－f₂（x）
C
y＋P（x）y′＝f₁（x）＋f₂（x）
D
y′＋P（x）y＝f₁（x）－f₂（x）

正确答案： A
解析：
根据题意可知，y₁′＋P（x）y₁＝f₁（x），y₂′＋P（x）y₂＝f₂（x）。两式相加得（y₁′＋y₂′）＋P（x）（y₁＋y₂）＝f₁（x）＋f₂（x）。则可发现y＝y₁＋y₂是方程y′＋P（x）y＝f₁（x）＋f₂（x）的解。
第13题：

有以下程序 int f1(int x,int y) { return x＞y?x:y; } int f2(int x,int y) { return x＞y?y:x; } main() { int a=4,b=3,c=5,d,e,f； d=f1(a,b) ； d=f1(d,c) ； e=f2(a,b) ； e=f2(e,c) ； f=a+b+c-d-e； printf("%d,%d,%d\n",d,f,e)； } 执行后输出结果是
A．3,4,5
B．5,3,4
C．5,4,3
D．3,5,4

正确答案：C
解析：函数f1()的作用是返回形参x和y的较大值，函数f2()的作用是返回形参x和y的较小值，在main()函数中通过调用两次f1()函数，求得a、b、c的最大值并存放在变量d中，通过调用两次f2()函数，求得a、b、c的最小值并存放到变量e中。由程序可知d值为5，f的值为4，e的值为3，因此最后输出的d、f、e的值为5、4、3。
第14题：

有以下程序： int f1(int x,int y) { return x＞y?x:y; } int f2(int x，int y) { return x＞y?y:x; } main() { int a=4,b=3,c=5,d,e,f; d=fl(a,b);d=f1(d,c); e=f2(a,b);e=f2(e,c); f=a+b+c-d-e; printf("%d,%d,%d\n",d,f,e); } 执行后输出结果是( )。
A．3,4,5
B．5,3,4
C．5,4,3
D．3,5,4

正确答案：C
解析：函数f1()的作用是返回形参x和y的较大值，函数f2()的作用是返回形参x和y的较小值，在main()函数中通过调用两次f1()函数，求得a、b、c的最大值并存放在变量d中，通过调用两次f2()函数，求得a、b、c的最小值并存放到变量e中。由程序可知d值为5，f的值为4，e的值为3，因此最后输出的d、f、e的值为5、4、3。所以C选项为所选。
第15题：

下列程序的输出结果是( )。 int f1(int x,int y){return x＞y?x:y;} int f2(int x,int y){return x＞y?y:x;} main( ) { int a=4,b=3,c=5,d=2,e,f,g; e=f2(f1 (a,b),f1 (c,d)); f=f1 (f2(a,b),f2(c,d)); g=a+b+c+d-e-f; printf("%d,%d,%d\n,e, f,g); }
A．4,3,7
B．3,4,7
C．5,2,7
D．2,5,7

正确答案：A
解析：根据函数intf1(int,inty){returnx＞y?x:y}和intf2(intx,inty){returnx,＞y?y:x;}的定义可知，如果x＞y成立，则函数n返回x的值，函数f2返回y的值。所以f1(a,b)=4,f1(c,d)=5,f2(a,b)=3,f3(c,d)=2故e=f2(4,5)=4,f=f1(3,2)3,g=4+3+5+2-4-3=7。
第16题：

设f(x),f'(x)为已知的连续函数，则微分方程y'十f'(x)y=f(x)f'(x)的通解是：
A. y=f(x)+ce-f(x) B. y= f(x)ef(x) -ef(x) +c
C. y=f(x)-1+ce-f(x) D. y=f(x)-1+cef(x)

答案：C
解析：
提示:对关于y、y'的一阶线性方程求通解。其中p(x)=f'(x)、Q(x) =f(x)*f'(x) 利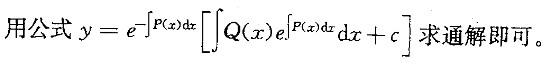
第17题：

仔细阅读下面程序，请给出运行结果（）。#include#includeint f1（int x）{return x*x；}int f2（int x）{return x*x*x；}main（）{int x=3,y1,y2,y3,y4；int（*f）（）；f=f1；y1=（*f）（x）；y2=f1（x）；f=f2；y3=f（x）；y4=f2（x）；printf（“y1=%d，y2=%d，y3=%d，y4=%d\n”，y1，y2，y3，y4）；}

A.y1=9,y2=9,y3=27,y4=27
B.y1=3,y2=9,y3=27,y4=9
C.y1=3,y2=3,y3=9,y4=9
D.y1=3,y2=9,y3=9,y4=27

答案：A
解析：
题中y2和y4是直接函数调用，毫无疑问是9和27，关键在于f=f1是将函数指针f指向了函数f1，因此y1=（*f）（x）本质是调用了函数f1，其结果与直接调用y2=f1（x）相同，y3同理。
第18题：

指出下列关系模式是第几范式？并说明理由。（1）R（X，Y，Z）F＝{XY→Z} （2）R（x，Y，z）F＝{Y→z，XZ→Y} （3）R（X，Y，Z）F＝{Y→Z，Y→X，X→YZ} （4）R（x，Y，z）F＝{X→Y，X→Z} （5）R（x，Y，Z）F＝{XY→Z} （6）R（W，X，Y，Z）F＝{X→Z，WX→Y}

正确答案: （1）R是BCNF。R候选关键字为XY，F中只有一个函数依赖，而该函数依赖的左部包含了R的候选关键字XY。
（2）R是3NF。R候选关键字为XY和XZ，R中所有属性都是主属性，不存在非主属性对的候选关键字的传递依赖。
（3）R是BCNF。R候选关键字为X和Y，∵X→YZ，∴X→Y，X→Z，由于F中有Y→Z，Y→X，因此Z是直接函数依赖于X，而不是传递依赖于X。又∵F的每一函数依赖的左部都包含了任一候选关键字，∴R是BCNF。
（4）R是BCNF。R的候选关键字为X，而且F中每一个函数依赖的左部都包含了候选关键字X。
（5）R是BCNF。R的候选关键字为XY，而且F中函数依赖的左部包含了候选关键字XY。
（6）R是1NF。R的候选关键字为WX，则Y，Z为非主属性，又由于X→Z，因此F中存在非主属性对候选关键字的部分函数依赖。
第19题：

设z=f（x2+y2），其中f具有二阶导数，则等于（）．
- A、2f’（x2+y2）
- B、4x2f"（x2+y2）
- C、2’（x2+y2）+4x2f"（x2+y2）
- D、2xf"（x2+y2）
正确答案:C
第20题：

单选题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
A
1/5
B
1/7
C
－1/7
D
－1/5

正确答案： B
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第21题：

单选题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
A
1
B
－1
C
1/7
D
－1/7

正确答案： B
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|_x_＝0＝f′（4）·4y′|_x_＝0＋f′（2）（1＋y′|_x_＝0），y′|_x_＝0＝4y′|_x_＝0＋（1＋y′|_x_＝0）/2，解得y′|_x_＝0＝－1/7。
第22题：

单选题
设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝（　　）。
A
yf₁′＋f₂′/y－yg′/x²
B
yf₁′－f₂′/y－yg′/x²
C
yf₁′－f₂′/y＋yg′/x²
D
yf₁′＋f₂′/y＋yg′/x²

正确答案： A
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f₁′y＋f₂′·（1/y）＋g′·（－y/x²）＝f₁′y＋f₂′/y－yg′/x²。
第23题：

单选题
若z＝f（x，y）和y＝φ（x）均可微，则dz/dx等于（　　）。[2013年真题]
A
∂f/∂x＋∂f/∂y
B
∂f/∂x＋（∂f/∂y）（dφ/dx）
C
（∂f/∂y）（dφ/dx）
D
∂f/∂x－（∂f/∂y）（dφ/dx）

正确答案： A
解析：
dz/dx＝（∂f/∂x）（dx/dx）＋（∂f/∂y）（dφ/dx）＝∂f/∂x＋（∂f/∂y）（dφ/dx）。
第24题：

单选题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
A
－1/2
B
－1/4
C
－1/7
D
－1/9

正确答案： C
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。

设f为从集合X到集合Y的映射，f:X-＞Y，其中X={1,2,3},Y={4,5,6}, f（1)=4, f（2)=5,f（3)=5,则f是双射。

题目

相似考题

更多“设f为从集合X到集合Y的映射，f:X-＞Y，其中X={1,2,3},Y={4,5,6}, f（1)=4, f（2)=5,f（3)=5,则f是双射。”相关问题

相关内容