一不带电的导体薄球壳半径为R，在球心放一点电荷。如果将此电荷移到R/2处，则移动电荷将改变球壳 电场的分布。（内、外）

题目

一不带电的导体薄球壳半径为R，在球心放一点电荷。如果将此电荷移到R/2处，则移动电荷将改变球壳 电场的分布。（内、外）

相似考题

1.一半径为R的均匀带电球壳,在其球心O处放置一点电荷q,该电荷受的电场力为零,若该电荷偏离球心O,则该电荷q的受力情况为()。A、变大B、变小C、不变D、无法判断

2.已知一带电量为q=10－6C 的点电荷距离不接地金属球壳（其半径R= 5cm）的球心1.5cm处，则球壳表面的最大电场强度Emax为（）。 A. 2.00X104V/m B. 2.46X106V/m C. 3.6X106V/m D. 3.23X106V/m

3.在真空中，半径为R的均匀带电半球面，其面电荷密度为σ，该半球面球心处的电场强度值为（　　）。

4.2)设金属球壳带电量为Q，金属球不带净电荷，求金属球的电势。

更多“一不带电的导体薄球壳半径为R，在球心放一点电荷。如果将此电荷移到R/2处，则移动电荷将改变球壳 电场的分布。（内、外）”相关问题

  • 第1题：

    无限大真空中一半径为a的球，内部均匀分布有体电荷，电荷总量为q。在r a的球外 任一点r处的电场强度的大小E为（）V/m。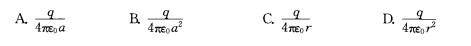


    答案：D
    解析：

  • 第2题：

    无线大真空中有一半径为a的球，内部均匀分布有体电荷，电荷总量为q，在r＜a的球内部，任意－r处电场强度的大小



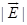
    为（　　）V/m。

    A． qr/（4πε0a）
    B． qr/（4πε0a2）
    C． q/（4πε0r2）
    D． qr/（4πε0a3）

    答案：D
    解析：

  • 第3题：

    在无限大真空中，有一半径为α的导体球，离球心d(d>α)处有一点电荷q ，该导体球的电位ψ应为下列哪项数值？（　　）



    答案：A
    解析：

  • 第4题：

    无限大真空中一半径为a的带电导体球，所带体电荷在球内均匀分布，体电荷总量为q。球外（即r>a处）任一点r处的电场强度的大小E为（　　）V/m。



    答案：D
    解析：
    根据高斯定理，带电金属球在无限大均匀介质中产生的电场呈辐射对称状，半径为r的球面上电场强度大小相等，其值为：

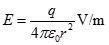
  • 第5题：

    如图4所示，一个未带电的空腔导体球壳，内半径为R，在腔内离球心的距离为d处(d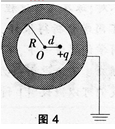


    答案：D
    解析：

  • 第6题：

    在半径为R的球体内，电荷分布是球对称的，电荷体密度为ρ = ar(0≤r≤R)，ρ= 0(r＞R),其中α为大于O的常数，在球体内部，距球心为；x处的电场强度为( )。


    答案：A
    解析：
    。
    提示：作半径为x的同心球面，利用高斯定力可计算出电场强度。

  • 第7题：

    一金属球壳的内、外半径分别为R1和R2，带电荷为Q，在球心处有一电荷为q的点电荷，则球壳内表面上的电荷面密度ρ=（）


    正确答案:-q/（4πR21）

  • 第8题：

    在一不带电荷的导体球壳的球心处放一点电荷，并测量球壳内外的场强分布，如果将此点电荷从球心移到球壳内其它位置，重新测量球壳内外的场强分布，则将发现：（）

    • A、球壳内、外场强分布均无变化
    • B、球壳内场强分布改变，球壳外的不变
    • C、球壳外场强分布改变，球壳内的不变
    • D、球壳内、外场强分布均改变

    正确答案:B

  • 第9题：

    一个半径为R的薄金属球壳，带有电荷q壳内充满相对介电常量为εr的各向同性均匀电介质．设无穷远处为电势零点，则球壳的电势U=（）。


    正确答案:q/（4πε0R）

  • 第10题：

    若在带电的导体球外面同心地罩一均匀介质球壳，则（）。

    • A、导体球的电势将一定升高
    • B、介质球壳内、外壳面极化电荷的电量相等
    • C、导体球的电势将一定降低
    • D、介质球壳内、外表面极化电荷的面密度相等

    正确答案:B

  • 第11题：

    均匀带电球面，球面半径为R，总带电量为q，则球心O处的电场E0=（），球面外距球心r处一点的电场Eφ=（）。


    正确答案:0；q/(4πε0r2)

  • 第12题：

    半径分别R和r的两个球导体（R＞r）相距很远，今用细导线把它们连接起来，使两导体带电，电势为U0，则两球表面的电荷面密度之比σR/σr为（）。

    • A、R/r
    • B、r/R
    • C、R2/r2
    • D、1

    正确答案:B

  • 第13题：

    空气中半径为R的球域内存在电荷体密度ρ＝0.5r的电荷，则空间最大的电场强度值为（　　）。

    A． R2/（8ε0）
    B． R/（8ε0）
    C． R2/（4ε0）
    D． R/（4ε0）

    答案：A
    解析：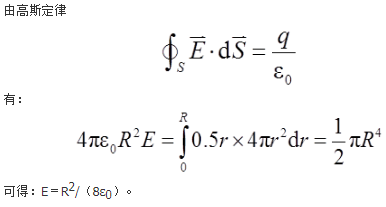

  • 第14题：

    无限大真空中一半径为a的带电导体球，所带体电荷在球内均匀分布，体电荷总量为q。在球外(即r a处)任一点r处的电场强度的大小E为（ ）V/m。


    答案：D
    解析：
    解带电金属球在无限大均匀介质中产生的电场强度E=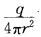V/m。
    答案:D

  • 第15题：

    真空中有一均匀带电球表面，半径为R，电荷总量为q，则球心处的电场强度大小应为下列哪项数值？（　　）



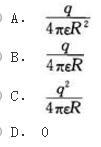    答案：D
    解析：
    带电球体中心场强为0，分析如下取中性点半径为r的小球，其场强为：



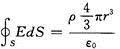
    解得



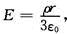
    当 r→0时的极限，即电场强度E=0。
    【说明】根据高斯定理，在任意闭合曲面上，电位移向量的面积积分恒等于该闭合曲面内所有自由电荷的代数和，已知带电球面的自由电荷只是分布在表面，内部没有自由电荷，因此球心处的电场强度为0。这种现象又称为静电屏蔽效应，带电球面的中心处电场强度为0。

  • 第16题：

    一半径为R的半球面，均匀地分布着电荷面密度为盯的电荷，则球心处的电场强度是多少


    答案：
    解析：


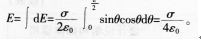
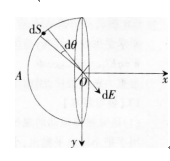
  • 第17题：

    如图所示，一个均匀带电，内、外半径分别为R1和R2的均匀带电球壳，所带电荷体密度为P，A点的电势是（　　）。




    答案：C
    解析：
    空腔内的电势处处相等，因此A点的电势等于球心0点的电势。在半径为r的球壳处取

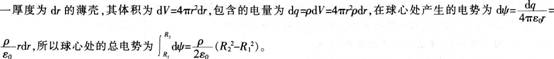
  • 第18题：

    半径为R的均匀带电球面，若其而电荷密度为σ，则在球而外距离球而R处的电场强度大小为（ ）。



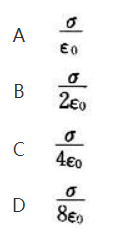    答案：C
    解析：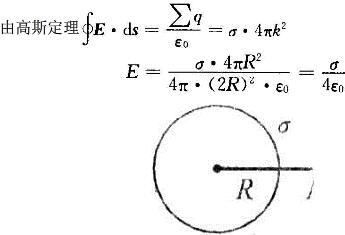

  • 第19题：

    在一不带电荷的导体球壳的球心处放一点电荷，并测量球壳内外的场强分布．如果将此点电荷从球心移到球壳内其它位置，重新测量球壳内外的场强分布，则将发现：（）

    • A、球壳内、外场强分布均无变化.
    • B、球壳内场强分布改变，球壳外不变.
    • C、球壳外场强分布改变，球壳内不变.
    • D、球壳内、外场强分布均改变.

    正确答案:B

  • 第20题：

    带电量Q的导体A置于外半径为R的导体球壳B内，则球壳外离球心r处的电场强度大小（），球壳的电势（）。


    正确答案:E=Q/4πε0r2；V=Q/4πε0R

  • 第21题：

    在一个孤立的导体球壳内，若在偏离球中心处放一个点电荷，则在球壳内、外表面上将出现感应电荷，其分布将是（）

    • A、内表面均匀，外表面也均匀.
    • B、内表面不均匀，外表面均匀.
    • C、内表面均匀，外表面不均匀.
    • D、内表面不均匀，外表面也不均匀.

    正确答案:B

  • 第22题：

    半径为R的不均匀带电球体，电荷体密度分布为ρ=Ar，式中r为离球心的距离（r≤R），A为一常数，则球体中的总电量（）


    正确答案:Q=πAR4

  • 第23题：

    均匀带电球面，电荷面密度为σ，半径为R，球面内任一点的电势为（）。

    • A、不能确定
    • B、与球心处相同
    • C、与球心处不同
    • D、为零

    正确答案:B

  • 第24题：

    在金属球壳外距球心O为d处置一点电荷q，球心O处电势（）。


    正确答案:q/4πεod

相关内容