初等行变换与初等列变换均不改变矩阵的秩.
题目
初等行变换与初等列变换均不改变矩阵的秩.
相似考题
更多“初等行变换与初等列变换均不改变矩阵的秩.”相关问题
-
第1题：
高斯消去法是对增广矩阵(A|b)进行一系列的初等行变换。()此题为判断题(对，错)。
正确答案：正确
-
第2题：
阐述矩阵乘法的运算过程。并用矩阵乘积形式表示如下线性方程组。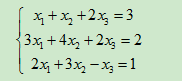
用初等变换的方法求解上述线性方程组。
答案：
-
第3题：
美国初等教育管理与原联邦德国初等学校管理有何异同？
参考答案：美国；
1、学校设置简化；
2、编制灵活；
3）重视教改和实验；
4）创设良好的办学条件和学习环境；
5）争取社会力量办学。
德国：1、学校行政管理简明；
2）教学管理灵活，学习环境优良；
3）家长参与学校管理。
-
第4题：
初等矩阵（ ）A.都可以经过初等变换化为单位矩阵
B.所对应的行列式的值都等于1
C.相乘仍为初等矩阵
D.相加仍为初等矩阵答案：A解析：
-
第5题：
设a为N阶可逆矩阵，则（ ）.
A.若AB=CB，则a=C
B.
C.A总可以经过初等变换化为单位矩阵E
D.以上都不对答案：C解析： -
第6题：
设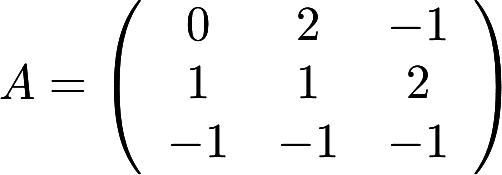
，用初等行变换的方法求A的逆矩阵.然后据此将A分解成初等矩阵的乘积.答案：解析：
-
第7题：
已知a是常数，且矩阵
可经初等列变换化为矩阵.
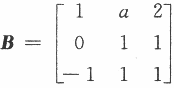
(Ⅰ)求a；
(Ⅱ)求满足AP=B的可逆矩阵P.答案：解析：
-
第8题：
设 A为 n 阶方阵，B是 A 经过若干次初等行变换得到的矩阵，则下列结论正确的是（ ）。A.|A|=|B|
B.|A|≠|B|
C.若|A|=0，则一定有 |B|=0
D.若 |A|＞ 0，则一定有 |B|＞ 0答案：C解析：本题主要考查矩阵的初等变换及行列式的主要性质。对矩阵可以做如下三种变换：（1）对调两行，记作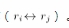
（2）以数 乘某一行的所有元素，记作 。（3）把某一行所有元素的 k 倍加到另一行对应的元素上去，记作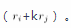
若方阵 A 经过以上三种初等变换得到方阵 B，则对应的行列式的关系依次为 |A|=–|B|，k|A|=|B|，|A|=|B|，即 |A|=a|B|， a∈R （a ≠ 0）。所以 |A|=0 时，必有 |B|=0。C项正确。
A、B、D三项：均为干扰项。与题干不符，排除 -
第9题：
设A为n阶方阵，B是A经过若干次矩阵的初等变换后所得到的矩阵，则有（ ）.《》（ ）
答案：C解析：
-
第10题：
A.A的任意m个列向量必线性无关
B.A的任一个m阶子式不等于0
C.非齐次线性方程组AX=b一定有无穷多组解
D.A通过行初等变换可化为（Em，0）答案：C解析：
-
第11题：
矩阵的初等列变换不包括的形式有（）。
- A、将某一列乘上一个不等于零的系数
- B、将任意两列互换
- C、将某一行乘上一个不等于零的系数再加到另一行上去
- D、将某一列加上一个相同的常数
正确答案:D -
第12题：
单选题设矩阵Am×n的秩r（A）=mAA的任意m个列向量必线性无关
BA的任一个m阶子式不等于0
C非齐次线性方程组AX=b一定有无穷多组解
DA通过行初等变换可化为（Em，0）
正确答案： A解析：
A项和B项，因r（A）=m，则A有m个列向量线性无关或A有m阶子式不为0，但不是任意的；C项，由r（A）=m<n，知方程组AX=b中有n-m个自由未知数，故其有无穷多解；D项，矩阵A仅仅通过初等行变换是不能变换为矩阵（Em，0）的． -
第13题：
阐述求逆矩阵的初等行变换方法。答案及解析:
要求逆的n阶矩阵右边写一个n阶单位阵，然后对这个n×2n阶矩阵按下面程式进行行初等变换（不能作列初等变换）：
将第一行第一列元素化为1，将第一列其余元素化为0；
将第二行第二列元素化为1，将第二列其余元素化为0；
…………
将第n行第n列元素化为1，将第n列其余元素化为0。
这时只要把右边的n阶方阵写下来，就是所要求的逆矩阵。
-
第14题：
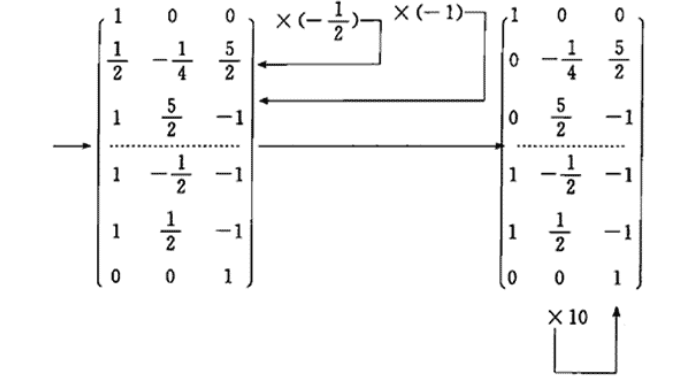
分别用配方法和初等变换法化下列二次型为规范形.
参考答案：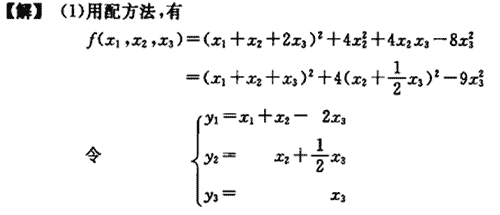
-
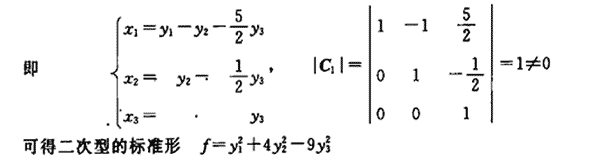
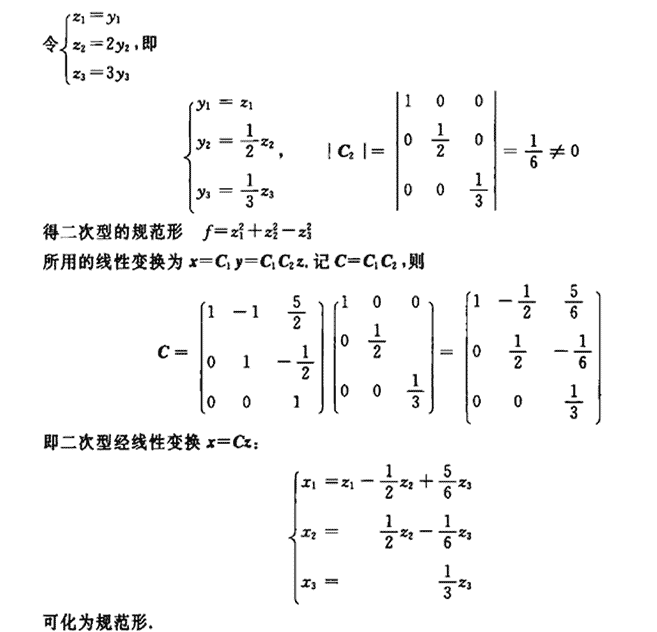
第15题：
矩阵A（ ）时可能改变其秩.A.转置：
B.初等变换：
C.乘以奇异矩阵：
D.乘以非奇异矩阵.答案：A解析： -
第16题：
设a为N阶可逆矩阵，则（ ）.
A.若AB=CB，则a=C：
B.
C.A总可以经过初等变换化为单位矩阵E：
D.以上都不对.答案：C解析： -
第17题：
N阶矩阵A经过若干次初等变换化为矩阵B,则().A.｜A｜=｜B｜
B.｜A｜≠｜B｜
C.若｜A｜=0则｜B｜=0
D.若｜A｜>0则｜B｜>0答案：C解析：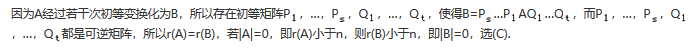
-
第18题：
利用矩阵的初等变换，求方阵
的逆答案：解析：
-
第19题：
设A为m X n矩阵，且r(A)=m小于n，则下列结论正确的是
AA的任意m阶子式都不等于零
BA的任意m个子向量线性无关
C方程组AX=b一定有无数个解
D矩阵A经过初等行变换化为
答案：C解析：
-
第20题：
《普通高中数学课程标准(实验)》中规定的必修课程是每个学生都必须学习的数学内容，列内容不属于必修4的是( )。A、算法初步
B、基本初等函数Ⅱ(三角函数)
C、平面上的向量
D、三角恒等变换答案：A解析：基本初等函数II(三角函数)、平面上的向量、三角恒等变换都属于必修4的内容，算法初步是选修3的内容之一，故选A。 -
第21题：
矩阵A在（ ）时秩改变.A.转置
B.初等变换
C.乘以奇异矩阵
D.乘以非奇异矩阵答案：C解析：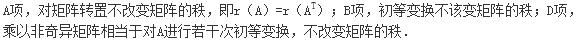
-
第22题：
矩阵的初等行变换不包括的形式有（）。
- A、将某一行乘上一个不等于零的系数
- B、将任意两行互换
- C、将某一行乘上一个不等于零的系数再加到另一行上去
- D、将某一行加上一个相同的常数
正确答案:D -
第23题：
关系中行列次序的变换性质是（）
- A、行可以交换，列不可交换
- B、行不可交换，列可交换
- C、行、列均不可交换
- D、行、列均可以交换
正确答案:D -
第24题：
单选题矩阵A在（ ）时秩改变。A转置
B初等变换
C乘以奇异矩阵
D乘以非奇异矩阵
正确答案： B解析：
A项，对矩阵转置不改变矩阵的秩，即r（A）＝r（AT）；
B项，初等变换不该变矩阵的秩；
D项，乘以非奇异矩阵相当于对A进行若干次初等变换，不改变矩阵的秩。