现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。A、多1个B、少1个C、多2个D、少2个

题目

现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。

  • A、多1个
  • B、少1个
  • C、多2个
  • D、少2个
相似考题

1.甲.乙和丙.丁比赛，甲发球给乙，丙在球着地前触网，然后由于球落在发球区外，判甲发球失误。此题为判断题(对，错)。

2.甲乙丙三名羽毛球选手训练共用了48个羽毛球，其中甲比乙多用了4个，乙比丙多用了4个，他们三人用的羽毛球数之比为（ ）。A．5：4：3B．6：5：4C．4：3：2D．3：2：1

3.有甲，乙三箱水果，甲箱重量与乙，丙两箱重量和之比是1：5，乙箱重量与甲，丙重量之和的比是1：2，甲箱重量与乙箱重量的比是：A.16B.13C.12D.1

4.三个箱子,第一个箱子中有4个黑球2个白球,第二个箱子中有3个黑球5个白球,第三个箱子中有3个黑球2个白球。试求:随机地取一个箱子,再从这个箱子中任取出一球,这个球为白球的概率是多少?

更多“现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。A、多1个B、少1个C、多2个D、少2个”相关问题

  • 第1题：

    甲、乙、丙各有球若干个，甲给乙的球如乙现有的那么多球，甲也给丙如丙现有的那么多球，然后乙也按甲和丙手中球数分别给甲、丙添球，最后丙也按甲和乙手中的球数分别给 甲、乙添球，此时三人都各有16个球，问开始时甲有多少个?（ ） A．26 B．14 C．8 D．10


    正确答案：A
    本题属于复杂的还原问题，要求开始时甲的数量，需要从第三次添球开始向前推。第三次添球后，甲、乙、丙三人手中都是16个球，第三次添球之前甲的球数是16÷2=8个；同样，乙的球数是16÷2=8个；第三次添球前丙的球数是16+8+8=32个；第二次添球之后，甲、乙、丙的球数分别是8，8，32。与上面相似，可以求得第二次添球之前甲的球数是8--2=4个；丙的球数是32"2=16个；乙的球数是8+16+4=28个；第一次添球之后，甲、乙、丙的球数分别为4，28，16。第一次添球前乙的球数是28÷2=14个；丙的球数是16-2=8个；甲的球数是4+14+8=26个；所以，开始时，甲、乙、丙三人手中的球数分别为26、14、8。(注意：倒推是解还原问题的主要方法。对于较复杂的还原问题，还常常根据题目特点，将倒推与其他方法结合起来求解。)故选A。

  • 第2题：

    甲、乙、丙各有球若干个，甲给乙的球等于乙现有的那么多球，甲给丙的球等于丙现有的那么多球，然后乙也按甲和丙手中球数分别给甲、丙添球，最后丙也按甲和乙手中的球数分别给甲、乙添球，此时三人各有16个球，问刚开始时甲有多少个球?（　　）

    A.26　　　　B.14　　　　C.8　　　　D.10


    本题正确答案为A。本题可以使用倒推法求取答案。
    　　由题意知，第三次添球后甲、乙、丙三人手中各有16个球。故在第三次添球前，甲、乙的球为16÷2＝8，而丙的球是16+8+8＝32（个）球。
    　　在第二次添球前，甲的球为8÷2＝4（个），丙为32÷2＝16（个），乙的球数为8+4+16＝28（个）。
    　　第一次添球前，乙的球为28÷2＝14（个），丙的球为16÷2＝8（个），甲的球为4+14+8＝26（个），故A项正确。

  • 第3题：

    甲、乙、丙各有球若干，甲给乙的球和乙现有的球一样多，甲给丙的球和丙现有的球一样多，然后乙也按甲和丙手中的球数分别给甲、丙添球，最后丙也按甲、乙手中的球数分别给甲、乙添球，此时三人都各有球16个，开始时甲有多少个球？（ ）

    A．26

    B．24

    C．32

    D．30


    正确答案：A
    从最后一次开始向前推，第三次，甲有8个，乙有8个，丙有32个，第二次，甲有4个，乙有28个，丙有16个，第一次，甲有26个，乙有14个，丙有8个。

  • 第4题：

    箱子里有红、白两种玻璃球，红球是白球的3倍少2个。每次从箱子里取出7个白球、13个红球，经过若干次后，箱子里剩下6个白球，72个红球，那么，原来箱予里红球比白球多多少个？（ ）

    A．102

    B．104

    C．106

    D．108


    正确答案：D
    D[解析]假设箱子里原来有白球x个，那么红球为（3x-2）个，依题意有（x-6）÷7=（3x-2-72）÷13，解得x=55，所以原来红球比白球多3×55-2-55=108（个）。故选D。

  • 第5题：

    ：有四个外表看起来没有分别的小球，它们的重量可能有所不同。取一个天平，将甲、乙归为一组，丙、丁归为另一组，分别放在天平两边，天平是基本平衡的。将乙、丁对调一下，甲、丁一边明显要比乙、丙一边重得多。可奇怪的是，我们在天平一边放上甲、丙，而另一边则放上乙，还没有来得及放上丁时，天平就压向了乙一边。请你判断，甲球与丁球哪个更重？（ ）

    A．丁球比甲球重

    B．丁球比甲球轻

    C．甲球与丁球同样重

    D．无法确定甲球与丁球的轻重


    正确答案：A
     根据题意，列出甲、乙、丙、丁四个球重量之间的关系。甲+乙＝丙+丁，甲+丁>乙+丙，甲+丙<乙。从这些关系式中可得，甲球比丁球轻，所以选A。

  • 第6题：

    箱子里装满了橡皮球，箱球共重12 千克，从箱中取出1/4 的球后，箱球共重9.5 千克，问箱子重量是（ ）千克？

    A.1
    B.2
    C.0.5
    D.0.3

    答案：B
    解析：
    未取之前，箱球共重12 千克，取出1/4 的球后，箱球共重9. 5 千克，故1/4 的球重2.5 千克，故橡皮球总重10 千克，箱子的重量就是12-10=2 千克。

  • 第7题：

    有甲、乙两个口袋,两袋中都有3个白球2个黑球,现从甲袋中任取一球放入乙袋,再从乙袋中任取4个球,设4个球中的黑球数用X表示,求X的分布律.


    答案：
    解析：

  • 第8题：

    箱子里面有红、白两种玻璃球，红球数比白球数的3倍多两个，每次从箱子里取出7个白球15个红球。如果经过若干次以后，箱子里只剩下3个白球，53个红球，那么，箱子里原有红球比白球多多少个？( )

    A.102
    B.104
    C.106
    D.108

    答案：C
    解析：
    设共取了x次，原有红球(53+15x)个，原有白球(3+7x)个，由题意可得，53+15x=3(3+7x)+2，解得x=7，原有红球比白球多(53+15x)-(3+7x)=106个，

  • 第9题：

    甲、乙、丙分别为红、黄、蓝色的三个小球，放在A、B、C三个箱子里。已知①甲球不是蓝色；②黄色球在A中；③B中的球不是红色的；④乙球不在B中，丙球不在A中。下列推断完全正确的是()。

    A.甲球是红色，在A中
    B.甲球是黄色，在C中
    C.乙球是黄色，在A中
    D.丙球是蓝色，在B中

    答案：D
    解析：
    黄球在A中，B中的球不是红色，则B中球为蓝色，C中球为红色。甲不是蓝色，所以在A或C中，乙球在A或C中。所以，甲在A中、乙在C中，或甲在C中、乙在A中，故丙球在B中。

  • 第10题：

    将10个小球随机放入甲、乙、丙三个盒子中，且每个盒子中小球的个数均为质数，接着在甲、乙、丙三个盒子中分别放入等于其盒内球数的2、3、4倍的小球。两次共放入了39个小球。最终甲盒中的小球比乙盒（）

    • A、多2个
    • B、少11个
    • C、少2个
    • D、少20个

    正确答案:B

  • 第11题：

    单选题
    甲、乙、丙共运来三车苹果，其中甲车比乙车多4箱，乙车比丙车多4箱，甲车比乙车每箱少3个苹果，乙车比丙车每箱少5个苹果，甲车比乙车总共多3个苹果，乙车比丙车总共多5个苹果，这三车苹果共有多少个？
    A

    628

    B

    643

    C

    658

    D

    673


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。
    A

    多1个

    B

    少1个

    C

    多2个

    D

    少2个


    正确答案： B
    解析： 由题知，甲、乙、丙3个箱子里最终的球数为原球数的3、4、5倍，而原来的球数是1或2或3，设三个箱子原来分别有x、y、z个球，则有x+y+x=6……（1），3x+4y+5x=22……（2），因为比较的是甲和乙的关系，因此我们将z消去，用5×（1）-（2）得2x+y=8.如果x=1，y=6，不符合，如果x=2，y=4，不符合，于是x=3，y=2，选A。

  • 第13题：

    有甲、乙、丙三箱水果，甲箱重量与乙、丙两箱重量和之比是1：5，乙箱重量与甲、丙两箱重量之和的比是l：2，甲箱重量与乙箱重量的比是（ ）。

    A．1/6

    B．1/3

    C．1/2

    D．1


    正确答案：C
    设甲、乙、丙三箱水果重分别为x、y、Z，则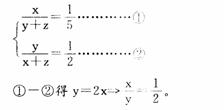

  • 第14题：

    箱子里有红、白两种玻璃球。红球是向球的3倍少2个。每次从箱子里取出7个白球、13个红球，经过若干次后，箱子里剩下6个白球，72个红球，那么，原来箱子里红球比白球多多少个?（ ）

    A．102

    B．104

    C．106

    D．108


    正确答案：D
    假设箱子里原来有白球x个，那么红球为(3x--2)个，依题意有(x－6)÷7=(3x－2－72)÷13，解得x=55，所以原来红球比白球多3×55－2－55=108(个)。故选D。

  • 第15题：

    有甲乙丙三箱水果，甲箱重量与乙、丙两箱重量和之比是1：5，乙箱重量与甲、丙重量之和的比是1：2，甲箱重量与乙箱重量的比是( ) 。

    A.1/6

    B.1/3

    C.1/2

    D.1


    正确答案：C
    【答案】C。解析：设甲，乙，丙箱子重量分别为a,b,c,那么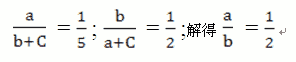

  • 第16题：

    甲乙丙三箱水果，甲与乙的重量之比为3：4，甲与丙的重量之比为5：2，从乙箱取4千克放入丙箱，乙丙重量之比为9：4，则甲、乙、丙三箱重量之和为多少千克? A．40 B．82 C．80 D．70


    正确答案：B
    由题意可知，甲：乙：丙=15：20：6，乙、丙重量比为20：6=10：3。乙丙一共有10+3=13份．置换后重量之比为9：4，依旧是13份。因此乙减少的一份为4千克。所以乙、丙共有13x4=52千克，甲有52÷(20+6)×15=30千克。故共有52+30=82千克。

  • 第17题：

    现有3个箱子，依次放人1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放人其箱内球数的2、3、4倍。两次共放了22个球，最终甲箱中的球比乙箱（）

    A.多1个
    B.少1个
    C.多2个
    D.少2个

    答案：A
    解析：
    三个箱子臞来一共6个球，所以新放进16个，即2甲+3乙+4丙=16,根据奇数偶数的性质，乙是偶数，所以乙是2个球的箱子,所以甲=3,丙=1，因此甲放了9个球，乙放了8个球，多1个。

  • 第18题：

    现有三个箱子,第一个箱子有4个红球,3个白球；第二个箱子有3个红球,3个白球；第三个箱子有3个红球,5个白球；先取一只箱子,再从中取一只球,(1)求取到白球的概率；(2)若取到红球,求红球是从第二个箱子中取出的概率.


    答案：
    解析：

  • 第19题：

    有甲乙丙三箱水果，甲箱重量与乙、丙两箱重量和之比是1：5，乙箱重量与甲、丙重量之和的比是1：2，甲箱重量与乙箱重量的比是( )。

    A. 1：6
    B. 1：3
    C. 1：2
    D. 1：1

    答案：C
    解析：
    设甲，乙，丙箱子重量分别为a,b,c,那么a/b+c=1/5,b/a+c=1/2,a/b=1/2。故答案为C。

  • 第20题：

    将2个红球与1个白球随机地放入甲、乙、丙三个盒子中，则乙盒中至少有1个红球的概率为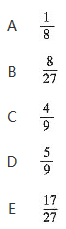


    答案：D
    解析：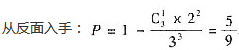

  • 第21题：

    甲/乙与丙/丁比赛，甲发球给丁，丙在球着地前触网，然后由于球落在发球区外，判甲发球失误。


    正确答案:正确

  • 第22题：

    单选题
    将10个小球随机放入甲、乙、丙三个盒子中，且每个盒子中小球的个数均为质数，接着在甲、乙、丙三个盒子中分别放入等于其盒内球数的2、3、4倍的小球。两次共放入了39个小球。最终甲盒中的小球比乙盒（）
    A

    多2个

    B

    少11个

    C

    少2个

    D

    少20个


    正确答案： D
    解析： 不定方程问题。设甲、乙、丙三个盒子中第一次放入小球的个数分别为x、y、z个，由题意列方程得：x+y+z=10，2x+3y+4z=29；消去z后可得：2x+y=11，由于x、y均为质数，易得x=3，y=5，z=2。（x=2，y=7时，z=1，不满足质数的要求。）最后将甲、乙、丙盒子中小球个数代入计算即可。因此，本题答案为B选项。

  • 第23题：

    单选题
    把编号为1-5的球放入编号为1-5的箱子，一个箱子只能放一个，要求第1、5号球放入两个编号相邻的箱子的方法有（）种
    A

    24

    B

    32

    C

    48

    D

    60


    正确答案： B
    解析： 1号5号相邻有4种选择，所以4*A（2，2）*A（3*3）=4*2*6=48种。

相关内容