设域F的单位元e，对任意的n∈N有ne不等于0。

题目

设域F的单位元e，对任意的n∈N有ne不等于0。

相似考题

1.设A是n阶方阵,若对任意的n维向量x均满足Ax=0,则()A、A=0B、A=EC、r(A)=nD、0r(A)(n)

2.下列等式成立的有()。A.(F/A,i,n)=(P/F,i,n)X(A/P,i,n)B.(P/F,i,n)=(A/F,i,n)×(P/A,i,n)C.(A/P,i,n)=(F/P,i,n)×(A/F,i,n)D.(A/P,i,n)=(P/F,i,n1)×(A/F,i,n2),n1+n2=nE.(A/F,i,n)=(P/F,i,n)X(A/P,i,n)

3.设集合N={0，1，2。。。n}，f为N到N 的函数，且f（x）={f(f(+11)) 0<=x<=90x-10 x>90}经计算f(90)=81，f(89)=81,f(49)=_____。

4.设F是一个森林，B是由F变换得的二叉树。若F中有n个非终端结点，则B中右指针域为空的结点有()个A. n-1B. nC. n+1D. n+2

参考答案和解析
正确答案:正确
更多“设域F的单位元e，对任意的n∈N有ne不等于0。”相关问题

  • 第1题：

    设F是一个森林，B是由F转换得到的二叉树，F中有几个非叶结点，则B中右指针域为空的结点有( )个。

    A．n-1

    B．n

    C．n+1

    D．n+2


    正确答案：C
    解析：具体方法是：①将森林中的每棵树变为二叉树。②因为转换所得的二叉树的根结点的右子树均为空，故可将各二叉树的根结点视为兄弟从左至右连在一起，就形成了一棵二叉树。

  • 第2题：

    正态分布计算所依据的重要性质为（ ）。
    A.设X~N(μ,σ2),则μ= (X-μ)/σ~N(0, 1)
    B.设X~N(μ,σ2),则对任意实数a、b有P(XC.设X~N(μ,σ2),则对任意实数a、b有P(X>a) =1-Φ[(a-μ)/σ]
    D.设X~N(μ,σ2),则对任意实数a、b有P(a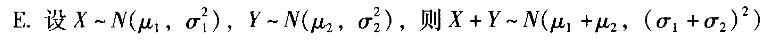


    答案：A,B,C,D
    解析：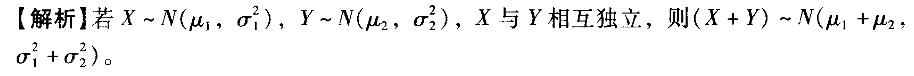

  • 第3题：

    设{an}为数列，对于“存在正数肘，对任意正整数n，有
    的否定(即数列{an}无界)是( )。

    A、存在正数M，存在正整数n，使得|an|＞M
    B、对任意正数M，存在正整数n，使得|an|＞M
    C、存在正数M，对任意正整数n，有|an|＞M
    D、对任意正数M以及任意正整数n，有|an|＞M

    答案：B
    解析：
    对任意正数M，存在正整数n，使得

    则称数列{an}无界．

  • 第4题：

    设F是一个森林，B是由F变换得的二叉树。若F中有n个非终端结点，则B中右指针域为空的结点有（）个。

    • A、n-1
    • B、n
    • C、n+1
    • D、n+2

    正确答案:C

  • 第5题：

    网络的域模式有（）、单主域模式、（）和完全委托域模式。由N个域组成的完全委托域，委托关系有N*（N-1）种。


    正确答案:单域模式；多主域模式

  • 第6题：

    设F是一个有单位元（不为0）的交换环，如果F的每个非零元都是可逆元，那么称F是一个什么？（）

    • A、积
    • B、域
    • C、函数
    • D、元

    正确答案:B

  • 第7题：

    M不能被N整除的FORTRAN表达式为：（）

    • A、（M／N）.NE.0
    • B、NOT.（MOD（M，N）.NE.0）
    • C、MOD（M，N）.NE.0
    • D、INT（M／N）.NE.0

    正确答案:C

  • 第8题：

    单选题
    设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB＝0，则A＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    3


    正确答案： A
    解析：
    取基本单位向量组为ε(→)1，ε(→)2，…，ε(→)n。
    当m＝n时，由对任意B都有AB＝0，则对B＝（ε(→)1，ε(→)2，…，ε(→)n）＝En也成立，即AE＝0，故A＝0。
    当m＞n时，取B＝（ε(→)1，ε(→)2，…，ε(→)n，B(→)1）＝（En，B(→)1），则由AB＝A（En，B(→)1）＝0，知AEn＝0，故A＝0。

  • 第9题：

    填空题
    网络的域模式有（）、单主域模式、（）和完全委托域模式。由N个域组成的完全委托域，委托关系有N*（N-1）种。

    正确答案： 单域模式,多主域模式
    解析： 暂无解析

  • 第10题：

    问答题
    设A为n阶方阵，若对任意n维向量X=（x1，x2，…，xn）T都有AX=0.证明：A=0.

    正确答案：
    证明:由对任意n维向量X都有AX=0,知对基本单位向量组ε1,ε2,…,εn,Aεi=0(i=1,2,…,n)成立.
    所以有A(ε1,ε2,…,εn)=0,即AE=0,故A=0.
    解析： 暂无解析

  • 第11题：

    单选题
    设f（N），g（N）是定义在正数集上的正函数，如果存在正的常数C和自然数N0，使得当N≥N0时有f（N）≤Cg（N），则称函数f（N）当N充分大时有下界g（N），记作f（N）∈○（g（N）），即f（N）的阶（）g（N）的阶。
    A

    不高于

    B

    不低于

    C

    等价于

    D

    逼近


    正确答案： D
    解析： 暂无解析

  • 第12题：

    填空题
    设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB＝0，则A＝____。

    正确答案： 0
    解析：
    取基本单位向量组为ε(→)1，ε(→)2，…，ε(→)n。
    当m＝n时，由对任意B都有AB＝0，则对B＝（ε(→)1，ε(→)2，…，ε(→)n）＝En也成立，即AE＝0，故A＝0。
    当m＞n时，取B＝（ε(→)1，ε(→)2，…，ε(→)n，B(→)1）＝（En，B(→)1），则由AB＝A（En，B(→)1）＝0，知AEn＝0，故A＝0。

  • 第13题：

    正态分布计算所依据的重要性质为( )。

    A．设X～N(μ,σ2)，则u=(X-μ)/σ～N(0，1)

    B．设X～N(μ，σ2)，则对任意实数a、b有P(X＜b)=Ф[(b-μ)/σ)

    C．设X～N(μ，σ2)，则对任意实数a、b有P(X＞a)=1-Ф[(a-μ)/σ]

    D．设X～N(μ，σ2)，则对任意实数a、b有P(a＜X＜b)=Ф[(b-μ)/σ)-Ф[(a-μ)/σ]

    E．设X～μ(μ1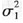，，Y～N(μ2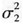，，则X+Y～N(μ1+μ2，(σ1+σ2) 2)


    正确答案：ABCD
    解析：若X～N(μ1，)，Y-N(μ2，)，X与Y相互独立，则(X+Y)～N(μ1，+μ2，+)。

  • 第14题：

    设X～N（μ,σ^2）,其分布函数为F(x),对任意实数a,讨论F(-a)+F(a)与1的大小关系.


    答案：
    解析：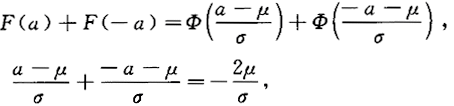

    则μ>0时，F(a)+F（-a）小于1；
    当μ=0时，F(a)+F（-a）=1；
    当μa小于0时，F(a)+F（-a）大于1.

  • 第15题：

    低应变反射波法检测桩身完整性时，设截面上、下的波阻抗比为n，反射系数为F，透射系数为T，则对三者之间的关系表述错误的是（ ）。

    A：n=1时，F=0，T=l
    B：n>1时，F<0，T>0
    C：n<1时，F>0，T>0
    D：n>1时，F>0，T>0

    答案：D
    解析：
    （1）F=（1-n）/（1+n），T=2/（1+n）;（2）当n=1时，F=0，T=l，即桩身无反射波信号，应力波全透射，表示桩身完整。但这-情况在实际检测中曼诸多因素的影响，很难达到，n值只能接近于1。（3）当n>l时，F＜0，T>0，反射波为上行拉力波，与入射波同相，在桩顶检测出的反射波速度和应力与入射波信号极性一致，此时表示桩身有缩径、离析、空洞等。（4）当n＜1时，F>0，T>0，反射波为上行压缩波，在桩顶接收到的反射波速度和应力与入射波信号极性相反，此时表示桩身有扩径、膨胀等病害。

  • 第16题：

    设f（N），g（N）是定义在正数集上的正函数，如果存在正的常数C和自然数N0，使得当N≥N0时有f（N）≤Cg（N），则称函数f（N）当N充分大时有下界g（N），记作f（N）∈○（g（N）），即f（N）的阶（）g（N）的阶。

    • A、不高于
    • B、不低于
    • C、等价于
    • D、逼近

    正确答案:A

  • 第17题：

    在域F中，e是单位元，存在n，n为正整数使得ne=0成立的正整数n是什么？（）

    • A、合数
    • B、素数
    • C、奇数
    • D、偶数

    正确答案:B

  • 第18题：

    记号Ω的定义正确的是（）。

    • A、O（g（n））={f（n）∣存在正常数c和n0使得对所有n≧n0有：0≦f（n）≦cg（n）}
    • B、O（g（n））={f（n）∣存在正常数c和n0使得对所有n≧0有：0≦g（n）≦（n）}
    • C、O（g（n））={f（n）∣对于任何正常数c>0，存在正数和n0>0使得对所有n≧n0有：0≦f（n）<cg（n）}
    • D、O（g（n））={f（n）∣对于任何正常数c>0，存在正数和n0>0使得对所有n≧n0有：0≦cg（n）<f（n）}

    正确答案:B

  • 第19题：

    单选题
    设f（x）在x＝0处满足f′（0）＝f″（0）＝…＝f（n）（0），f（n＋1）（0）＞0，则（　　）。
    A

    当n为偶数时，x＝0是f（x）的极大值点

    B

    当n为偶数时，x＝0是f（x）的极小值点

    C

    当n为奇数时，x＝0是f（x）的极大值点

    D

    当n为奇数时，x＝0是f（x）的极小值点


    正确答案： C
    解析：
    此题可用举例法判断。当n＝1时（即n为奇数），f′（0）＝0，f″（0）＞0。由f″（0）＞0知f′（x）在x＝0处单调增加。又f′（0）＝0，x＜0时f′（x）＜0；x＞0时f′（x）＞0。因此f（x）在x＝0点处取得极小值。
    当n＝2时（即n为偶数），f′（0）＝f″（0）＝0，f‴（0）＞0。由f‴（0）＞0知，f″（x）在x＝0处单调增加。因f″（0）＝0，故f′（x）在x＝0附近先减小后增加。f′（0）＝0，故f（x）在x＝0点处单调。因此x＝0既不是f（x）的极大值也不是它的极小值。综上所述D项正确。

  • 第20题：

    判断题
    设域F的单位元e，对任意的n∈N有ne不等于0。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第21题：

    问答题
    设A为n阶方阵，若对任意n维向量x(→)＝（x1，x2，…，xn）T都有Ax(→)＝0。证明：A＝0。

    正确答案：
    由对任意n维向量x(→)都有Ax(→)=0,知对基本单位向量组ε(→)1,ε(→)2,…,ε(→)n,Aε(→)i=0(i=1,2,…,n)成立。
    所以有A(ε(→)1,ε(→)2,…,ε(→)n)=0,即AE=0,故A=0。
    解析： 暂无解析

  • 第22题：

    单选题
    设f（x）具有任意阶导数，且f′（x）＝[f（x）]2，则f（n）（x）＝（　　）。
    A

    n[f（x）]n＋1

    B

    n![f（x）]n＋1

    C

    （n＋1）[f（x）]n＋1

    D

    （n＋1）![f（x）]n＋1


    正确答案： A
    解析：
    逐次求导：
    f″（x）＝2f（x）f′（x）＝2[f（x）]3
    f‴（x）＝3·2[f（x）]2f′（x）＝3![f（x）]2·[f（x）]2＝3![f（x）]4
    ……
    f（n）（x）＝n![f（x）]n＋1

  • 第23题：

    单选题
    在域F中，e是单位元，存在n，n为正整数使得ne=0成立的正整数n是什么？（）
    A

    合数

    B

    素数

    C

    奇数

    D

    偶数


    正确答案： D
    解析： 暂无解析

相关内容