在R[x]上degf（x）=n>0，若c是它的一个复根，则它的共轭复数也是f（x）的复根。
题目
在R[x]上degf（x）=n>0，若c是它的一个复根，则它的共轭复数也是f（x）的复根。
相似考题
更多“在R[x]上degf（x）=n>0，若c是它的一个复根，则它的共”相关问题
-
第1题：
在一个堆的顺序存储中，若一个元素的下标为i(0≤i≤n-1)，则它的左孩子元素的下标为【 】。
正确答案：2i+1
2i+1 解析：堆的顺序存储是从0开始的，所以其左孩子的元素下标为2i+k，右孩子元素的下标为2i+2。 -
第2题：
将大小为100N的力F沿x、y方向分解，若F在x轴上的投影为50N，而沿x方向的分力的大小为200N，则F在y轴上的投影为（ ）。
A、 0
B、 50N
C、 200N
D、 100N答案：A解析：F为100N，在x轴投影为50N，所以∠FOX=60°。因为F在x轴的分力是200N，所以，根据力的合成与分解原理可知，∠FOY=90°，所以，F在y轴投影为零。 -
第3题：
若一个等腰三角形的两边边长是方程x2-6x+8=0的解，则它的周长是( )。A.6
B.8
C.10
D.8或10答案：C解析：解方程x2-6x+8=0得等腰三角形的两条边为4和2，如果第三条边为2，则与“三角形两边和大于第三边”矛盾，所以第三条边为4。周长=4+4+2=10。 -
第4题：
设r为变量x与y的相关系数，b为y对x的回归系数，则r与b的关系有（ ）。 [2010年真题]
A.若r=l，则b=1 B.若 r=0，则b=0
C.若r= -l，则b= -1 D.若r>0，则b>0
E.若r答案：D,E解析：D项，r>0时两个变量正相关，回归系数b>0； E项，r -
第5题：
设两变量X与Y的观测值为(xi,yi)，i= 1，2，…，n,用r表示相关系数，y = a + bc表示回归方程，以下结论正确的有（ ）。
A.若 r=1，则b=1 B.若 rC.若 r=0，则b= 0 D.若r>0，则b>0
E.若 r = 1，则 a = 0答案：B,C,D解析： -
第6题：
若函数f(x)=(k-1)ax- ax (a＞0且α≠1)在R上既是奇函数，又是减函数，则g(x)=loga (x+k)的图象是( )。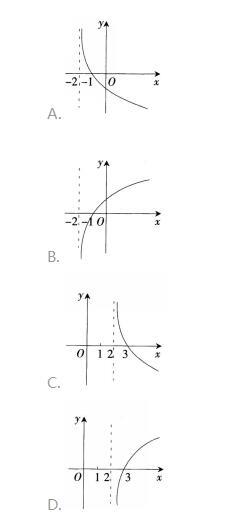
答案：A解析：函数f(x)是奇函数，则有f(0)=(k-1)-1=0，得k=2.f(x)=ax-a-x。又f(x)在R上是减函数，则有0第7题：
用牛顿切线法解方程f（x）=0，选初始值x0满足（），则它的解数列{xn}n=0，1，2，…一定收敛到方程f（x）=0的根。
- A、f（x0）f″（x）>0
- B、f（x0）f′（x）>0
- C、f（x0）f″（x）<0
- D、f（x0）f′（x）<0
正确答案:A第8题：
若f（x）∈F[x]，若c∈F使得f（c）=0，则称c是f（x）在F中的一个根。
正确答案:正确第9题：
若随机变量X服从参数为n和p的二项分布，则它的数学期望为（），方差是（）
正确答案:np；npq第10题：
多选题设r为变量x与y的相关系数，b为y对x的回归系数，则r与b的关系有（ ）。[2010年真题]A若r=l，则b=1
B若r=0，则b=0
C若r=-l，则b=-1
D若r＞0，则b＞0
E若r＜0，划b＜0
正确答案： B,E解析：
D项，r＞0时两个变量正相关，回归系数b＞0；E项，r＜0时两个变量负相关，回归系数b＜0。第11题：
单选题下列说法中正确的是（ ）。[2014年真题]A若f′（x0）=0，则f（x0）必须是f（x）的极值
B若f（x0）是f（x）的极值，则f（x）在点x0处可导，且f′（x0）=0
C若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的必要条件
D若f（x0）在点x0处可导，则f′（x0）=0是f（x）在x0取得极值的充分条件
正确答案： B解析：
当f（x0）在点x0处可导时，若f（x）在x0处取得极值，则可知f′（x0）=0；若f′（x0）＝0，f（x）在点x0未必取得极值，例如f（x）＝x3在点x＝0处有f′（0）＝0，但x3在实数域内不存在极值点。第12题：
判断题在R[x]上degf（x）=n>0，若c是它的一个复根，则它的共轭复数也是f（x）的复根。A对
B错
正确答案： 对解析： 暂无解析第13题：
设f（x）在（-∞，+∞）上是偶函数，若f'（-x0）=-K≠0，则f(x0)等于:
答案：B解析：提示：利用结论“偶函数的导函数为奇函数”计算。
f（-x）=f（x），求导-f'（-x）=f'（x），即f'（-x）=-f'（x）。将x=x0代入，得f'（-x0）=-f'（x0），解出f'（x0）=K。第14题：
下列命题正确的是().
A若|f(x)|在x=a处连续,则f(x)在x=a处连续
B若f(x)在x=a处连续,则|f(x)|在x=a处连续
C若f(x)在x=a处连续,则f(x)在z-a的一个邻域内连续
D若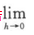
［f(a+h)－f(a-h)］=0,则f(x)在x=a处连续答案：B解析：
第15题：
设两变量X和Y的观测值为(xi,yi), i =1， 2，…n，用r表示相关系数，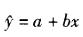
表示回归方程，以下结论正确的有（ ）。
A.若r= 1,则b= 1 B.若rC.若r=0,则b=0 D.若r>0,则b>0
E.若r= 1,则a = 0答案：B,C,D解析：相关系数r值的不同，X和Y的相关性有：①当r=±1时，n个点完全在一条直线上，这时称两个变量完全线性相关；②当r=0时，称两个变量线性不相关，这时散布图上n个点可能毫无规律，不过也可能两个变量间存在某种曲线的趋势，回归方程的斜率为0，即b=0；③当r>0时，称两个变量正相关，这时当x值增加时，y值也有增大的趋势，则其回归方程的斜率为正，即b>0；④当r第16题：
若r是由n对观测值（xi，yi)计算得到的x，y的相关系数，y = a + bx表示相 应的回归方程，则下列说法中，正确的有（ ）。
A.若 r= 1，则 b= 1
B.若 r=﹣1，则 b＜0
C.若r≠0，则/b≠0
D. r与b同号
E. r与a异号答案：B,C,D解析：第17题：
设r是变量X与Y的相关系数，则有（）。
A. 0≤r≤1
B. r 愈大，X与Y间线性关系愈强
C.若r=0，则X与Y间无曲线关系
D. r是无量纲的量
E.若 r =1，则X与Y间无线性关系答案：B,D解析：。r的取值范围为﹣1≤r≤1，而非0≤r≤1，选项A错误。若r=0，则X与Y间无线性相关关系，但可能存在曲线关系，选项C错误。若 r =1，则X与Y间线性关系最强，选项E错误。第18题：
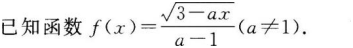
(1)若a>0，则?(x)的定义域是__________；
(2)若?(x)在区间(0，1]上是减函数，则实数a的取值范围是__________．答案：解析：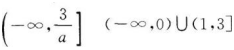
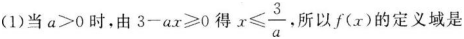
第19题：
设一个关系为R，X和Y是它的两个属性集。若对于X上的每个值都有Y上的一个惟一值与之对应，则称X和Y（）。
- A、属于第一范式
- B、属于第二范式
- C、具有函数依赖关系
- D、具有非函数依赖关系
正确答案:C第20题：
设f（x），g（x）∈F[x]，若f（x）=0则有什么成立？（）
- A、deg（f（x）g（x））
- B、deg（f（x）g（x））＞max{degf（x），degg（x）}
- C、deg（f（x）+g（x））＞max{degf（x），degg（x）}
- D、deg（f（x）+g（x））=max{degf（x），degg（x）}
正确答案:D第21题：
单选题设f（x）g（x）在x0处可导，且f（x0）＝g（x0）＝0，f′（x0）g′（x0）＞0，f″（x0）、g″（x0）存在，则（ ）Ax0不是f（x）g（x）的驻点
Bx0是f（x）g（x）的驻点，但不是它的极值点
Cx0是f（x）g（x）的驻点，且是它的极小值点
Dx0是f（x）g（x）的驻点，且是它的极大值点
正确答案： B解析：
构造函数φ（x）＝f（x）·g（x），则φ′（x）＝f′（x）·g（x）＋f（x）g′（x），φ″（x）＝f″（x）g（x）＋2f′（x）g′（x）＋f（x）g″（x）。
又f（x0）＝g（x0）＝0，故φ′（x0）＝0，x0是φ（x）的驻点。
又因φ″（x0）＝2f′（x0）g′（x0）＞0，故φ（x）在x0取到极小值。第22题：
单选题设一个关系为R，X和Y是它的两个属性集。若对于X上的每个值都有Y上的一个惟一值与之对应，则称X和Y（）。A属于第一范式
B属于第二范式
C具有函数依赖关系
D具有非函数依赖关系
正确答案： B解析： 暂无解析第23题：
单选题设f（x），g（x）∈F[x]，若f（x）=0则有什么成立？（）Adeg（f（x）g（x））
Bdeg（f（x）g（x））＞max{degf（x），degg（x）}
Cdeg（f（x）+g（x））＞max{degf（x），degg（x）}
Ddeg（f（x）+g（x））=max{degf（x），degg（x）}
正确答案： C解析： 暂无解析