函数z=1/（xy）的定义域是不含两坐标轴的二维平面。
题目
函数z=1/（xy）的定义域是不含两坐标轴的二维平面。
相似考题
更多“函数z=1/（xy）的定义域是不含两坐标轴的二维平面。”相关问题
-
第1题：
使用下列二维图形变换矩阵A=a*T，,其中，a是行向量(xy1)，是齐次坐标形式的二维点。给定的变换矩阵T如下所示，则将产生的变换结果为()
A.图形放大2倍
B.图形放大2倍，同时沿X、Y坐标轴方向各移动一个单位
C.沿X坐标轴方向各移动2个单位
D.沿X坐标轴放大2倍，同时沿X、Y坐标轴方向各移动一个单位
正确答案：D
-
第2题：
下列函数定义中，会出现编译错误的是
A．max(int x,int y,int*z) {*z=x＞y?xy;}
B．int max(int x,y) {int z； z=x＞y?xy； return z； }
C．max(int x,int y) {int z； z=x＞y?xy;return(z)； }
D．int max(int x,int y) { return(x＞y?xy)；}
正确答案：B
解析：本题考核的知识点是函数的定义方法。选项B中在说明形参时，省略了第二个参数的类型，故选项B编译不能通过。 -
第3题：
设函数，(u)可导，z=f(sin y-sin x)+xy，则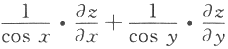
=__________.答案：解析：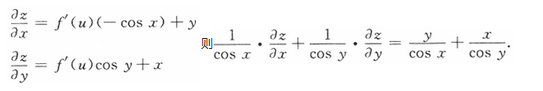
-
第4题：
函数y=的定义域是（ ）A.{x｜ z∈R且x≠}
B.{x｜x≥｝
C.{x｜x≥2}
D.{x｜x≥2或x≤1｝答案：D解析： -
第5题：
最大卸载高度是指（）。
- A、在Z坐标轴方向上，切削刃所能达到的最深点到GRP平面之间的距离
- B、在Z坐标轴方向上，切削刃所能达到的最高点到GRP平面之间的距离
- C、在Z坐标轴方向上，铲斗铰轴处于最高位置时，铲斗可达到的最低点到GRP平面之间的距离
- D、在Z坐标轴方向上，铲斗铰轴处于最高位置时，铲斗可达到的最高点到GRP平面之间的距离
正确答案:C -
第6题：
两函数复合时，中间变量的值域要包含在外层函数的定义域中。
正确答案:正确 -
第7题：
若二元函数z=arctg（xy），则z（x，y）关于x的偏导数在（1，1）点的值是（）。
- A、1/2
- B、1
- C、2
- D、0
正确答案:A -
第8题：
单选题若二元函数z=arctg（xy），则z（x，y）关于x的偏导数在（1，1）点的值是（）。A1/2
B1
C2
D0
正确答案： B解析： 暂无解析 -
第9题：
判断题将平行于XY平面的二维图形沿Z轴方向拉伸生成三维形体的方法叫二维半绘图，二维半绘图生成的是线框模型A对
B错
正确答案： 对解析： 暂无解析 -
第10题：
判断题函数z=1/（xy）的定义域是不含两坐标轴的二维平面。A对
B错
正确答案： 错解析： 暂无解析 -
第11题：
问答题求函数z＝x2－xy＋y2在区域D：|x|＋|y|≤1上的最大、最小值。正确答案：
分别求出z对x、y的偏导,得zx′=2x-y,zy′=2y-x,并令其为0,解得驻点为(0,0)。可知,该驻点在区域D内,且z(0,0)=0。
闭区域D:,x,+,y,≤1的边界由四线段构成:
l1:x+y=1;l2:x-y=1(0≤x≤1)
l 3:x+y=-1;l4:y-x=1(-1≤x≤0)
直线l1上,z=3x2-3x+1,则令zx′=6x-3=0,x=1/2,z(1/2)=1/4,z(0)=1,z(1)=1。
直线l2上,z=x2-x+1,则令zx′=2x-1=0,得x=1/2,z(1/2)=3/4,z(0)=1,z(1)=1。
直线l3上,z=3x2+3x+1,则令zx′=6x+3=0,得x=-1/2,z(-1/2)=1/4,z(-1)=1,z(0)=1。
直线l4上,z=x2+x+1,则令zx′=2x+1=0,得x=-1/2,z(-1/2)=3/4,z(-1)=1,z(0)=1。
比较以上所有函数值,可知函数z在D上的最大值为1,最小值为0。解析： 暂无解析 -
第12题：
单选题函数z=sin（xy）cos（x+y）的定义域是（）。A第一象限
B第一、三象限
CXOY坐标面
D第二、四象限
正确答案： B解析： 暂无解析 -
第13题：
下列关于函数依赖的规则中，正确的是( )。
A．若X→Y，WY→Z，则XY→Z
B．若X∩Y=，则X→Y
C．若XY→Z 则X→Z，Y→Z
D．若YZ， 则Y→Z
正确答案：A
解析：根据函数依赖的几个概念和Armstrong公理系统的推理规则来逐个判断。Armstrong公理系统包括3条推理规则：①自反律。若YXU，则X→Y为F所逻辑蕴含。②增广律。若X→Y为F所逻辑蕴含，且ZU，则XZ→YZ为F所逻辑蕴含。③传递律。若X→Y及Y→Z为F所逻辑蕴含，则X→Z为F所逻辑蕴含。根据以上3条推理规则可以得到以下3条有用的规则：①合并规则。由X→Y，X→Z，有X→YZ。②伪传递规则。由X→Y，WY→Z，有XW→Z。③分解规则。由X→Y及ZY，有X→Z。根据伪传递规则，选项A)是正确的。选项C)是错误的，因为在函数依赖关系中，决定因素的某个真子集不一定能确定一个函数依赖关系。选项B)和D)更是错误。 -
第14题：
设函数z=f(xy，yg(x))，其中函数f具有二阶连续偏导数，函数g(x)可导且在x=1处取得极值g(1)=1.求
答案：解析：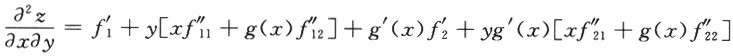
所以，令x=y=1，且注意到g(1)=1，g'(1)=0，得
-
第15题：
假设一个消费者的效用函数为u= xy+y，其中z和y分别表示两种商品。 (1)请问此效用函数是拟凹的吗？ (2)计算均衡需求函数和马歇尔需求函数。 (3)计算间接效用函数和支出函数。答案：解析：(1)该效用函数是拟凹函数。分析如下： 由消费者的效用函数可得商品z和y的边际效用分别为： MU=y，MUy=x+1 因此，边际替代率为： MRS=MUx/MUy=y/x+1 可以看出，边际替代率MRS随着x的增加而减少，因此该函数是拟凹函数。 (2)假设消费者的收入为I，则消费者的效用最大化问题为： max u=xy+y s.t. P1x+P2Y=I 其中，Pl和P2分别为x和y的价格。构造拉格朗日辅助函数L=ry+y-λ(P1x+P2Y-I)，效 用最大化的一阶条件为：
解得：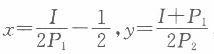
此即为x、y的马歇尔需求函数。 (3)间接效用函数和支出函数： 将最优解代人效用函数可得间接效用函数为：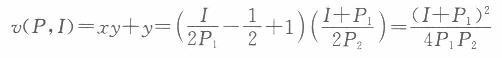
即间接效用函数为
支出函数与间接效用函数互为反函数，因此支出函数为：
-
第16题：
设函数z=xy，则全微分dz_______.答案：解析：
-
第17题：
将平行于XY平面的二维图形沿Z轴方向拉伸生成三维形体的方法叫二维半绘图，二维半绘图生成的是线框模型
正确答案:错误 -
第18题：
函数z=sin（xy）cos（x+y）的定义域是（）。
- A、第一象限
- B、第一、三象限
- C、XOY坐标面
- D、第二、四象限
正确答案:C -
第19题：
若z=xy+sinxy则函数z（x，y）在（0，1）点关于x的偏导数的值是（）。
- A、0
- B、2
- C、1
- D、-1/2
正确答案:B -
第20题：
填空题曲面z－ez＋2xy＝3在点（1，2，0）处的切平面方程为____。正确答案： 4(x-1)+2(y-2)=0解析：
构造函数F（x，y，z）＝z－ez＋2xy－3，则Fx′＝2y，Fy′＝2x，Fz′＝1－ez。故将点（1，2，0）代入上式，即可得此点处切平面的法线向量为n＝（4，2，0），则切平面方程为4（x－1）＋2（y－2）＝0。 -
第21题：
单选题设z＝z（x，y）是由方程xz－xy＋ln（xyz）＝0所确定的可微函数，则∂z/∂y等于（ ）。[2013年真题]A－xz/（xz＋1）
B－x＋1/2
Cz（－xz＋y）/[x（xz＋1）]
Dz（xy－1）/[y（xz＋1）]
正确答案： B解析：
将xz－xy＋ln（xyz）＝0两边对y求偏导，得xzy′－x＋x（z＋y·zy′）/（xyz）＝0，整理得zy′＝z（xy－1）/[y（xz＋1）]。 -
第22题：
单选题设三元函数xy－zlny＋exz＝1，根据隐函数存在定理，存在点（0，1，1）的一个邻域，在此邻域内该方程（ ）。A只能确定一个具有连续偏导数的隐函数z＝z（x，y）
B可确定两个具有连续偏导数的隐函数y＝y（x，z）和z＝z（x，y）
C可确定两个具有连续偏导数的隐函数x＝x（y，z）和z＝z（x，y）
D可确定两个具有连续偏导数的隐函数x＝x（y，z）和y＝y（x，z）
正确答案： C解析：
构造函数F（x，y，z）＝xy－zlny＋exz－1，则Fx′＝y＋zexz，Fy′＝x－（z/y），Fz′＝－lny＋xexz。Fx′（0，1，1）＝2≠0，Fy′（0，1，1）＝－1≠0，Fz′（0，1，1）＝0。
故根据隐函数的存在定理可知，方程xy－zlny＋exz＝1能确定x是y、z的具有连续偏导数的函数x＝x（y，z）；y是x、z的具有连续偏导数的函数y＝y（x，z）。因为Fz′（0，1，1）＝0不能满足定理成立的条件，故不能确定z是x、y的具有连续偏导数的隐函数z＝z（x，y）。 -
第23题：
单选题若z=xy+sinxy则函数z（x，y）在（0，1）点关于x的偏导数的值是（）。A0
B2
C1
D-1/2
正确答案： B解析： 暂无解析