若函数φ（z）在复平面内任意一点的导数都存在，则称这个函数在复平面上什么？（）A、解析B、可导C、可分D、可积

题目

若函数φ（z）在复平面内任意一点的导数都存在，则称这个函数在复平面上什么？（）

  • A、解析
  • B、可导
  • C、可分
  • D、可积
相似考题

1.下列关于部分函数依赖的叙述中，哪一条是正确的？A．若X→Y，且存在属性集Z，Z∩Y≠?，X→Z，则称Y对X部分函数依赖B．若X→Y，且存在属性集Z，Z∩Y=?，X→Z，则称Y对X部分函数依赖C．若X→Y，且存在X的真子集X'Z，X'→Z，则称Y对X部分函数依赖D．若X→Y，且对于X的任何真子集X'，都有X' ?Y，则称Y对X部分函数依赖

2.若函数 f(z) 在点 z0不解析，则称 z0为函数 f(z) 的( )点.

3.如果系统的开环传递函数在复平面s的右半面既没有极点,也没有零点,则称该传递函数为()。A.最小相位传递函数B.积分环节传递函数C.惯性环节传递函数D.微分环节传递函数

4.（ 52 ）下列关于部分函数依赖的叙述中，哪一条是正确的？A ）若 X → Y ，且存在属性集 Z ， Z ∩ Y ≠? ， X → Z ，则称 Y 对 X 部分函数依赖B ）若 X → Y ，且存在属性集 Z ， Z ∩ Y= ? ， X → Z ，则称 Y 对 X 部分函数依赖C ）若 X → Y ，且存在 X 的真子集 X ′ ， X ′→ Y ，则称 Y 对 X 部分函数依赖D ）若 X → Y ，且对于 X 的任何真子集 X ′ ，都有 X ′→ Y ，则称 Y 对 X 部分函数依赖

更多“若函数φ（z）在复平面内任意一点的导数都存在，则称这个函数在复平”相关问题

  • 第1题：

    如果函数在具有任意阶导数,则存在,使得在可以展开成泰勒级数.()

    此题为判断题(对，错)。


    正确答案：错误

  • 第2题：

    在复变函数中，负数也有对数。这一点和实变函数中不同，而且正实数的对数在复变函数中也是无穷多值的。()


    正确答案:对

  • 第3题：

    设有三元方程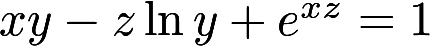 ，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程

    A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
    B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
    C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
    D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)

    答案：D
    解析：

  • 第4题：

    在一个关系R中，若存在X→（Y，Z），则也隐含存在（），称此为函数依赖的（）规则。


    正确答案:X→Y和X→Z；分解性

  • 第5题：

    在一个关系R中，若存在X→（Y，Z），则也隐含存在X→Y和X→Z，称此为函数依赖的（）规则。

    • A、传递性
    • B、分解性
    • C、合并性
    • D、增广性

    正确答案:B

  • 第6题：

    多元函数所有偏导数都存在，则这个函数必可微。


    正确答案:错误

  • 第7题：

    函数在一点处的左右极限都存在，则函数在这一点的极限存在。


    正确答案:错误

  • 第8题：

    如果系统的开环传递函数在复平面s的右半面既没有极点，也没有零点，则称该传递函数为（）。

    • A、最小相位传递函数
    • B、积分环节传递函数
    • C、惯性环节传递函数
    • D、微分环节传递函数

    正确答案:A

  • 第9题：

    若z=xy+sinxy则函数z（x，y）在（0，1）点关于x的偏导数的值是（）。

    • A、0
    • B、2
    • C、1
    • D、-1/2

    正确答案:B

  • 第10题：

    判断题
    若z=f(x,y)在（x0,y0）处的两个一阶偏导数存在，则函数z=f(x,y)在(x0,y0)处可微
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第11题：

    单选题
    设三元函数xy－zlny＋exz＝1，根据隐函数存在定理，存在点（0，1，1）的一个邻域，在此邻域内该方程（　　）。
    A

    只能确定一个具有连续偏导数的隐函数z＝z（x，y）

    B

    可确定两个具有连续偏导数的隐函数y＝y（x，z）和z＝z（x，y）

    C

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和z＝z（x，y）

    D

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和y＝y（x，z）


    正确答案： C
    解析：
    构造函数F（x，y，z）＝xy－zlny＋exz－1，则Fx′＝y＋zexz，Fy′＝x－（z/y），Fz′＝－lny＋xexz。Fx′（0，1，1）＝2≠0，Fy′（0，1，1）＝－1≠0，Fz′（0，1，1）＝0。
    故根据隐函数的存在定理可知，方程xy－zlny＋exz＝1能确定x是y、z的具有连续偏导数的函数x＝x（y，z）；y是x、z的具有连续偏导数的函数y＝y（x，z）。因为Fz′（0，1，1）＝0不能满足定理成立的条件，故不能确定z是x、y的具有连续偏导数的隐函数z＝z（x，y）。

  • 第12题：

    判断题
    函数在一点处的左右极限都存在，则函数在这一点的极限存在。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    下列关于部分函数依赖的叙述中，哪一条是正确的?

    A．若X→Y，且存在属性集Z，Z∩Y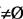，Y→Z，则称Y对X部分函数依赖

    B．若X→Y，且存在属性集Z，Z∩Y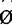，Y→Z，则称Y对X部分函数依赖

    C．若X→Y，且存在X的真子集X'，X'→Y，则称Y对X部分函数依赖

    D．若X→Y，且对于X的任何真子集X'，都有X'→Y\，则称Y对X部分函数依赖


    正确答案：C
    解析：本题是对函数依赖定义和公理的考查。选项A、B显然是不正确的；按照函数部分依赖的定义选项C(若X→Y，且存在X的真子集X'，X'→Y，则称Y对X部分函数依赖)是正确的。而D(若X→Y，且对于X的任何真子集X'，都有X'≠＞Y，则称Y对X部分函数依赖)是错误的，因为若X→Y，且对于X的任何真子集X'，都有X'≠＞Y，则称Y对X是完全函数依赖。所以本题正确答案为选项C。

  • 第14题：

    下列关于部分函数依赖的叙述中，______是正确的。

    A．若X→Y，且存在属性集Z，Z∩Y≠Φ，X→Z，则称Y对X的部分函数依赖

    B．若X→Y，且存在属性集Z，Z∩y＝Φ，X→Z，则称Y对X的部分函数依赖

    C．若X→Y，且存在X的真子集X'，X'→Y，则称Y对X的部分函数依赖

    D．若X→Y，且对于X的任何真子集X'，都有X'→Y，则称Y对X的部分函数依赖


    正确答案：C
    解析：在关系模式RU，F＞中，如果X→Y，且存在X的一个真子集X'，有X'→Y，则称Y对X的依赖为部分函数依赖。这是部分函数依赖的定义。

  • 第15题：

    若z=f(x,y)在（x0,y0）处的两个一阶偏导数存在，则函数z=f(x,y)在(x0,y0)处可微


    正确答案:错误

  • 第16题：

    在一个关系R中，若存在X→Y和X→Z，则存在X→（Y，Z），称此为函数依赖的（）规则。

    • A、传递性
    • B、分解性
    • C、合并性
    • D、增广性

    正确答案:C

  • 第17题：

    在一个关系R中，若存在X→（Y，Z），则存在X→Y，X→Z，称此为函数依赖的（）规则。

    • A、传递性
    • B、分解性
    • C、合并性
    • D、增广性

    正确答案:B

  • 第18题：

    若二元函数z=arctg（xy），则z（x，y）关于x的偏导数在（1，1）点的值是（）。

    • A、1/2
    • B、1
    • C、2
    • D、0

    正确答案:A

  • 第19题：

    下列关于势函数和流函数的说法错误的是（）

    • A、在平面不可压流场中，势函数和流函数同时存在。
    • B、势函数在某个方向的偏导数等于速度在那个方向的分量。
    • C、流函数线的切线方向与速度矢量方向重合。
    • D、过同一点的等速度势函数线与等流函数线正交

    正确答案:A,B

  • 第20题：

    在一个关系R中，若存在X→（Y，Z），则也隐含存在（X→Y）和（X→Z），称此为函数依赖的（）规则。


    正确答案:分解性

  • 第21题：

    判断题
    多元函数所有偏导数都存在，则这个函数必可微。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第22题：

    单选题
    若函数φ（z）在复平面内任意一点的导数都存在，则称这个函数在复平面上什么？（）
    A

    解析

    B

    可导

    C

    可分

    D

    可积


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    若z=xy+sinxy则函数z（x，y）在（0，1）点关于x的偏导数的值是（）。
    A

    0

    B

    2

    C

    1

    D

    -1/2


    正确答案： B
    解析： 暂无解析

相关内容