问答题已知消费函数为C=100+0.6Y,投资为自主投资,I=60,求: (1)均衡的国民收入(Y)为多少? (2)均衡的储蓄量(S)为多少? (3)如果充分就业的国民收入水平为Yf=1000,那么,为使该经济达到充分就业的均衡状态,投资量应如何变化? (4)本题中投资乘数(k)为多少?
题目
相似考题
更多“问答题已知消费函数为C=100+0.6Y,投资为自主投资,I=60,求: (1)均衡的国民收入(Y)为多少? (2)均衡的储蓄量(S)为多少? (3)如果充分就业的国民收入水平为Yf=1000,那么,为使该经济达到充分就业的均衡状态,投资量应如何变化? (4)本题中投资乘数(k)为多少?”相关问题
-
第1题:
已知某国的投资函数为I=300-100r,储蓄函数为S=-200+0.2Y,货币需求为L=0.4Y-50r,该国的货币供给量M=250,价格总水平P=1。
(1)写出IS和LM曲线方程;
(2)计算均衡的国民收入和利息率;
(3)在其他条件不变情况下,政府购买增加100,均衡国民收入增加多少?
正确答案:(1)IS曲线:300-100r=-200+0.2Y
LM曲线:0.4Y-50r=250
(2)求解:300-100r=-200+0.2Y
0.4Y-50r=250
得到:Y=1000
r=3
(3)C=100,则IS-LM方程为
100+300-100r=-200+0.2Y
0.4Y-50r=250
解得:Y=1100,因此,国民收入增加100。 -
第2题:
假设某经济社会储蓄函数为s=-1000+0.25y,投资从300增加到500时,均衡收入增加多少?若本期消费是上期收入的函数,即C=a+bYt-1,试求投资从300增至500过程中的第1、2、3、4期收入各为多少?
参考答案:当s=-1000+0.25y,,I=300时,Y=(1000+300)/0.25=5200当投资增至500时,Y=(1000+500)/0.25=6000若消费是上一期收入的函数,则投资从300增至500过程中,第1、2、3、4期收入分别是:Y1=0.75×5200+1000+500=5400;Y2=0.75×5400+1000+500=5550;Y3=0.75×5550+1000+500=5662.5;Y4=0.75×5662.5+1000+500=5746.875(提示:上述各期收入也可以通过差分方程的通解中直接解出)
-
第3题:
已知一个宏观经济中的消费函数为C =100 +0. 8Yd(Yd为可支配收入,单位为亿元),自发(主)投资1= 50,政府财政政策包括政府支出G=200,定量(或自主)税收To =60,比例税率t=0. 25。求: (1)宏观经济均衡时的国民收入y是多少? (2)(支出)乘数K是多少? (3)政府的财政盈余是多少?答案:解析:
-
第4题:
假设某经济的消费函数为c =1000 +0,75yd,,投资为i=800,政府购买为g=7_0,净税收为t= 600。试求:(l)均衡国民收入和可支配收入;(2)消费支出:(3)私人储蓄和政府储蓄;(4)投资乘数。答案:解析:(l)y=c+i+g=0.75y+2100, y*= 8400,yd= 8400 - 600= 7800。 (2)c =1000 +0.75 x7800 =6850。 (3)私人储蓄=y-t-c=950, 政府储蓄=t-g= -150。 (4)边际消费倾向为0.75,投资乘数为4。 -
第5题:
假设某经济的消费函数为c=100+0.8yd,投资i=50,政府购买性支出g=200,政府转移支付tr=62.5,税收t=250(单位均为10亿美元)。 (1)求均衡收入; (2)求投资乘数、政府支出乘数、税收乘数、转移支付乘数、平衡预算乘数; (3)假定该社会达到充分就业所需要的国民收入为1200,试问: ①增加政府购买; ②减少税收; ③以同一数额增加政府购买和税收(即平衡预算)实现充分就业,各需多少数额?
正确答案: (1)y=c+i+g=100+0.8yd+50+200,yd=y-t +tr=y-250+62.5,均衡收入y=1000;
(2)投资乘数=政府支出乘数=1/(1-0.9)=5;税收乘数=-0.9/(1-0.9)= -4;政府转移支付乘数=4;平衡预算乘数=1;
(3)国民收入增量为200,1)增加政府购买为200/5=40;2)减少税收为200/4=50,3)各200。 -
第6题:
假定某经济的消费函数为C=100+0.8DI,DI为可支配收入,投资I=50,政府购买G=200,政府转移支付Tr=62.5,税收t=250.试求:均衡的国民收入?投资乘数、政府购买乘数、转移支付乘数、平均预算乘数各为多少?
正确答案:(1)可支配收入DI=NI-t+Tr=NI-250+62.5=NI-187.5
由收入恒等式NI=C+I+G=100+0.8(NI-187.5)+50+200
解得均衡国民收入=1000(亿元)
(2)根据消费函数可知边际消费倾向c=0.8,则:
投资乘数=1/1-c=5
政府购买乘数=1/1-c=5
税收乘数=-c/1-c=-4
转移支付乘数=c/1-c=4
平衡预算乘数=1-c/1-c=1 -
第7题:
计算题:假设经济体系中消费函数为C=600+0.8Y,投资函数为I=400—50r,政府购买G=200,货币需求函数MD=250+0.5Y-125r,货币供给MS=l250(单位均为亿美元)。试求:(1)均衡收入和利率是多少?(2)若充分就业收入为Y*=5000(亿美元),用增加政府购买实现充分就业,要增加多少购买?(3)若用增加货币供给实现充分就业,要增加多少货币供应量?
正确答案:(1)由Y=C+I+G得IS曲线方程:
Y=600+0.8Y+400-50r+200
即0.2Y=1200-50r
Y=6000-250r
由MS=MD得LM曲线方程为:
250+0.5Y-125r=l250
即Y=2000+250r
联立LS-LM方程解得:6000-250r=2000+250r
均衡利率为:r=8
均衡收入为:Y=4000(亿美元)
(2)若充分就业收入为Y*=5000(亿美元)
由LM曲线方程得均衡利率r*=(5000-2000)/250=12
由IS曲线方程得:Y=C+I+G=600+0.8Y+400-50r+G
5000=600+4000+400-600+G*
G*=600
⊿G=G*-G=600-200=400(亿美元)
(3)若用增加货币供给实现充分就业,由IS曲线方程得均衡利率,
0.2×5000=1200-50r*
r*=4
由MS=MD=250+0.5Y-125r,得:
MS*=250+0.5×5000-125×4=2250(亿美元)
⊿MS=MS*-MS=2250-1250=1000(亿美元) -
第8题:
问答题假设某经济社会的消费函数为C=1000+0.8Y,投资为500亿美元。 (1)求均衡收入、消费和储蓄; (2)如果当时实际产出为8000亿美元,企业非意愿存货变动多少; (3)若投资增至1000亿美元,求增加的收入; (4)若消费函数变为C=1000+0.9Y,乘数如何变化正确答案: (1)Y=(1000+500)/(1-0.8)=7500,C=1000+0.8×7500=7000,S=Y-C=7500-7000=500
(2)8000-(1000+0.8×8000+500)=100
(3)Y=(1000+1000)/(1-0.8)=10000,比原来的收入增加2500亿美元
(4)乘数K=1/(1-0.8)=5变为K=(1-0.9)=10解析: 暂无解析 -
第9题:
问答题假设某经济的消费函数为c=100+0.8yd,投资i=50,政府购买性支出g=200,政府转移支付tr=62.5,税收t=250(单位均为10亿美元)。 (1)求均衡收入; (2)求投资乘数、政府支出乘数、税收乘数、转移支付乘数、平衡预算乘数; (3)假定该社会达到充分就业所需要的国民收入为1200,试问: ①增加政府购买; ②减少税收; ③以同一数额增加政府购买和税收(即平衡预算)实现充分就业,各需多少数额?正确答案: (1)y=c+i+g=100+0.8yd+50+200,yd=y-t +tr=y-250+62.5,均衡收入y=1000;
(2)投资乘数=政府支出乘数=1/(1-0.9)=5;税收乘数=-0.9/(1-0.9)= -4;政府转移支付乘数=4;平衡预算乘数=1;
(3)国民收入增量为200,1)增加政府购买为200/5=40;2)减少税收为200/4=50,3)各200。解析: 暂无解析 -
第10题:
问答题假设某经济社会储蓄函数为s=-1000+0.25y,投资从300增加到500时,均衡收入增加多少?若本期消费是上期收入的函数,即C=a+bYt-1,试求投资从300增至500过程中的第1、2、3、4期收入各为多少?正确答案: 当s=-1000+0.25y,,I=300时,Y=(1000+300)/0.25=5200当投资增至500时,Y=(1000+500)/0.25=6000若消费是上一期收入的函数,则投资从300增至500过程中,第1、2、3、4期收入分别是:Y1=0.75×5200+1000+500=5400;Y2=0.75×5400+1000+500=5550;Y3=0.75×5550+1000+500=5662.5;Y4=0.75×5662.5+1000+500=5746.875(提示:上述各期收入也可以通过差分方程的通解中直接解出)解析: 暂无解析 -
第11题:
问答题假定某国消费函数为C=100+0.8Yd,投资I为50,政府购买G为200,转移支付TR为62.5,单位均为10亿美元,税率t为0.25。 (1)求均衡收入。 (2)求预算盈余BS。 (3)若充分就业收入Y*=1200,当投资为50时,充分就业预算盈余BS*为多少?与实际预算盈余BS相比,说明什么? (4)若投资为50,政府购买增至250,而充分就业收入仍为1200,试问充分就业预算盈余BS*为多少?与实际预算盈余BS相比,说明什么?正确答案:
(1)由国民收入核算恒等式Y=C+I+G,可得:
Y=100+0.8[(1-0.25)Y+62.5]+50+200
解得:均衡收入Y=1000。
(2)税收收入为250(=1000×0.25),政府支出为262.5(=200+62.5),因此,预算盈余为:BS=250-262.5=-12.5。
(3)充分就业时的税收收入为300(=1200×0.25),此时,政府支出仍为262.5(=200+62.5),因此,预算盈余为:BS=300-262.5=37.5。
(4)充分就业时的税收收入为300(=1200×0.25),此时,政府支出变为312.5(=250+62.5),因此,预算盈余为:BS=300-312.5=-12.5。这与实际预算盈余相等。这说明通过增加政府购买实现充分就业时,预算盈余不受影响。解析: 暂无解析 -
第12题:
问答题假设某经济社会的消费函数为C=100+0.8y,投资为50(单位:l0亿美元)。 (1)求均衡收入、消费和储蓄。 (2)如果当时实际产出(即收入)为800,试求企业非意愿存货积累为多少? (3)若投资增至100,试求增加的收入。 (4)若消费函数变为c=100+0.9y,投资仍为50,收入和储蓄各为多少?投资增至100时收入增加多少? (5)消费函数变动后,乘数有何变化?正确答案: (1)y=c+I=100+0.8y+500.2y=150y=750,c=100+0.8×750=700,s=750-700=50
(2)IU=800-750=50
(3)y=c+I=100+0.8y+1000.2y=200y’=1000,Δy=1000-750=250
(4)y=c+I=100+0.9y+500.1y=150y=1500,s=-100+0.1×1500=50,y=c+I=100+0.9y+1000.1y=200y’=2000,Δy=2000-1500=500
(5)乘数变大,由5变为10。解析: 暂无解析 -
第13题:
假设某经济社会的消费函数为C=100+0.8y,投资为50(单位:l0亿美元)。
(1)求均衡收入、消费和储蓄。
(2)如果当时实际产出(即收入)为800,试求企业非意愿存货积累为多少?
(3)若投资增至100,试求增加的收入。
(4)若消费函数变为c=100+0.9y,投资仍为50,收入和储蓄各为多少?投资增至100时收入增加多少?
(5)消费函数变动后,乘数有何变化?
参考答案:(1)y=c+I=100+0.8y+500.2y=150y=750,c=100+0.8×750=700,s=750-700=50
(2)IU=800-750=50
(3)y=c+I=100+0.8y+1000.2y=200y’=1000,Δy=1000-750=250
(4)y=c+I=100+0.9y+500.1y=150y=1500,s=-100+0.1×1500=50,y=c+I=100+0.9y+1000.1y=200y’=2000,Δy=2000-1500=500
(5)乘数变大,由5变为10。
-
第14题:
(1)若投资函数为i= 100(亿美元)一5r,找出利率r为4%、5%、6%、7%时的投资量. (2)若储蓄为S= -40(亿美元)+0.25y,找出与上述投资相均衡的收入水平: (3)求IS曲线并作出图形。答案:解析:(1)由=100(亿美元)- Sr可知,当r=4%时,i=100 -5 x4 =80(亿美元);当r=5%时,=100-5 x5 =75(亿美元);当r=60/0时,1=100 -5 x6 =70(亿美元);当r=7%时,i=100 -5 x7 =65(亿美元)。 (2)由i=s,即100 - Sr= - 40 +0. 25y,解得y=560 - 20r。当r=4时,y=480(亿美元);当r=5时,y =460(亿美元);当r=6时,y=440(亿美元);当r=7时,y=420(亿美元)。 (3) IS曲线如图14-8所示。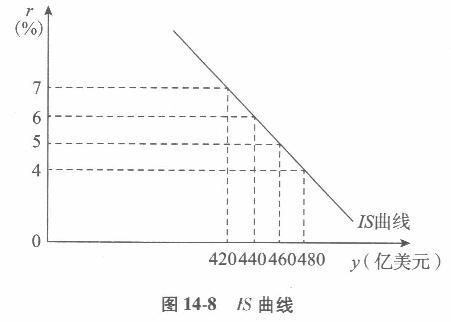
-
第15题:
假设在一个只有家庭和企业的两部门经济中,l7为收入,消费函数为C= 1000+0.8Y,投资I=1000。(单位:10亿元) (1)求均衡收入及相应的消费和储蓄额。 (2)当实际收入为12000时,求社会的非自愿存货;并回答收入将如何变化,并解释收入变化的原因。 (3)如果把投资增加400,相应增加的均衡收入是多少? (4)投资乘数是多少?答案:解析:(1)由Y=C+I可得Y=1000 +0.8Y+1000, 得Y*= 10000。 此时C= 1000 +0.8×10000= 9000,S=l,-C=1000. (2)当y=12000时,C=1000+0.8×12000= 10600,C+1= 11600. 故社会非自愿存货为12000 -11600= 400。 总收入会减少。因为总产出大于总需求,社会非自愿存货使得厂商减少生产。 (3)当1=1400时,由Y=C+I可得l,=IOOO +0. 8Y +1400, 得Y*= 12000, △Y*=2000. (4)投资乘数K=1/(1-MPC)=5 -
第16题:
假设某社会经济的储蓄函数为s=-1600 +0. 25y,投资从i=400增加到i=600时,均衡国民收入增加多少?答案:解析:i=400时,均衡国民收入为8000; i=600时,均衡国民收入为8800; 因此增长了800。 -
第17题:
假设某经济社会的消费函数为C=1000+0.8Y,投资为500亿美元。 (1)求均衡收入、消费和储蓄; (2)如果当时实际产出为8000亿美元,企业非意愿存货变动多少; (3)若投资增至1000亿美元,求增加的收入; (4)若消费函数变为C=1000+0.9Y,乘数如何变化
正确答案:(1)Y=(1000+500)/(1-0.8)=7500,C=1000+0.8×7500=7000,S=Y-C=7500-7000=500
(2)8000-(1000+0.8×8000+500)=100
(3)Y=(1000+1000)/(1-0.8)=10000,比原来的收入增加2500亿美元
(4)乘数K=1/(1-0.8)=5变为K=(1-0.9)=10 -
第18题:
某三部门经济的消费函数为C=80+0.8YD,投资函数为I=20-5r,货币需求函数为L=0.4Y-10r,税收T=0.25Y,政府购买支出为G=20名义货币供给量M=90,充分就业的国民收入为285。若价格水平为P=2,则IS-LM模型决定的均衡收入和利率各为多少?
正确答案:IS曲线。根据三部门的均衡:i+g=s+t。所以(20-5r)+20=(Yd-C)+0.25Y,
因此(20-5r)+20=(0.2Yd-80)+0.25Y,而Yd=Y-T=0.75Y,
所以(20-5r)+20=0.4Y-80,即0.4Y=120-5r
LM曲线,根据货币市场均衡条件:l=M/P。所以0.4Y-10r=90/2,即0.4Y=45+10r
IS-LM决定的均衡国民收入与利率分别为:r=5,Y=237.5 -
第19题:
假设某经济社会的消费函数为C=100+0.8Y,投资为50(单位:10亿美元)。 (1)求均衡产出、消费和储蓄。 (2)如果当时实际产出(即GNP或收入)为800,企业非意愿存货积累是多少? (3)若投资增加至100,求增加的收入。 (4)若消费函数变为C=100+0.9Y,投资仍为50,收入和储蓄各为多少?投资增至100时收入增加多少? (5)消费函数变动后,乘数有什么变化?
正确答案:(1)已知C=100+0.8Y,I=50,根据均衡国民收入的决定公式Y=C+I,Y=100+0.8Y+50
所以,均衡产出为Y=(100+50)/(1-0.8)=750
这样,C=100+0.8×750=700;S=Y-C=750-700=50
储蓄也可以从储蓄函数中求:S=-a+(1-b)Y=-100+0.2×750=50
(2)当均衡产出为750时,企业非意愿存货积累为:800-750=50。
(3)若投资增至100,则收入Y’=(100+100)/(1-0.8)=800。比原来的收入750增加50。
(4)若消费函数变为C=100+0.9Y,相应的均衡国民收入Y=(100+50)/(1-0.9)=1500,S=-a+(1-b)Y=-100+(1-0.9)×1500=50。
若投资增至100,则收入Y=(100+100)/(1-0.9)=2000,比原来的收入1500增加500。
(5)消费函数从C =100+0.8Y,变为C=100+0.9Y以后,乘数从5(K=1/(1-0.8)=5)变为10(K=1/(1-0.9)=10)。 -
第20题:
问答题已知消费函数为C=100+0.6Y,投资为自主投资,I=60,求: (1)均衡的国民收入(Y)为多少? (2)均衡的储蓄量(S)为多少? (3)如果充分就业的国民收入水平为Yf=1000,那么,为使该经济达到充分就业的均衡状态,投资量应如何变化? (4)本题中投资乘数(k)为多少?正确答案:
(1)根据产品市场的均衡条件:Y=C+I=100+0.6Y+60。
解得:均衡的国民收入为Y=400。
(2)当S=I时,产品市场处于均衡状态。因此,均衡的储蓄量S=I=60。
(3)充分就业的国民收入水平为Yf=1000,则当经济实现充分就业均衡时,消费为:
C=100+0.6×1000=700
那么储蓄为:
S=Yf-C=1000-700=300
因此,在充分就业均衡状态时,投资量为:I=S=300。
可见,为使该经济达到充分就业的均衡状态,投资量应增加300-60=240。
(4)投资乘数为:k=ΔY/ΔI=(1000-400)/(300-60)=2.5。解析: 暂无解析 -
第21题:
问答题假定某经济的消费函数为C=100+0.8DI,DI为可支配收入,投资I=50,政府购买G=200,政府转移支付Tr=62.5,税收t=250.试求:均衡的国民收入?投资乘数、政府购买乘数、转移支付乘数、平均预算乘数各为多少?正确答案: (1)可支配收入DI=NI-t+Tr=NI-250+62.5=NI-187.5
由收入恒等式NI=C+I+G=100+0.8(NI-187.5)+50+200
解得均衡国民收入=1000(亿元)
(2)根据消费函数可知边际消费倾向c=0.8,则:
投资乘数=1/1-c=5
政府购买乘数=1/1-c=5
税收乘数=-c/1-c=-4
转移支付乘数=c/1-c=4
平衡预算乘数=1-c/1-c=1解析: 暂无解析 -
第22题:
问答题假设某经济社会的消费函数为C=100+0.8Y,投资为50(单位:10亿美元)。 (1)求均衡产出、消费和储蓄。 (2)如果当时实际产出(即GNP或收入)为800,企业非意愿存货积累是多少? (3)若投资增加至100,求增加的收入。 (4)若消费函数变为C=100+0.9Y,投资仍为50,收入和储蓄各为多少?投资增至100时收入增加多少? (5)消费函数变动后,乘数有什么变化?正确答案: (1)已知C=100+0.8Y,I=50,根据均衡国民收入的决定公式Y=C+I,Y=100+0.8Y+50
所以,均衡产出为Y=(100+50)/(1-0.8)=750
这样,C=100+0.8×750=700;S=Y-C=750-700=50
储蓄也可以从储蓄函数中求:S=-a+(1-b)Y=-100+0.2×750=50
(2)当均衡产出为750时,企业非意愿存货积累为:800-750=50。
(3)若投资增至100,则收入Y’=(100+100)/(1-0.8)=800。比原来的收入750增加50。
(4)若消费函数变为C=100+0.9Y,相应的均衡国民收入Y=(100+50)/(1-0.9)=1500,S=-a+(1-b)Y=-100+(1-0.9)×1500=50。
若投资增至100,则收入Y=(100+100)/(1-0.9)=2000,比原来的收入1500增加500。
(5)消费函数从C =100+0.8Y,变为C=100+0.9Y以后,乘数从5(K=1/(1-0.8)=5)变为10(K=1/(1-0.9)=10)。解析: 暂无解析 -
第23题:
问答题设某国经济可以用以下等式描述:C=90+0.9Yd;I=200-1000i;L=Y-1000i;t=1/3;G=710;M/P=2220。求: (1)IS曲线和LM曲线的表达式。 (2)均衡国民收入水平及均衡利率水平各为多少? (3)私人消费及投资各为多少?政府有预算赤字还是盈余?其值为多少?正确答案: (1)三部门经济均衡条件为:I+G=S+T。
t=1/3,根据可支配收入定义,Yd=(1-t)Y=2Y/3,
因此储蓄函数:S=Yd-C=-90+0.1Yd=-90+Y/15。
将相关函数代入均衡条件可得IS曲线方程为:Y=2500-2500i。
货币市场均衡条件是L=M/P,将货币需求函数L=Y-1000i和实际货币供给函数M/P=2220代入均衡条件可得LM曲线方程为:Y=2220+1000i。
(2)联立IS曲线方程和LM曲线方程可得:Y=2300,i=8%。
即均衡国民收入水平及均衡利率水平各为2300和8%。
(3)把均衡收入水平和均衡利率水平代入消费函数和投资函数可得:私人消费C=90+0.9Yd=1470,投资I=200-1000i=120。税收T=tY=2300/3,大于政府购买支出710,因此政府有预算盈余,政府预算盈余BS=T-G=170/3。解析: 暂无解析 -
第24题:
问答题某国的投资函数和消费函数分别为: I=150 C=0.6Y+100 (1)求均衡国民收入。 (2)当消费函数变为C=0.8Y+100时,均衡国民收入如何变化,比较投资乘数的大小。 (3)当投资函数变为I=200时,均衡国民收入如何变化?正确答案: (1)由两部门经济国民收入恒等式可得:
Y=C+I=0.6Y+100+150
解得:Y=625。
投资乘数为:KI=1/(1-MPC)=1/(1-0.6)=2.5
(2)当消费函数变为C=0.8Y+100时,由两部门经济国民收入恒等式可得:
Y=0.8Y+100+150
解得:Y=1250。
此时投资乘数为:KI=1/(1-MPC)=1/(1-0.8)=5
显然,(1)中投资乘数比(2)中投资乘数要小些,这是因为(2)中的边际消费倾向要大些,即消费对收入较敏感,收入的较小变化就能引起消费的较大变化。
(3)当投资函数变为I=200时,则有:
Y=0.6Y+100+200
解得:Y=750。
从而ΔI=200-150=50,ΔY=750-625=125。
均衡国民收入因投资量增加50而增加125。解析: 暂无解析
