单选题根据样本信息推断总体均值的置信区间为90%，意味着有90%的机会是（）A 估计值等于总体均值的真值B 实际总体均值不超过置信区间的最大下限C 标准差不大于总体平均值的10%D 实际总体均值存在于给定的置信区间内

题目
单选题
根据样本信息推断总体均值的置信区间为90%，意味着有90%的机会是（）
A

估计值等于总体均值的真值

B

实际总体均值不超过置信区间的最大下限

C

标准差不大于总体平均值的10%

D

实际总体均值存在于给定的置信区间内

相似考题

1.根据一个具体的样本求出置信水平为95%的总体均值置信区间()。A、以95%的概率包含总体均值B、以5%的概率包含总体均值C、一定包含总体均值D、可能包含总体均值，也可能不包含总体均值

2.根据一个具体样本求出的总体均值的95%的置信区间()。A.以95%的概率包含总体均值B.有5%的可能性包含总体均值C.一定包含总体均值D.要么包含总体均值，要么不包含总体均值

3.使用同一组样本根据正态分布估计总体均值时，如果将置信度由95%调整为90%，则（ ）。A.将增大B.将减小C.样本均值保持不变D.置信区间宽度减小E.置信区间宽度增加

4.下列关于被解释变量的预测置信区间的描述正确的是()。A.预测置信区间的宽度与样本容量的大小无关B.总体均值和个别值的预测置信区间都以总体均值的点预测为中心C.总体均值的预测置信区间比个别值的预测区间窄D.总体均值和个别值的预测置信区间都在样本均值点处最窄

更多“根据样本信息推断总体均值的置信区间为90%，意味着有90%的机会是（）”相关问题

  • 第1题：

    已知总体服从正态分布，且总体标准差σ，从总体中抽取样本容量为n的产品，测得其样本均值为x，在置信水平为1-a=95%下，总体均值的置信区间为( )


    正确答案：A

  • 第2题：

    使用同一组样本根据正态分布估计总体均值时，如果将置信度由95%调整为90%，则样本均值保持不变。

    此题为判断题(对，错)。


    正确答案：√

  • 第3题：

    根据样本信息推断总体均值的置信区间为90%，意味着有90%的机会是：

    A.估计值等于总体均值的真值
    B.实际总体均值不超过置信区间的最大下限
    C.标准差不大于总体平均值的10%
    D.实际总体均值存在于给定的置信区间内

    答案：D
    解析：

  • 第4题：

    有30个调查者分别对同一正态总体进行了随机抽样，样本量都是100，总体方差未知。调查者分别根据各自的样本数据得到总体均值的一个置信度90%的置信区间，这些置信区间中包含总体均值的区间有（）

    • A、30个
    • B、90个
    • C、27个
    • D、3个

    正确答案:C

  • 第5题：

    已知正态总体标准差为10，样本量n=25，置信水平为95%，Z=1.96，样本均值=105.36。则以下正确的有（）

    • A、样本均值的标准差为10
    • B、样本均值的标准差为2
    • C、样本均值的置信区间为（101.44，109.28）
    • D、总体均值的置信区间为（101.44，109.28）

    正确答案:B,D

  • 第6题：

    根据一个具体的样本求出的总体均值90%的置信区间（）


    正确答案:以90%的概率包含总体均值

  • 第7题：

    正态均值的90%的置信区间是从13.8067至18.1933。这个意思是：（）

    • A、均值落在13.8067至18.1933范围内的概率是90%
    • B、总体中所有值的90%落在13.8067至18.1933
    • C、总体中所有样本值的90%落在13.867至13.1933
    • D、置信区间变差均值的概率为90%

    正确答案:C

  • 第8题：

    统计推断的目的是提供的信息（）。

    • A、基于总体信息的样本
    • B、基于样本信息的总体
    • C、基于总体信息的总体
    • D、基于总体均值的样本均值

    正确答案:B

  • 第9题：

    判断题
    使用同一组样本根据正态分布估计总体均值时，如果将置信度由95%调整为90%，则样本均值保持不变。
    A

    对

    B

    错


    正确答案： 对
    解析：

  • 第10题：

    单选题
    有30个调查者分别对同一正态总体进行了随机抽样，样本量都是100，总体方差未知。调查者分别根据各自的样本数据得到总体均值的一个置信度90%的置信区间，这些置信区间中包含总体均值的区间有（）
    A

    30个

    B

    90个

    C

    27个

    D

    3个


    正确答案： B
    解析： 暂无解析

  • 第11题：

    填空题
    根据一个样本均值求出的90%的置信区间表明（）

    正确答案： 总体均值有90%的概率会落入该区间内
    解析： 暂无解析

  • 第12题：

    填空题
    根据一个具体的样本求出的总体均值95%的置信区间（）

    正确答案： 以95%的概率包含总体均值
    解析： 暂无解析

  • 第13题：

    设X～N(μ，0.09)从中随机抽取样本量为4的样本，其样本均值为，则总体均值μ的 0.95的置信区间为( )。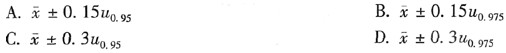


    正确答案：B
    解析：由X～N(μ，0.09)可知该总体标准差已知，用正态分布得μ的1-α的置信区间为。所以μ的0.95的置信区间=。

  • 第14题：

    对样本平均数进行双尾假设检验,在α=0.10水平上拒绝了虚无假设。如果用相同数据计算总体均值1-α=0.90的置信区间,下列描述正确的是()

    A.置信区间不能覆盖总体均值
    B.置信区间覆盖总体均值的概率为10%
    C.置信区间覆盖总体均值的概率为90%
    D.置信区间覆盖总体均值的概率为0.9%

    答案：C
    解析：
    1-α=0.90的置信区间,即估计总体参数落在某一区间的正确率:所以该题为置信区间覆盖总平均值的概率为90%:从题干“对样本平均数进行双尾假设测验，在a=0.10水平上拒绝了虚无假设”，还可以知道置信区间覆盖总体均值的概率超过了90%.

  • 第15题：

    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。


    正确答案:χ±tα/2(20-1)S/√20

  • 第16题：

    设总体X的方差为1，从总体中随机取容量为100的样本，得样本均值等于5，则总体均值的置信水平为99%的置信区间（）。（Z0.005=2.58）


    正确答案:[4.742，5.258]或5±0.258

  • 第17题：

    根据一个样本均值求出的90%的置信区间表明（）


    正确答案:总体均值有90%的概率会落入该区间内

  • 第18题：

    根据一个具体的样本求出的总体均值95%的置信区间（）


    正确答案:以95%的概率包含总体均值

  • 第19题：

    总体均值的置信水平为90%，意味着有90%的可能性（）。

    • A、估计值等于总体的实际平均值
    • B、实际总体平均值不大于最大的间距结束点
    • C、总体平均值的标准差不大于10%
    • D、总体平均值落在特定的置信区间内

    正确答案:D

  • 第20题：

    单选题
    总体均值的置信水平为90%，意味着有90%的可能性（）。
    A

    估计值等于总体的实际平均值

    B

    实际总体平均值不大于最大的间距结束点

    C

    总体平均值的标准差不大于10%

    D

    总体平均值落在特定的置信区间内


    正确答案： D
    解析： D这是对置信区间的定义。选项A不正确，置信区间只是考虑总体参数是否包含在间距中，和参数的具体值无关。选项B不正确，如果置信区间是单边的，这可能是正确的，但对更普通的双边置信区间，则是不正确的。它在90%的置信区间超过间距上限的正确几率是5%。选项C不正确，置信区间建立在标准差的基础上，但是和标准差的大小无关。

  • 第21题：

    多选题
    已知正态总体标准差为10，样本量n=25，置信水平为95%，Z=1.96，样本均值=105.36。则以下正确的有（）
    A

    样本均值的标准差为10

    B

    样本均值的标准差为2

    C

    样本均值的置信区间为（101.44，109.28）

    D

    总体均值的置信区间为（101.44，109.28）


    正确答案： D,C
    解析： 暂无解析

  • 第22题：

    多选题
    使用同一组样本根据正态分布估计总体均值时，如果将置信度由95%调整为90%，则（　　）。[2014年初级真题]
    A

    zα/2将增大

    B

    zα/2将减小

    C

    样本均值保持不变

    D

    置信区间宽度减小

    E

    置信区间宽度增加


    正确答案： D,A
    解析：
    zα/2为标准正态分布的α/2左分位数，随α的增大而减小，置信度由95%调整为90%时，α由0.05增大为0.1，zα/2减小。样本均值不受置信度变化的影响。置信度降低，说明置信区间的准确性降低，置信区间的宽度减小。

  • 第23题：

    单选题
    正态均值的90%的置信区间是从13.8067至18.1933。这个意思是：（）
    A

    均值落在13.8067至18.1933范围内的概率是90%

    B

    总体中所有值的90%落在13.8067至18.1933

    C

    总体中所有样本值的90%落在13.867至13.1933

    D

    置信区间变差均值的概率为90%


    正确答案： B
    解析： 暂无解析

  • 第24题：

    填空题
    根据一个具体的样本求出的总体均值90%的置信区间（）

    正确答案： 以90%的概率包含总体均值
    解析： 暂无解析

相关内容