单选题多边形闭合导线其内角和的理论值为（n－2）×180°，式中的n代表（）。A 方向数；B 内角数；C 边数；D 观测数。

题目
单选题
多边形闭合导线其内角和的理论值为（n－2）×180°，式中的n代表（）。
A

方向数；

B

内角数；

C

边数；

D

观测数。

相似考题

1.闭合导线各边纵横坐标增量的代数和的理论值∑Δχ理和∑Δχ理应为()的数。A、>0B、闭合导线各边纵横坐标增量的代数和的理论值∑Δχ理和∑Δχ理应为()的数。A、>0B、C、等于零D、不等于零

2.若两个多边形的边数相差1，则它们的内角和、外角和分别有多少异同？

3.一个凸多边形内角和是1080度，这个多边形的边数是（ ）A．5B．6C．7D．8

4.多边形内角和等于( )A..(n－2)×0°；B..(n－2)×90°；C..(n－2)×180°；D..(n－2)×360°

参考答案和解析
正确答案： D
解析： 暂无解析
更多“单选题多边形闭合导线其内角和的理论值为（n－2）×180°，式中的n代表（）。A 方向数；B 内角数；C 边数；D 观测数。”相关问题

  • 第1题：

    一个多边形的内角和比它的外角的和的2倍还大180°，这个多边形的边数是（ ）

    A.5 B.6 C.7 D.8


    正确答案：C
    C.点拨：据题意，得（n－2）·180＝2×360+180.解得n＝7.故选C；

  • 第2题：

    n边形各内角观测值中误差均为±6"，则内角和的中误差为：


    答案：B
    解析：
    提示：内角和=(n-2) X180°，用误差传播定律计算。

  • 第3题：

    已知n边形各内角观测值中误差均为±6″，则内角和的中误差为( )。

    A.±6″n
    B.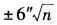
    C.±6″/n
    D.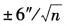

    答案：B
    解析：

  • 第4题：

    多边形闭合导线其内角和的理论值为（n－2）×180°，式中的n代表（）。

    • A、方向数；
    • B、内角数；
    • C、边数；
    • D、观测数。

    正确答案:B

  • 第5题：

    某闭合导线，观测的内角分别是β1β2β3β4，其角度闭合差fβ为（）

    • A、Σβ-（n-2）·180
    • B、Σβ-（n+2）·180
    • C、（n-2）·180

    正确答案:A

  • 第6题：

    洞类导线宜沿中线布设成多边形闭合导线，其闭合环边数应小于（）条。

    • A、5
    • B、6
    • C、7

    正确答案:C

  • 第7题：

    闭合导线测量中，实际观测所得的内角总和不等于其理论总和，其相差的数值称为闭合导线的（）。


    正确答案:角度闭合差

  • 第8题：

    闭合导线角度闭合差指的是（）

    • A、多边形内角观测值之和与理论值之差
    • B、多边形内角和理论值与观测值和之差
    • C、多边形内角观测值与理论值之差
    • D、多边形内角理论值与观测值之差

    正确答案:A

  • 第9题：

    闭合导线的角度闭合差等于该导线构成的多边形的内角和


    正确答案:错误

  • 第10题：

    判断题
    闭合导线的角度闭合差等于该导线构成的多边形的内角和
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第11题：

    单选题
    某导线网中，观测角数20，观测边数17，总点数Z=14，必要起算数据B=3，则必要观测数为（）。
    A

    20

    B

    25

    C

    28

    D

    31


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    某闭合导线，观测的内角分别是β1β2β3β4，其角度闭合差fβ为（）
    A

    Σβ-（n-2）·180

    B

    Σβ-（n+2）·180

    C

    （n-2）·180


    正确答案： B
    解析： 暂无解析

  • 第13题：

    一个多边形的每一个内角都相等，且比它的一个外角大100°，则边数n＝_____.


    正确答案：
    9

  • 第14题：

    在“多边形内角和”一课上，某教师设计如下的教学过程：
    一、学生自主学习，通过阅读课本理解多边形的定义及相关概念
    1．多边形的定义：在平面内，由若干条不在同一直线上的线段首尾顺次相连组成的封闭图形叫做多边形。在定义中应注意：①若干条；②首尾顺次相连，二者缺一不可。
    2．多边形的分类：有凸多边形和凹多边形之分。
    3．多边形的相关概念：边、内角、顶点、对角线、内角和的含义与三角形相同。
    4．多边形的命名和表示：通常以边数命名，多边形有n条边就叫做／l,边形。三角形、四边形都属于多边形，其中三角形是边数最少的多边形。多边形的表示方法与三角形、四边形类似。可以用表示它的顶点的字母来表示，可顺时针方向表示，也可逆时针方向表示。
    二、探索多边形的内角和的公式(见活动探究卡)
    在了解了多边形的有关概念后，我们重点来研究和探索多边形的内角和的公式。
    活动探究要求：请以小组为单位，利用活动探究卡与同伴合作探索多边形的内角和。
    活动：从多边形的一个顶点引对角线来探索多边形的内角和
    边数 从某顶点出发的对角线条数划分成的三角形个数 多边形的内角和 计算规律
    3
    4
    5
    6
    7
    8
    结论：④从n边形的一个顶点出发可以引条对角线，把H边形分成个三
    角形，每个三角形的内角和 ②n边形的内角和公式： (n>3)(学生讨论、画图、猜想、归纳自己的方法，并请小组的中心发言人在全班进行交流展,教师利用课件演示，师生共同得到结论)
    教师小结：在求多边形的内角和时，先把多边形转化成三角形，进而求出内角和．这种由未知转化为已知的方法是我们数学中一种非常重要的方法。
    阅读上述教学设计片段，完成下列任务：
    (1)本节课的教学目标是什么 (8分)
    (2)本节课的教学重难点是什么 (8分)
    (3)请为此教学片段设计一个导入过程。(14分)


    答案：
    解析：
    (1)知识与技能：①掌握多边形的概念；②探索并理解多边形的内角和公式；③会用多边形的内角和公式进行计算。
    过程与方法：①经历探索多边形内角和公式的过程，提升合情推理意识，主动探究的习惯，进一步体会数学与现实生活的紧密联系；②探索并了解多边形的内角和公式，培养说理和简单推理的意识及能力。
    情感、态度与价值观：①经历探索多边形内角和的过程，通过师生共同活动，训练学生的发散性思维．培养学生的创新精神；②进一步发展学生合情推理意识、主动探究习惯，进一步体会数学与现实生活的紧密联系。
    (2)教学重点：多边形的内角和公式的探索、归纳及运用公式进行有关计算。
    教学难点：如何引导学生参与到探索多边形的内角和公式过程中，通过动手实践、观察分析、归纳总结得出多边形的内角和公式。
    (3)导入环节：
    工人师傅将一个四边形的桌面用锯子锯掉一个角，剩余的木板会出现什么形状的图形，还剩几个角 内角和是多少
    (学生思考、讨论、回答；教师利用课件演示三种情况。得出结论：三角形，四边形，五边形)如何知道五边形的内角和呢
    这就是本节课我们需要学习的主要内容：
    教师板书课题：4．6探索多边形的内角和(一)
    并利用课件展示本节课的学习目标，教师导读，学生理解。

  • 第15题：

    多边形内角和等于（）。

    • A、（n－2）×0°；
    • B、（n－2）×90°；
    • C、（n－2）×180°；
    • D、（n－2）×360°。

    正确答案:C

  • 第16题：

    某导线网中，观测角数20，观测边数17，总点数Z=14，必要起算数据B=3，则必要观测数为（）。

    • A、20
    • B、25
    • C、28
    • D、31

    正确答案:B

  • 第17题：

    洞内导线宜沿中线布设成多边形闭合导线，其闭合环边数应小于（）条。

    • A、5
    • B、6
    • C、7

    正确答案:C

  • 第18题：

    在闭合导线中角度的计算中，闭合多边形内角的理论值为（n-2）×180°，但由于测角有误差，实测内角总和与理论值不符，两者之差叫角度闭合差。


    正确答案:正确

  • 第19题：

    六边形闭合导线，其内角和理论值应为（）

    • A、360°
    • B、540°
    • C、720°
    • D、900°

    正确答案:C

  • 第20题：

    n边形闭合导线内角和的理论值为（）

    • A、（n-2）180°
    • B、（n-3）180°
    • C、（n-2）360°
    • D、（n-3）360°

    正确答案:A

  • 第21题：

    附合导线的角度闭合差等于导线起始边与终结边坐标方位角之差加上全部转折角之和再减去（）与180°乘积。

    • A、边长
    • B、折角数
    • C、边数
    • D、边数允许值

    正确答案:B

  • 第22题：

    单选题
    多边形内角和等于（）。
    A

    （n－2）×0°；

    B

    （n－2）×90°；

    C

    （n－2）×180°；

    D

    （n－2）×360°。


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    多边形闭合导线其内角和的理论值为（n－2）×180°，式中的n代表（）。
    A

    方向数；

    B

    内角数；

    C

    边数；

    D

    观测数。


    正确答案： D
    解析： 暂无解析

  • 第24题：

    单选题
    附合导线的角度闭合差等于导线起始边与终结边坐标方位角之差加上全部转折角之和再减去（）与180°乘积。
    A

    边长

    B

    折角数

    C

    边数

    D

    边数允许值


    正确答案： C
    解析： 暂无解析

相关内容