单选题设总体X服从正态分布N（μ，9），1225X，X，L，X是来自该总体的简单随机样本，对检验问题00H：μ=μ，11H：μ=μ，取如下拒绝域：0{x−μ≥c}。若取置信水平等于0.95，则当01μ=0，μ=2时，犯第二类错误的概率为（）。A Φ（−1.37）−Φ（−5.29）B Φ（1.176）−Φ（1.96）C Φ（1.96）−Φ（−1.96）D Φ（1.96）−Φ（0）E Φ（0）−Φ（−1.96）

题目

单选题

设总体X服从正态分布N（μ，9），1225X，X，L，X是来自该总体的简单随机样本，对检验问题00H：μ=μ，11H：μ=μ，取如下拒绝域：0{x−μ≥c}。若取置信水平等于0.95，则当01μ=0，μ=2时，犯第二类错误的概率为（）。

Φ（−1.37）−Φ（−5.29）

Φ（1.176）−Φ（1.96）

Φ（1.96）−Φ（−1.96）

Φ（1.96）−Φ（0）

Φ（0）−Φ（−1.96）

相似考题

1.对于均数为μ、标准差为σ的正态分布，95％的变量值分布范围为A、（μ－σ）～（μ+σ）B、（μ－1.96σ）～（μ+1.96σ）C、（μ－2.58σ）～（μ+2.58σ）D、－∞～（μ+1.96σ）E、0～（μ+1.96σ）

2.已知Y~N(μ·σ),则Y在区间[μ－1.96σ,μ＋1.96σ]的概率为A.0.95B.0.05C.0.01SXB已知Y～N（μ·σ），则Y在区间［μ-1.96σ，μ+1.96σ］的概率为A.0.95B.0.05C.0.01D.0.99E.0.90

3.当样本含量足够大，总体阳性率与阴性率均不接近于0和1，总体率95％可信区间的估计公式为A．P±2．58SpB．P±1．96SpC．P±1．96SxD．P±2．58SxE．X±1．96Sx

4.原始数据呈近似正态分布时，下列可用于估计其95％参考值范围的公式是A.X±t0．o5+uSB.X±1．96SC.X±2．58SD.X±t0．o5+vSxE.X±1．96Sx

更多“单选题设总体X服从正态分布N（μ，9），1225X，X，L，X是来自该总体的简单随机样本，对检验问题00H：μ=μ，11H：μ=μ，取如下拒绝域：0{x−μ≥c}。若取置信水平等于0.95，则当01μ=0，μ=2时，犯第二类错误的概率为（）。A Φ（−1.37）−Φ（−5.29）B Φ（1.176）−Φ（1.96）C Φ（1.96）−Φ（−1.96）D Φ（1.96）−Φ（0）E Φ（0）−Φ（−1.96）”相关问题

第1题：

在参数未知的正态总体中随机抽样(n>100)，IX-uI≥下列哪项的概率为5％
A.1.96a
B.t0．o5S
C.1．96Sg
D.1．645Sx
E.u0．o5o

正确答案：C
第2题：

在正态分布下，Z= -1.96到Z=1.96之间的概率为()

A.0. 475
B.0.01
C.0. 95
D.0.05

答案：C
解析：
推断统计；推断统计的数学基础。 ±1个标准差之间包含所有数据的68.26%；±1.96个标准差之间包含所有数据的95%；±2.58个标准差之间包含所有数据的99%。所以答案为C。
第3题：

当样本量足够大时，总体阳性率与阴性率均不接近于0和1，总体率95%的可信区间的估计公式为

A.P±2.58S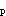
B.P±1.96S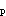
C.P±1.96S
D.P±2.58S
E.X±1.96S

答案：B
解析：
当样本含量n足够大，阳性率与阴性率均不接近于0和1，样本率的分布近似正态分布，总体率可信区间总体率95%的可信区间：P±1.96S。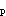
第4题：

设从正态分布的总体N(μ，σ2)中进行随机抽样，样本含量n的大小相等，其样本均数为x朋从均数为μ，方差为σx2，当σ已知时，由μ分布(标准正态分布)可知，正态曲线下有95%的μ值满足下式：-1.96≤μ≤+1.96，则总体均数μ的95%置信区间为( )。

A.[x-l.96σx，x+l.96σ2]
B.[x-1.96μ，0]
C.[μ-l.96μx，μ+l.96σx]
D.[O，x+l.96σ2]
E.[x-l.96，x+l.96]

答案：A
解析：
第5题：

当样本含量足够大，总体阳性率与阴性率均不接近0和1，总体率95%可信区间的估计公式为

A.P±2.58S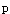
B.P±1.96S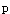
C.P±1.96S
D.P±2.58S
E.X±1.96S

答案：B
解析：
第6题：

已知随机误差服从N（0，б²）分布，随机误差在（－1.96σ，1.96σ）区间内的概率是（）。
- A、90%
- B、95%
- C、97.5%
- D、99%
正确答案:B
第7题：

若X服从正态分布N（μ，σ²），则X的第95百分位数即（）
- A、μ－1.645σ
- B、μ－1.96σ
- C、μ＋1.96σ
- D、μ＋1.645σ
正确答案:D
第8题：

当总体为非正态时，计算双侧95%医学参考值范围的公式为（）
- A、X±1.96S
- B、p2.5-p97.5
- C、p25-p75
- D、p±1.96p
- E、X±1.96S_x
正确答案:B
第9题：

当样本含量足够大时，样本率又不接近0或1时，以样本率推断总体率95%可信区间的计算公式为（）
- A、p±2.58s_P
- B、p+1.645s_P
- C、p±1.96s_P
- D、π±1.96σ_π
- E、X±1.96s_X
正确答案:C
第10题：

对于正态分布资料，可用于估计99%的参考值范围的是（）。
- A、（μ-σ）～（μ+σ）
- B、（μ-1.96σ）～（μ+1.96σ）
- C、（μ-2.58σ）～（μ+2.58σ）
- D、-∞～（μ+1.96σ）
- E、0～（μ+1.96σ）
正确答案:C
第11题：

单选题
设总体X服从正态分布N（μ，9），1225X，X，L，X是来自该总体的简单随机样本，对检验问题00H：μ=μ，11H：μ=μ，取如下拒绝域：0{x−μ≥c}。若取置信水平等于0.95，则当01μ=0，μ=2时，犯第二类错误的概率为（）。
A
Φ（−1.37）−Φ（−5.29）
B
Φ（1.176）−Φ（1.96）
C
Φ（1.96）−Φ（−1.96）
D
Φ（1.96）−Φ（0）
E
Φ（0）−Φ（−1.96）

正确答案： B
解析：暂无解析
第12题：

单选题
对于均数为μ、标准差为σ的正态分布，95％的变量值分布范围为（）
A
（μ－σ）～（μ+σ）
B
（μ－1.96σ）～（μ+1.96σ）
C
（μ－2.58σ）～（μ+2.58σ）
D
－∞～（μ+1.96σ）
E
0～（μ+1.96σ）

正确答案： A
解析：暂无解析
第13题：

若x值的均数等于7,标准差等于2,则x＋3的均数A.也等于7B.等于9C.等于l0

若x值的均数等于7，标准差等于2，则x+3的均数
A.也等于7
B.等于9
C.等于l0
D.界于7—3与7+3之间
E.界于7—1．96×2与7+1．96×2之间

正确答案：C
略
第14题：

当样本含量足够大时，样本率又不接近0或1时，以样本率推断总体率95%可信区间的计算公式为

A.p+1．645s
B.π±1．96σ
C.p±2．58s
D.X±1．96s
E.p±1．96s

答案：E
解析：
第15题：

当样本量足够大时，总体阳性率与阴性率均不接近于0和1，总体率95％的可信区间的估计公式为（）
A.P±2．58 Sp
B.P±1．96 Sp
C.P±1．96 Sx
D.P±2．58 Sx
E.X±1．96 Sx

答案：B
解析：
第16题：

对于一组正态分布的资料，样本含量为n，样本均数为X，标准差为S，该资料的总体均数可信区间为

A.X±1.96S
B.X±tS
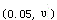C.X±tS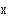
D.P2.5～P97.5
E.lg-1(X±1.96S)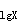

答案：C
解析：
第17题：

已知随机误差服从N（0，σ²）分布，随机误差落在（-1.96σ，1.96σ）区间内的概率是（），（-3σ，3σ）区间内的概率是（）。
- A、0.95
- B、0.975
- C、0.997
- D、0.90
正确答案:A,C
第18题：

假设检验中,H₀:μ≥μ₀，H₁:μ<μ₀<0,N为大样本,统计量Z=(x-μ₀)/σ,α=0.05,拒绝域为：（）
- A、Z<-1.96
- B、Z>1.96
- C、Z>1.65
- D、Z<-1.65
正确答案:D
第19题：

设总体X服从正态分布N（μ，9），1225X，X，L，X是来自该总体的简单随机样本，对检验问题00H：μ=μ，11H：μ=μ，取如下拒绝域：0{x−μ≥c}。若取置信水平等于0.95，则当01μ=0，μ=2时，犯第二类错误的概率为（）。
- A、Φ（−1.37）−Φ（−5.29）
- B、Φ（1.176）−Φ（1.96）
- C、Φ（1.96）−Φ（−1.96）
- D、Φ（1.96）−Φ（0）
- E、Φ（0）−Φ（−1.96）
正确答案:A
第20题：

某随机变量从标准正态分布N（0，1），则此随机变量落入（-1.96，1.96）区间内的概率为（）。
- A、95%
- B、99%
- C、095
- D、0.99
正确答案:A
第21题：

当样本含量足够大，总体阳性率与阴性率均不接近0和1，总体率95%可信区间的估计公式为（）
- A、P±2.58Sp
- B、P±1.96Sp
- C、P±1.96Sx
- D、P±2.58Sx
- E、X±1.96Sx
正确答案:B
第22题：

单选题
对于正态分布资料，可用于估计99%的参考值范围的是（）。
A
（μ-σ）～（μ+σ）
B
（μ-1.96σ）～（μ+1.96σ）
C
（μ-2.58σ）～（μ+2.58σ）
D
-∞～（μ+1.96σ）
E
0～（μ+1.96σ）

正确答案： A
解析：暂无解析
第23题：

单选题
假设检验中,H0:μ≥μ0，H1:μ00)/σ,α=0.05,拒绝域为：（）
A
Z<-1.96
B
Z>1.96
C
Z>1.65
D
Z<-1.65

正确答案： A
解析：暂无解析
第24题：

单选题
若X服从正态分布N（μ，σ2），则X的第95百分位数即（）
A
μ－1.645σ
B
μ－1.96σ
C
μ＋1.96σ
D
μ＋1.645σ

正确答案： C
解析：暂无解析

题目

相似考题

相关内容